GRADE
12
Advanced Functions MHF4U
More homework, harder tests, and tough assignments, tutoring is all about an individualized plan that builds the academic skills, good habits and positive attitudes needed to succeed in high school and beyond.
This course extends students' experience with functions. Students will investigate the properties of polynomial, rational, logarithmic, and trigonometric functions; develop techniques for combining functions; broaden their understanding of rates of change; and develop facility in applying these concepts and skills. Students will also refine their use of the mathematical processes necessary for success in senior mathematics. This course is intended both for students taking the Calculus and Vectors course as a prerequisite for a university program and for those wishing to consolidate their understanding of mathematics before proceeding to any one of a variety of university programs. Prerequisite: Grade 11 Functions and Relations MCR3U
This course extends students' experience with functions. Students will investigate the properties of polynomial, rational, logarithmic, and trigonometric functions; develop techniques for combining functions; broaden their understanding of rates of change; and develop facility in applying these concepts and skills. Students will also refine their use of the mathematical processes necessary for success in senior mathematics. This course is intended both for students taking the Calculus and Vectors course as a prerequisite for a university program and for those wishing to consolidate their understanding of mathematics before proceeding to any one of a variety of university programs. Prerequisite: Grade 11 Functions and Relations MCR3U
TABLE OF CONTENTS
Functions
The Vertical Line Test
All functions must 'pass' the vertical line test with one value of y for each value of x.
Solution
Functions cannot have two values of y for one value of x. A vertical line drawn anywhere through a function will never cross a function twice.
Graphs of Functions: Even and Odd Functions
Determine whether the function is even, odd, or neither by comparing ƒ(x), ƒ(-x), and -ƒ(x).
Solution
Even Odd
Show algebraically whether the function is even:
Solution
All functions are even when
ƒ(x) = ƒ(-x)
Substitute and see if above ^ is true...
Comparing the factored forms, the two functions are not equivalent. Since ƒ(x) ≠ ƒ(-x), then the function is NOT even.
Show algebraically whether the function is odd:
Solution
All functions are odd when
ƒ(-x) = -ƒ(x)
Substitute and see if above ^ is true...
Since ƒ(-x) ≠ -ƒ(x), then the function is NOT odd.
End Behaviour
The end behaviour is what happens to y when x approaches positive infinity (+∞) or approaches negative infinity (-∞).
The end behaviour is the same for the two functions:
Solution
ƒ(x) = -5x9 + 3x4 + 2x3
ƒ(x) = -5x9
The end behaviour depends only on the one term with the highest degree.
As x approaches positive infinity, y approaches negative infinity.
As x approaches negative infinity, y approaches positive infinity.
As x approaches positive infinity, y approaches negative infinity.
As x approaches negative infinity, y approaches positive infinity.
Determine the end behaviour of the function: ƒ(x) = -5x9 + 3x4 + 2x3
Solution
To determine the behaviour as x → -∞, try substituting a large/negative x-value (like -100) and see if y → +∞ or y → -∞.
To determine the behaviour as x → +∞, try substituting a large/positive x-value (like 100) and see if y → +∞ or y → -∞.
Determine which function has the end behaviour:
Solution
As x → +∞, y → -∞
As x → -∞, y → -∞
To determine end behaviour try substituting large positive, and large negative values of x into the functions to see if y approaches +∞ or -∞.
Which end behaviour rule is incorrect? Solution
| Function is: | As x → -∞ | As x → +∞ | |
| A | Positive, Even | y → +∞ | y → +∞ |
| B | Positive, Odd | y → -∞ | y → +∞ |
| C | Negative, Even | y → -∞ | y → -∞ |
| D | Negative, Odd | y → +∞ | y → +∞ |
For an odd function: ƒ(-x) = -ƒ(x)
As x → -∞, y → -∞
As x → +∞, y → -∞
As x → -∞, y → -∞
As x → +∞, y → -∞
Sketching graphs: Zeros, End Behaviour, and Turning Points (Stationary Points)
Given the function,
ƒ(x) = (3x2 + 8x + 4)(x2 - 9)State the x-values of the zeros (x-intercepts), from lowest to highest.
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Zeros (x-intercepts) are: -3, -2, -2/3, and 3
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
State the end behaviours.
Solution
Use the term with the highest degree, which will come from...
Then determine the output values for ƒ(-∞) and ƒ(+∞)...
And,
The y-intercept occurs at:
Solution
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The y-intercept always occurs when x = 0... So find ƒ(0)...
At the point (0, -36)... y = -36
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Determine the number of turning points.
Solution
# =
Hint
Clear
Info
Incorrect Attempts:
CHECK
turning points
Hint Unavailable
# =
Hint
Clear
Info
Incorrect Attempts:
CHECK
turning points
Hint Unavailable
Set and Interval Notation
Write each of the following as the other form... in either set notation or interval notation. Remember that interval notation uses parentheses ( ) for less than (<) or greater than (>), and square brackets [ ] is used for greater than or equal to [≥], and less than or equal to [≤].
±∞ ... uses ... ( )
>, < ... uses ... ( )
≥, ≤ ... uses ... [ ]
You will need some of the symbols below, provided for your copy-paste convenience.
∞ ≤ ≥ < >
Write {XER | x ≥ -4} in interval notation.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Write {YER | 23 < y ≤ 67} in interval notation.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Write ( 0, 4 ] in set notation in the form {XER | ______ }.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Domain and Range
Select the incorrect statement.
Solution
The set of all real inputs is the domain.
The set of all real outputs is the range.
The set of all real outputs is the range.
Parent Function Features
Sort the parent functions into their defining features:
Solution
y-intercept at (0,1)
Domain: {XER | x ≥ 0}
End behaviour: x → -∞, y → +∞
Has both vertical and horizontal asymptotes
- : End behaviour: x → -∞, y → +∞
- : Domain: {XER | x ≥ 0}
- : y-intercept at (0,1)
- : Has both vertical and horizontal asymptotes
y-intercept at (0,1)
Domain: {XER | x ≥ 0}
End behaviour: x → -∞, y → +∞
Has both vertical and horizontal asymptotes
- : End behaviour: x → -∞, y → +∞
- : Domain: {XER | x ≥ 0}
- : y-intercept at (0,1)
- : Has both vertical and horizontal asymptotes
Factoring polynomials
Factor the general quadratic equation.
Solution
abx2 + (an + bc)x + cn
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Factoring: Difference of Squares and Fractions
Factor fully.
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
y = x4 - y2
y = (x2)2 - (y)2
y = (x2 + y)(x2 - y)
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
y = (x2)2 - (y)2
y = (x2 + y)(x2 - y)
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
y = 25x4 - 9y2
y = (5x2)2 - (3y)2
y = (5x2 + 3y)(5x2 - 3y)
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
y = (5x2)2 - (3y)2
y = (5x2 + 3y)(5x2 - 3y)
Inverse Functions
The inverse of which of the following is not a function?
Solution
The inverse of a quadratic function is not a function because it does not pass the vertical line test (i.e. it has two different values of y for the same value of x).
Inverse Functions
Determine the equation of the inverse of the quadratic function:
Solution
y = x2 - 6x - 24
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Complete the Square
Converting to vertex form by completing the square would yield which of the following?
Solution
Video
y = ax2 + bx + c
Based on this work, determine the equation for the axis of symmetry.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The equation of the axis of symmetry is the x-value of the vertex...
Interestingly (as an aside) this is the equation of the max or min value...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Transformations with Function Notation
Which function is vertically compressed by a factor of ½, and translated 2 units right?
Solution
For the function:
y = a ƒ (k (x - d) ) + c
When |a| > 0, the function is vertically compressed by a factor of 'a'.
When d > 0, the function is translated 'd' units right.
y = a ƒ (k (x - d) ) + c
When |a| > 0, the function is vertically compressed by a factor of 'a'.
When d > 0, the function is translated 'd' units right.
Piecewise and Continuity
Given the piecewise function,
The function is continuous.
Solution
From a quick observation or sketch, you will see that the piecewise function is not continuous, at x = 1.
State the domain and range, using proper set notation with curly braces { }, and pipe |, like for example {XER | x > 5}.
Solution
Hint
Clear
Info
Domain:
Range:
Incorrect Attempts:
CHECK
Hint Unavailable
Domain: {XER}
Range: {YER | y < 5}
For the range, think about (or sketch) the greatest value of 'y' for each function in the piecewise notation. For ƒ(x) = 4x + 1, {XER | x < 1} you should see that the maximum 'y' value is 'less than' 5.
And of course for the function, ƒ(x) = 3, the maximum value of 'y' is 3 everywhere.
So putting this together the range of 'y' is everything less than 5, so it is {YER | y < 5}...
Hint
Clear
Info
Domain:
Range:
Range:
Incorrect Attempts:
CHECK
Hint Unavailable
Range: {YER | y < 5}
For the range, think about (or sketch) the greatest value of 'y' for each function in the piecewise notation. For ƒ(x) = 4x + 1, {XER | x < 1} you should see that the maximum 'y' value is 'less than' 5.
And of course for the function, ƒ(x) = 3, the maximum value of 'y' is 3 everywhere.
So putting this together the range of 'y' is everything less than 5, so it is {YER | y < 5}...
Polynomial Functions
| Specific Topic | General Topic | School | Date |
|---|---|---|---|
| Solving a Volume Word Problem | Factoring Polynomials | North Toronto | Sep 2013 |
Intro to Polynomial Functions
The domain of a polynomial is always xεR, while the range has various bounds.
Solution
The domain can have various restrictions, or inequalities on it, and is not always just xεR.
Intro to Polynomial Functions
Which of the following is considered a polynomial function?
Solution
A polynomial cannot have:
• Negative exponents like 2x-3, or .
• Non-integer degrees like .
• Coefficients that aren't real numbers like
• Negative exponents like 2x-3, or .
• Non-integer degrees like .
• Coefficients that aren't real numbers like
Real and Unreal (Imaginary, Complex Number) Roots of Polynomial Functions
The degree of a polynomial equals the number of real plus unreal roots. This rule does not work well for linear polynomials. Anyways, determine the number of roots in each...
Degree = Real Roots + Unreal RootsFor quadratic (U-shaped) polynomials.
Solution
2 real roots
2 real, equal roots
2 unreal roots
Drag each, to reveal correct answer.
2 real roots
2 real, equal roots
2 unreal roots
For cubic (S-shaped) polynomials.
Solution
3 real/equal roots
1 real root, and 2 real/equal roots
3 real roots
1 real root, and 2 unreal roots
Drag each, to reveal correct answer.
3 real/equal roots
1 real root, and 2 real/equal roots
3 real roots
1 real root, and 2 unreal roots
For quartic (U or W-shaped) polynomials. (Some categories will apply to more than one graph)
Solution
4 real/equal roots
4 real roots
4 unreal roots
4 real roots (2 equal sets)
Drag each, to reveal correct answer.
4 real/equal roots
4 real roots
4 unreal roots
4 real roots (2 equal sets)
For more quartic (U or W-shaped) polynomials. (Some categories will apply to more than one graph)
Solution
2 real, and 2 unreal roots
2 real/equal, and 2 unreal roots
2 equal/real roots, and 2 other real roots
3 equal/real roots, and 1 real root
Drag each, to reveal correct answer.
2 real, and 2 unreal roots
2 real/equal, and 2 unreal roots
2 equal/real roots, and 2 other real roots
3 equal/real roots, and 1 real root
Finite Differences of a Polynomial
Use finite differences to determine the nature of the function. Solution
| x | y |
| -3 | -88 |
| -2 | -29 |
| -1 | -6 |
| 0 | -1 |
| 1 | 4 |
| 2 | 27 |
| 3 | 86 |
The same number for 3rd differences is a cubic function, like x3...


Polynomial Functions and Finite Difference
Given the following formula for finite differences of a polynomial, where 'n' is the degree of the function,
Finite Difference = (Leading Coefficient) × (n!)The polynomial, will have fifth differences the same.
Solution
Finite Difference = (Leading Coefficient) × (n!)
The 5th differences would take a long time to calculate, but it is done with the y-values of consecutive x-values...
The nth differences are the same for the nth degree. Where n = 5
The nth differences are the same for the nth degree. Where n = 5
If the 3rd finite differences of a different function are constant, with a difference of -12, then determine the value of the leading coefficient.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Remember
Finite Difference = (Leading Coefficient) × (n!)
If the 3rd finite differences of a different function are constant then the degree of the function is 3, so n = 3, and the given finite difference = -12...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Polynomial Function Properties
Polynomial functions never have vertical or horizontal asymptotes.
Solution
Rational functions have vertical and horizontal asymptotes,
Since rational functions are not polynomial functions, then polynomial functions never have vertical or horizontal asymptotes.
Symmetry of Polynomial Functions
Which of the following functions is neither even nor odd (referring to the degree)?
Solution
The rule for determining even and odd functions:
Even: ƒ(x) = ƒ(-x)
Odd: ƒ(-x) = -ƒ(x)
The following functions will do this because they only one even degree, which will cancel the negative sign, ƒ(x) = ƒ(-x):
∴ a) and c) are even.
Check c)
∴ is odd.
Check d)
The different magnitudes 4, and 2 would not work with the other ƒ(-x) = -ƒ(x) either,
∴ is neither.
Odd: ƒ(-x) = -ƒ(x) The following functions will do this because they only one even degree, which will cancel the negative sign, ƒ(x) = ƒ(-x):
∴ a) and c) are even.
Check c) ∴ is odd.
Check d) The different magnitudes 4, and 2 would not work with the other ƒ(-x) = -ƒ(x) either,
∴ is neither.
Given the information in the table below, determine the nature of the function. Solution
| x | ƒ(x) |
| 4 | 664 |
| 3 | 33 |
| -2 | -23 |
| -4 | -74 |
| -5 | -43 |
A function is even when: ƒ(-x) = ƒ(x).
A function is odd when: ƒ(-x) = -ƒ(x).
Use the points (4, 664) and (-4, -74)
ƒ(+4) = -644, ƒ(-4) = -74
∴ Not even, and not odd.
A function is odd when: ƒ(-x) = -ƒ(x).
Use the points (4, 664) and (-4, -74)
ƒ(+4) = -644, ƒ(-4) = -74
∴ Not even, and not odd.
Determine the properties of the polynomial function...
Solution
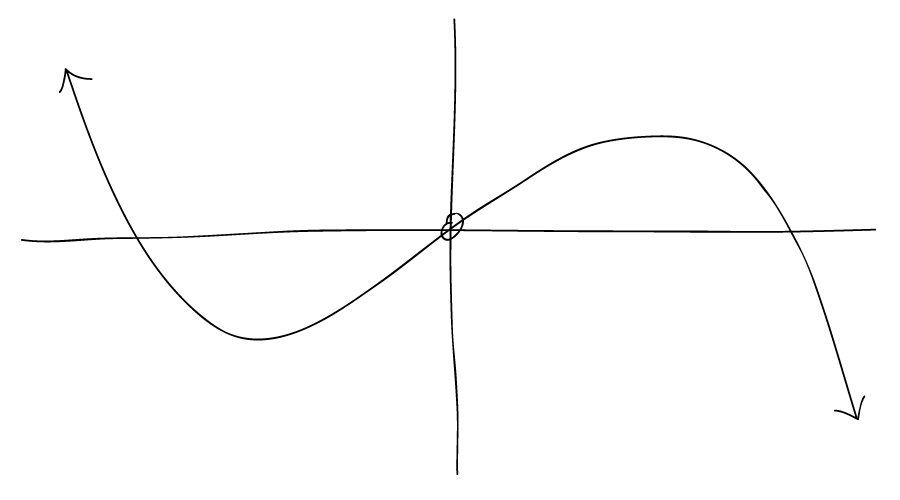
- If the function has symmetry on the vertical (y) axis, then it has an even degree. (But not all even-degree functions have vertical symmetry).
- If the function has rotational symmetry about the origin or some other point, then it has an odd degree. (But not all odd-degree functions have rotational symmetry).
- Most even-degree functions (as compared to odd-degree functions) have end behaviours on the same side of the x-axis.
- Odd functions are either quadrant 2 & 4, or 1 & 3
- Quadrant 2 & 4 is negative leading coefficient.
- Quadrant 1 & 3 is positive leading coefficient.
- If the function has symmetry on the vertical (y) axis, then it has an even degree. (But not all even-degree functions have vertical symmetry).
- If the function has rotational symmetry about the origin or some other point, then it has an odd degree. (But not all odd-degree functions have rotational symmetry).
- Most even-degree functions (as compared to odd-degree functions) have end behaviours on the same side of the x-axis.
- Odd functions are either quadrant 2 & 4, or 1 & 3
- Quadrant 2 & 4 is negative leading coefficient.
- Quadrant 1 & 3 is positive leading coefficient.
Check the three correct properties of the polynomial function...
Solution

- Even degree (because has line symmetry)
- Negative leading coefficient (because even in quadrant 3 & 4)
- Line symmetry (mirror image across the y-axis)
- Even degree (because has line symmetry)
- Negative leading coefficient (because even in quadrant 3 & 4)
- Line symmetry (mirror image across the y-axis)
Check the two correct properties of the polynomial function, and state the factors, in your notes.
Solution

- Odd degree, minimum degree of 5 (one more than the number of turning points)
- Negative leading coefficient (because odd in quadrant 2 & 4)
- Factors: (x + 3)(x + 1)(x)2(x - 4)
In the factors, it's (x)2 because the curve 'bounces' at this point, rather than goes straight through.
- Odd degree, minimum degree of 5 (one more than the number of turning points)
- Negative leading coefficient (because odd in quadrant 2 & 4)
- Factors: (x + 3)(x + 1)(x)2(x - 4)
Characteristics of Functions
Which of the following functions has no zeros, one turning point, and an even degree?
Solution
Quadratics with x2 have only 1 turning point (because the maximum number of turning points in a function equals the degree - 1).
This leaves only B) and D) as possible options.
You could try to factor but when you see neither quadratic is factorable, you could use the quadratic formula to determine the zeros. Furthermore, a function has no zeros/real roots/x-intercepts when the value of the discriminant (b2 - 4ac) is negative.
Try D) a=-2, b=4, c=10
Try B) a=1, b=5, c=12
∴ Since the discriminant is negative in B), it will not have any real roots.
This leaves only B) and D) as possible options.
You could try to factor but when you see neither quadratic is factorable, you could use the quadratic formula to determine the zeros. Furthermore, a function has no zeros/real roots/x-intercepts when the value of the discriminant (b2 - 4ac) is negative.
Try D) a=-2, b=4, c=10 Try B) a=1, b=5, c=12 ∴ Since the discriminant is negative in B), it will not have any real roots.
Polynomial Function Properties
Which of the following polynomials might have 5 turning points, without verifying by graphing?
Solution
The maximum number of turning points in a function equals,
= degree - 1
A function with 5 turning points will have a degree of 6.
This leaves only:
This leaves only:
Properties of Polynomial Functions
Determine which has an even leading coefficient and an odd degree.
Solution
A coefficient is a number in-front of a variable. The degree of a function is the highest exponent on a variable.
Which of the following will have an odd leading coefficient and an odd degree?
Solution
To determine the degree of an equation in factored form, add the exponents of all the common variables that are factored. The leading coefficient is determined by multiplying all the coefficients of the variables in factored form.
Zeros and Turning Points
How many turning points and x-intercepts could the following function have?
Solution
Rule 1:
A polynomial function with degree n, has a maximum of n - 1 turning points.
Rule 2:
The maximum number of x-intercepts (real roots) is equal to the degree, n of the function.
A polynomial function with degree n, has a maximum of n - 1 turning points.
Rule 2:
The maximum number of x-intercepts (real roots) is equal to the degree, n of the function.
Which of the following polynomial functions could not have 3 turning points?
Solution
A polynomial function with degree n, has a maximum of n - 1 turning points.
Functions with degree of 4 or more could have 3 turning points.
The function would have 2 turning points at the most (and a minimum of 0 turning points).
Functions with degree of 4 or more could have 3 turning points.
The function would have 2 turning points at the most (and a minimum of 0 turning points).
Which of the following polynomial functions has an even number of turning points?
Solution
Polynomial functions with even degrees tend to have an odd number of turning points.
Polynomial functions with odd degrees tend to have an even number of turning points.
Polynomial functions with odd degrees tend to have an even number of turning points.
Degree and End Behaviour
Which of the following is the correct end behaviour of the function
Solution
This is just one end behaviour, of the right-hand side. The end behaviour for the left-hand side is as x → -∞, y → +∞.
Which statement is incorrect regarding end behaviours of polynomial functions?
Solution
If the degree is even and the leading coefficient is negative, the ends are in the third and fourth quadrants.
- The even degree means the ends are on the same side of the x-axis
- A negative leading coefficient means the function is reflected vertically
- The even degree means the ends are on the same side of the x-axis
- A negative leading coefficient means the function is reflected vertically
Determine the end behaviours of the function below as x → +∞ and as x → -∞.
Solution
The degree of the function is odd, 5. Therefore the function has end behaviours on opposite sides of the x-axis.
Since the degree is odd and the leading coefficient is negative, the ends are in the second and fourth quadrants.
As x → +∞... y → -∞ (in the fourth quadrant).
As x → -∞... y → +∞ (in the second quadrant).
Since the degree is odd and the leading coefficient is negative, the ends are in the second and fourth quadrants.
As x → +∞... y → -∞ (in the fourth quadrant).
As x → -∞... y → +∞ (in the second quadrant).
Graphing/Sketching Polynomial Functions
Which is true for the function ?
Solution
The function will pass through the x-axis at x = 0 and -4, and will bounce off the x-axis at x = 2.
- You can get the x-intercepts from the funtion.
- At the x-axis, functions 'bounce' when the degree is even, and go through when the degree is odd.
- You can get the x-intercepts from the funtion.
- At the x-axis, functions 'bounce' when the degree is even, and go through when the degree is odd.
To sketch the function the x-intercepts, y-intercept and which other aspect is required?
Solution
With the given information in the question, you are not sure how the function behaves above and below each of the x-intercepts (-1, 0) and (2, 0). You know the function will cross the x-axis at the point (-1, 0) because the binomial has an odd exponent. And you know the function will bounce at (2, 0) because the binomial has an even exponent.
Having either an end behaviour or a point beside an x-intercept will tell you the behaviour of the function at the x-intercept, in other words the direction from which the function will cross or bounce at each x-intercept.
Having either an end behaviour or a point beside an x-intercept will tell you the behaviour of the function at the x-intercept, in other words the direction from which the function will cross or bounce at each x-intercept.
The function has which of the following characteristics?
Solution
The x-intercept occurs where the function equals zero:
From x3... x = 0
From (x - 3)2... x = +3
From (x + 5)... x = -5
The y-intercept occurs where x = 0...
From x3... x = 0
From (x - 3)2... x = +3
From (x + 5)... x = -5
The y-intercept occurs where x = 0...
Sketching Polynomial Functions
In your notebook, sketch a graph of the function
Solution
This gives all the information needed to make a proper sketch. (Exact turning points not required.)
Transformations of Polynomial Functions
State the transformations on the following polynomial.
Solution
Hint
Clear
Info
· Vertical compression by a factor of
· Reflection across the
-axis
· Horizontal compression by a factor of
· Translation
unit(s) right
· Translation unit(s) up
Incorrect Attempts:
CHECK
Hint Unavailable
Factor out the 'k' value first.
Compare to:
The transformations:
Vertical compression by a factor of
Reflection accross the x-axis.
Horizontal compression by a factor of
Translation 1 unit right
Translation 10 units up
Hint
Clear
Info
· Vertical compression by a factor of
· Reflection across the
-axis · Horizontal compression by a factor of
· Translation
unit(s) right · Translation unit(s) up
· Reflection across the
-axis · Horizontal compression by a factor of
· Translation
unit(s) right · Translation unit(s) up
Incorrect Attempts:
CHECK
Hint Unavailable
The transformations:
Vertical compression by a factor of
Reflection accross the x-axis.
Horizontal compression by a factor of
Translation 1 unit right
Translation 10 units up
Factoring Polynomials: The Factor Theorem
(x + 3) is a factor of when ƒ(-3) = 0
Solution
(x + n) is a factor when ƒ(-n) = 0.
How can we verify if x = 2 is an x-intercept of the polynomial:
Solution
The factor theorem says: (x - n) is a factor of ƒ(x) when ƒ(n) = 0.
For the following function (x + 2) is a factor.
Solution
(x + 2) is not a factor when there is a remainder (-10). The factor theorem says: If (x - n) is a factor, then ƒ(n) = 0.
The function has x-intercepts at x = 0, 5.
Solution
-12 = x2(x - 5)
Nope! Expand and then use the factor theorem
Try different substitutions, until eventually f(-2) = 0
Therefore, (x - 2) is a factor.. using polynomial long division (not shown) you should get...
So x = 2... and using the quadratic equation (not shown) for x2 - 3x - 6...
Determine ƒ(5), ƒ(-3) for ƒ(x) = 2x3 - 3x2 - 32x - 15, and factor the equation...
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Using the factor theorem, if (x - n) is a factor, then ƒ(n) = 0.
Therefore (x - 5) is one factor of ƒ(x)
Therefore (x + 3) is one factor of ƒ(x)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The divisor (4x - 7) is a factor of when:
Solution
The factor theorem says: If (x - n) is a factor, then ƒ(n) = 0.
Determine the values of 'a' and 'c' given that (x - 3) and (x + 2) are factors of ƒ(x) = ax3 - x2 - cx - 12 .
Solution
Hint
Clear
Info
a = c =
Incorrect Attempts:
CHECK
Hint Unavailable
The factor theorem says: If (x - n) is a factor, then ƒ(n) = 0...
Solve the system of 2 equations with substitution or elimination... Sub ① in ②...
Hint
Clear
Info
a = c =
Incorrect Attempts:
CHECK
Hint Unavailable
Factoring Polynomials: The Remainder Theorem
The remainder theorem equation, in corresponding form is:
ƒ(x) = d(x)·q(x) + r(x)dividend = (divisor)(quotient) + remainder And in quotient form is:
If the function ƒ(x) has a factor of (x - n), then the remainder can be calculated with ƒ(n)...
Solution
Determine the remainder when is divided by (x - 2).
Solution
remainder =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Substitute the root 2, in ƒ(2) to determine 'R'
(This question could also be solved with factor theorem, which is very similar to the remainder theorem)
remainder =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
A math student has used long division to determine the quotient and remainder of a polynomial. If the remainder is 0, the divisor is (x + 3) and the quotient is , then what dividend was used in the long division?
Solution
Note that when putting the dividend into long division, placeholders with a coefficient of 0 are required. should not be used. Instead use .
Determine the quotient in standard form, if the divisor is (x + 1), the remainder is 4, and the dividend is 3x3 - 2x + 5.
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
When is divided by (x + 1) the remainder is 0. Determine the value of k.
Solution
k =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Given for (x + 1) the remainder is 0... n = -1...
(This question could also be solved with factor theorem, which is very similar to the remainder theorem)
k =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
If (x + 6) is a factor of , find the value of k.
Solution
k =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Given (x + 6) is a factor, the remainder equals zero when n = -6...
(This question could also be solved with factor theorem, which is very similar to the remainder theorem)
k =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
When is divided by (x - 1) and (x + 5) it has the same remainder. Determine the value of n.
Solution
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The Remainder Theorem Part II
Determine the remainder, without the quotient.
Solution
Dividend: ƒ(x) = 3x3 - 2x2 + 10x - 5
Divisor: (x + 4)(x + 3)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The remainder is always linear regardless of the degree of the dividend and divisor... It is either a constant, or has a degree of 1. Unless indicated otherwise, assume the remainder has a degree of 1, and represent as nx + m
From the root (x + 4), determine and substitute ƒ(-4) = -269...
From the root (x + 3), determine and substitute ƒ(-3) = -134...
Now solve the system of equations (using elimination here)...
Determine 'm'..
Therefore the remainder is: 135x + 271
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Given the conditions below, determine the remainder, without the quotient or dividend, when the same divisor is divided into 3·ƒ(x) - 2.
Solution
Dividend: ƒ(x)
Divisor: (x - 1)
Remainder: -2
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The question indicates that the remainder is a constant, so use one variable, 'R' to represent the remainder as a constant.
Substitute...
Now use this value for 3·ƒ(x) - 2...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Factoring Polynomial Functions
The function is equal to which of the following?
Solution
Synthetic Division
Synthetic division works for all divisors.
Solution
Synthetic division only works for divisors that have one possible solution for 'x', for example:
(x + 1), (x - 3), (2x + 3), ...
Not,
(x + 4)(x - 4), (x - 1)(x + 3), 2x2 - 3x + 4
Solve for the remainder using synthetic division, given the divisor: (x + 2)
Solution
ƒ(x) = 2x3 + 5x2 - x - 6
remainder =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The synthetic division,
Quotient: 2x2 + 1x - 3
Remainder: 0
See that this obeys the remainder theorem:
ƒ(x) = d(x)·q(x) + r(x)
dividend = (divisor)(quotient) + remainder
And can be rearranged:
remainder =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Remainder: 0
See that this obeys the remainder theorem: ƒ(x) = d(x)·q(x) + r(x)
dividend = (divisor)(quotient) + remainder And can be rearranged:
Factoring Polynomials (with a Degree of 4 or Lower)
Solve and order by increasing values.
x3 + 6x2 + 3x - 10
Solution
Hint
Clear
Info
x1 = x2 = x3 =
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
x1 = x2 = x3 =
Incorrect Attempts:
CHECK
Hint Unavailable
(x3 - x2 - 9x + 9) ÷ (x2 - 9)
Solution
Hint
Clear
Info
x1 = x2 = x3 =
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
x1 = x2 = x3 =
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
x1 = x2 = x3 =
Incorrect Attempts:
CHECK
Hint Unavailable
x = -1.5, -1, 5
Hint
Clear
Info
x1 = x2 = x3 =
Incorrect Attempts:
CHECK
Hint Unavailable
x = -1.5, -1, 5
3x4 - 28x3 - 32x2 + 112x + 80
Solution
Hint
Clear
Info
x1 = x2 = x3 = x4 =
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
x1 = x2 = x3 = x4 =
Incorrect Attempts:
CHECK
Hint Unavailable
Quotient Form of Polynomial Functions
Which of the following is not equivalent to the others?
Solution
is correct and is called QUOTIENT FORM.
is not equal to the rest.
is not equal to the rest.
Difference of Cubes, Sum of Cubes
Factor, use proper form.
64x3 - 27
Solution
Video
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
125x3 + 216y3
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
Factor by Grouping
Factor the following polynomial by practicing grouping.
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
(-1) and (-6) multiply to +6 and add to -7.
So break (-7x3) apart into: (-x3) and (-6x3)
Of course you can do,
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
So break (-7x3) apart into: (-x3) and (-6x3) Of course you can do,
Terms of Division
Classify the terms for the following.
Solution
12x
3x
4
0
Quotient
Dividend
Remainder
Divisor
The divisor (3x) is what you divide the dividend (12x) by to give you the quotient (4).
There is no remainder, or a remainder of zero.
12x
3x
4
0
Quotient
Dividend
Remainder
Divisor
There is no remainder, or a remainder of zero.
Solving Polynomial Equations
Determine the x-intercepts of , giving exact values.
Solution
Solve , giving exact values.
Solution
Resolving Polynomial Equations
A function passes through the point (1, 30) and has the x-intercepts below. Determine the equation of the function.
Solution
First substitute the x-intercepts, like...
Then substitute the point (1, 30) to determine the value of 'a'...
∴ the equation is:
Polynomial Word Problems
A rectangular prism is nested inside of an outer rectangular prism. The inner volume is The volume of the space between the inner and outer prisms is
If the outer volume is 240 cm3, determine the dimensions of the outer rectangular prism, in a comma-separated list.
Solution
dimensions:
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
First determine an expression for the volume of the outer rectangular prism, in terms of x. Add the space-volume to the inner-volume,
Then determine one factor...
x = 3... Therefore the dimensions are:
(x + 5) = 8
(x + 3) = 6
(2x - 1) = 5
dimensions:
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
(x + 3) = 6
(2x - 1) = 5
Solving Polynomial Inequalities
Multiplying or dividing the variable by a negative requires the inequality sign to be reversed.
Solution
-2x ≥ -4
True,
Solving Polynomial Inequalities
Solve the following inequalities with interval notation. Remember for interval notation:
±∞ ... uses ... ( )>, < ... uses ... ( )
≥, ≤ ... uses ... [ ]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Imagine the roots of a quadratic at x = -3, and x = +3.
The domain exists on either side (-∞ and +∞) of the roots.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The domain exists on either side (-∞ and +∞) of the roots.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Solving Polynomial Inequalities
State the domain using set notation...
x > 4 or x > 8
Solution
x > 4 encompasses x > 8 so use x > 4 in the set notation.
(x + 4)(x - 5) ≤ 0
Solution
Video
The answer will contain the range where ƒ(x) ≤ 0.
The function has roots at x = -4, 5.
The y-value, ƒ(x) is negative in the interval: {xεR | -4 ≤ x ≤ 5}
The function has roots at x = -4, 5.
The y-value, ƒ(x) is negative in the interval: {xεR | -4 ≤ x ≤ 5}
x(x - 1) + (x - 1) ≤ 0
Solution
Simplify the function:
The answer will contain the range where ƒ(x) ≤ 0.
The function has roots at x = -1, 1.
The y-value, ƒ(x) is negative in the interval: {xεR | -1 ≤ x ≤ 1}
The function has roots at x = -1, 1.
The y-value, ƒ(x) is negative in the interval: {xεR | -1 ≤ x ≤ 1}
x(x + 4)(x + 4) ≥ 0
Solution
The domain corresponds to the regions where y is positive (because of ≥ 0).
The end behaviours are in quadrant 1 and 3.
The function is tangent to the x-axis at x = -4.
The end behaviours are in quadrant 1 and 3.
The function is tangent to the x-axis at x = -4.
x4 - 10x2 + 9 > 0
Solution
Factor fully.
The roots occur at -3, -1, 1, 3.
Determine where the function is positive (Given from the interval " > 0").
The function has a degree of 4 (even) and a positive leading coefficient, therefore it has end behaviours in quadrant 1 and 2.
The function is positive on the interval: {xεR | x < -3, -1 < x < 1, x > 3}
Determine where the function is positive (Given from the interval " > 0").
The function has a degree of 4 (even) and a positive leading coefficient, therefore it has end behaviours in quadrant 1 and 2.
The function is positive on the interval: {xεR | x < -3, -1 < x < 1, x > 3}
Rational Functions
Exponents Review
Express each as a power with a base of 3
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
Root Equation Review
Solve for the variable:
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
x1 = x2 =
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
x1 = x2 =
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
x1 = x2 =
Incorrect Attempts:
CHECK
Hint Unavailable
Make sure to move first
Hint
Clear
Info
x1 = x2 =
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Video
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Video
Hint
Clear
Info
x1 = ━━x2 =
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
x1 = ━━x2 =
Incorrect Attempts:
CHECK
Hint Unavailable
Practice With Rational Equation Algebra
Solve (and state your answers in increasing order).
Solution
Hint
Clear
Info
x1 = x2 =
Incorrect Attempts:
CHECK
Hint Unavailable
Cross multiply first to 'get rid of the fractions'..
Hint
Clear
Info
x1 = x2 =
Incorrect Attempts:
CHECK
Hint Unavailable
Rational Equation Word Problems - Working Together
Solve the rational equation word problems, and remember the general form equation for problems on 'working together'.
Marcello takes 9 more minutes than Koji to make 10 pizzas. Working together, they can make 10 pizzas in 20 minutes. How long does it take Koji to make 10 pizzas when he works alone?
Solution
t =
Hint
Clear
Info
Incorrect Attempts:
CHECK
minutes
Hint Unavailable
Let 'x' be the time for Koji to make 10 pizzas.
Let 'x + 9' be the time for Marcello to make 10 pizzas.
Koji takes 36 minutes...
t =
Hint
Clear
Info
Incorrect Attempts:
CHECK
minutes
Hint Unavailable
Let 'x + 9' be the time for Marcello to make 10 pizzas. Koji takes 36 minutes...
Sandi and John are computer programmers with different experience levels. It takes John 10 hours less than double the time it takes Sandi to write 2000 lines of code. Working together, it takes them 12 hours. How long does it take Sandi working alone?
Solution
t =
Hint
Clear
Info
Incorrect Attempts:
CHECK
hours
Hint Unavailable
Let 'x' be the time for Sandi to write 2000 lines of code.
Let '2x - 10' be the time for John to write 2000 lines of code.
Takes Sandi 20 hours.. [Can't take Sandi 3 hours because then for John, 2(3) - 10 would be negative time]
t =
Hint
Clear
Info
Incorrect Attempts:
CHECK
hours
Hint Unavailable
Let '2x - 10' be the time for John to write 2000 lines of code. Takes Sandi 20 hours.. [Can't take Sandi 3 hours because then for John, 2(3) - 10 would be negative time]
Recognizing Rational Functions
Which of the following is a rational function?
Solution
Rational functions must have polynomial functions in the numerator (dividend) and denominator (divisor). In other words, the quotient must be written with polynomials.
Polynomials cannot have square roots on the independent variable (but a rational function can have square root coefficients).
Polynomials cannot have square roots on the independent variable (but a rational function can have square root coefficients).
Rational Functions: Factoring, X-intercept(s), and Y-intercept
Determine the 'x' and 'y' intercepts in coordinate form (x, y). Round your answers to one decimal place and list in increasing order, where applicable.
1) x-intercept(s): solve for the numerator2) y-intercept: set x = 0 and solve for 'y'
Solution
Hint
Clear
Info
x-intercepts:
y-intercept:
Incorrect Attempts:
CHECK
Hint Unavailable
Factor fully,
x-intercepts: (0, 0), (0.5, 0), (2, 0).
Solve for y-intercept with ƒ(0), if any...
y-intercept: (0, 0)
Hint
Clear
Info
x-intercepts:
y-intercept:
y-intercept:
Incorrect Attempts:
CHECK
Hint Unavailable
Solve for y-intercept with ƒ(0), if any... y-intercept: (0, 0)
Solution
Hint
Clear
Info
x-intercepts:
y-intercept:
Incorrect Attempts:
CHECK
Hint Unavailable
Simplify & factor fully,
Using the quadratic equation to determine the x-intercepts...
x-intercepts: (-1.8, 0), (3.8, 0)
Solve for y-intercept with ƒ(0), if any...
y-intercept: (0, 1.2)
Hint
Clear
Info
x-intercepts:
y-intercept:
y-intercept:
Incorrect Attempts:
CHECK
Hint Unavailable
Solve for y-intercept with ƒ(0), if any... y-intercept: (0, 1.2)
Rational Expressions: Restrictions
Simplify and state the restrictions. (Enter your answers in increasing order, and where applicable leave as fully reduced fraction, instead of repeating decimals)
Solution
Hint
Clear
Info
x ≠ ━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
x ≠ ━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
a ≠ ━━ ,
b ≠ ━━ , ━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
a ≠ ━━ ,
b ≠ ━━ , ━━
b ≠ ━━ , ━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Video
Hint
Clear
Info
x ≠ ,
,
,
━━ ,
Incorrect Attempts:
CHECK
Hint Unavailable
Enter in increasing order:
(Don't forget to state a restriction on anything that was ever a denominator, so even though the 7x-1 gets flipped to the top, it still has to be included in the restriction list!)
Hint
Clear
Info
x ≠ ,
,
,
━━ ,
Incorrect Attempts:
CHECK
Hint Unavailable
Enter in increasing order:
(Don't forget to state a restriction on anything that was ever a denominator, so even though the 7x-1 gets flipped to the top, it still has to be included in the restriction list!)
Solution
Hint
Clear
Info
x ≠ ,
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
x ≠ ,
Incorrect Attempts:
CHECK
Hint Unavailable
Horizontal and Vertical Asymptotes: Degree of Numerator < Degree of Denominator
Determine the horizontal and vertical asymptotes of the following functions. (Order from low to high, where applicable)
The horizontal asymptote (HA) is always y = 0 + 'd' when the degree of the numerator is less than the degree of the denominator. (where 'd' is the vertical translation, not shown here)
Solution
Hint
Clear
Info
x1 = x2 =
y =
Incorrect Attempts:
CHECK
Hint Unavailable
Vertical asymptote(s) @ x = -3, 2
Horizontal asymptote(s) @ y = 0
Hint
Clear
Info
x1 = x2 =
y =
y =
Incorrect Attempts:
CHECK
Hint Unavailable
Horizontal asymptote(s) @ y = 0
Solution
Hint
Clear
Info
x1 = x2 =
y =
Incorrect Attempts:
CHECK
Hint Unavailable
Vertical asymptote(s) @ x = -2, 2
Horizontal asymptote(s) @ y = 0
Hint
Clear
Info
x1 = x2 =
y =
y =
Incorrect Attempts:
CHECK
Hint Unavailable
Horizontal asymptote(s) @ y = 0
Solution
Hint
Clear
Info
x1 = x2 =
y =
Incorrect Attempts:
CHECK
Hint Unavailable
Vertical asymptote(s) @ x = -0.5, 6
Horizontal asymptote(s) @ y = 0
Hint
Clear
Info
x1 = x2 =
y =
y =
Incorrect Attempts:
CHECK
Hint Unavailable
Horizontal asymptote(s) @ y = 0
Horizontal and Vertical Asymptotes: Degree of Numerator = Degree of Denominator
Determine the horizontal and vertical asymptotes of the following functions.
The horizontal asymptote (HA) is always when the degree of the numerator is equal to the degree of the denominator (where 'd' is the vertical translation, not shown here)
Solution
Hint
Clear
Info
Vertical asymptote(s) @ x = ━━
Horizontal asymptote(s) @ y =
Incorrect Attempts:
CHECK
Hint Unavailable
Vertical asymptote(s) @ x = -2/3
Horizontal asymptote(s) @ y = 12/3 = 4
Hint
Clear
Info
Vertical asymptote(s) @ x = ━━
Horizontal asymptote(s) @ y =
Horizontal asymptote(s) @ y =
Incorrect Attempts:
CHECK
Hint Unavailable
Horizontal asymptote(s) @ y = 12/3 = 4
Solution
Hint
Clear
Info
Vertical asymptote(s): x =
,
Horizontal asymptote(s): y =
Incorrect Attempts:
CHECK
Hint Unavailable
Vertical asymptote(s) @ x = -2, 1
Horizontal asymptote(s) @ y = -5/2 = -2.5
Hint
Clear
Info
Vertical asymptote(s): x =
,
Horizontal asymptote(s): y =
Horizontal asymptote(s): y =
Incorrect Attempts:
CHECK
Hint Unavailable
Horizontal asymptote(s) @ y = -5/2 = -2.5
Solution
Hint
Clear
Info
Vertical asymptote(s): x =
,
,
Horizontal asymptote(s): y = ━━
Incorrect Attempts:
CHECK
Hint Unavailable
Vertical asymptote(s) @ x = -3/2, 3/2, -1
(order as: x = -1.5, -1, 1.5)
Horizontal asymptote(s) @ y = -7/4
Hint
Clear
Info
Vertical asymptote(s): x =
,
,
Horizontal asymptote(s): y = ━━
Horizontal asymptote(s): y = ━━
Incorrect Attempts:
CHECK
Hint Unavailable
(order as: x = -1.5, -1, 1.5)
Horizontal asymptote(s) @ y = -7/4
Solution
Hint
Clear
Info
Vertical asymptote(s): x =
Horizontal asymptote(s): y =
Incorrect Attempts:
CHECK
Hint Unavailable
Vertical asymptote(s) @ x = -1 only.
! Careful. There is no vertical asymptote at x = +1 because it cancels out on the top and the bottom. This is a hole!
Horizontal asymptote(s) @ y = 2
Hint
Clear
Info
Vertical asymptote(s): x =
Horizontal asymptote(s): y =
Horizontal asymptote(s): y =
Incorrect Attempts:
CHECK
Hint Unavailable
! Careful. There is no vertical asymptote at x = +1 because it cancels out on the top and the bottom. This is a hole!
Horizontal asymptote(s) @ y = 2
Solution
Hint
Clear
Info
Vertical asymptote(s) @ x = ━━ , ━━
Horizontal asymptote(s) @ y =
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Vertical asymptote(s) @ x = ━━ , ━━
Horizontal asymptote(s) @ y =
Horizontal asymptote(s) @ y =
Incorrect Attempts:
CHECK
Hint Unavailable
Horizontal and Vertical Asymptotes: Degree of Numerator > Degree of Denominator... (numerator = denominator + 1)
Determine the oblique (slant) and vertical asymptotes of the following functions.
There is no horizontal asymptote (HA) when the degree of the numerator is one more than the degree of the denominator.The slant/oblique asymptote is the quotient of
Solution
Hint
Clear
Info
Vertical asymptote(s): x =
Oblique asymptote(s): y =
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Vertical asymptote(s): x =
Oblique asymptote(s): y =
Oblique asymptote(s): y =
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Vertical asymptote(s) @ x = ━━
Oblique asymptote(s) @ y =
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Vertical asymptote(s) @ x = ━━
Oblique asymptote(s) @ y =
Oblique asymptote(s) @ y =
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Vertical asymptote(s) @ x = ━━ ,
Oblique asymptote(s) @ y = ━━ x -
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Vertical asymptote(s) @ x = ━━ ,
Oblique asymptote(s) @ y = ━━ x -
Oblique asymptote(s) @ y = ━━ x -
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Vertical asymptote(s) @ x =
,
Oblique asymptote(s) @ y =
Incorrect Attempts:
CHECK
Hint Unavailable
Vertical asymptote: x = -3, 3
Horizontal asymptote: none
Oblique (slant) asymptote: y = x + 2
Hint
Clear
Info
Vertical asymptote(s) @ x =
,
Oblique asymptote(s) @ y =
Oblique asymptote(s) @ y =
Incorrect Attempts:
CHECK
Hint Unavailable
Horizontal asymptote: none
Oblique (slant) asymptote: y = x + 2
Rational Functions: Holes
Determine where holes exist for the following functions.
Holes exist for all values where the numerator cancels with the denominator...
Solution
Hole @ x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hole @ x = 3
Hole @ x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hole @ x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hole @ x = -4
Hole @ x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hole @ x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hole @ x = 0
Hole @ x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Simplifying Rational Functions
For the following function, which of the following statements is true?
Solution
Simplify,
A hole occurs when the same binomial is in the numerator and denominator, in this case: (3x + 2).
Though the (3x + 2) cancels in the denominator, there is still a restriction at x = -2/3.
You might think that there is a vertical asymptote at -⅔, or that a slant (oblique) asymptote exists at y = 2x - 2, but holes win every time !
The graph just looks like a linear function of y = 2x - 2, with a hole at x = -.
Though the (3x + 2) cancels in the denominator, there is still a restriction at x = -2/3.
You might think that there is a vertical asymptote at -⅔, or that a slant (oblique) asymptote exists at y = 2x - 2, but holes win every time !
The graph just looks like a linear function of y = 2x - 2, with a hole at x = -.
Positive and Negative Intervals
Given the graph of the function
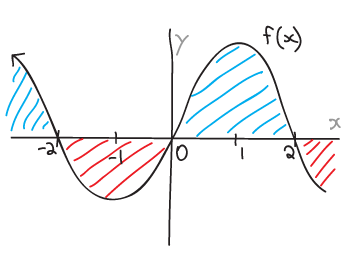
Determine the positive and negative intervals for the diagram of the function above.
Solution
Positive and negative intervals occur are based on where the function exists above or below the x-axis for positive or negative values of y.
Determine the intervals of increase and decrease for the diagram of the function above.
Solution
Think of the slope of the tangent at any one point. The intervals of increase have a tangent with a positive slope, and the intervals of decrease have a tangent with a negative slope.
Graphs of Rational Functions: Domain, Range, Increase-Decrease Intervals, and Positive-Negative Intervals
Determine the positive and negative intervals of the following function, using set notation.
Solution
Hint
Clear
Info
Positive: { XER | }
Negative: { XER | }
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Positive: { XER | }
Negative: { XER | }
Negative: { XER | }
Incorrect Attempts:
CHECK
Hint Unavailable
Reciprocal Coordinate
A point P(4, 21) exists for the following function . Determine the corresponding coordinate of the reciprocal of this function.
Solution
The x-value is the same, while the reciprocal of the y-value is
Reciprocal of Absolute Value Function
The reciprocal of the absolute value function y = ¼|x| - 2 has vertical asymptote(s) at
Solution
Graphing the Reciprocals of Linear Functions
For the reciprocal of the function , determine:
The vertical and horizontal asymptotes, and the domain and range.
Solution
Video
Hint
Clear
Info
Domain:{ XER | x ≠ ━━}
Range: { YER | y ≠ }
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Domain:{ XER | x ≠ ━━}
Range: { YER | y ≠ }
Range: { YER | y ≠ }
Incorrect Attempts:
CHECK
Hint Unavailable
The positive/negative intervals.
Solution
Hint
Clear
Info
Positive:{ XER | ━━}
Negative:{ YER | ━━}
Incorrect Attempts:
CHECK
Hint Unavailable
To find positive/negative intervals substitute x-values on either sides of the vertical asymptotes into ƒ(x), and check if function is positive or negative...
Since the vertical asymptote is x = 5/4, check the intervals: x<5/4, and x>5/4...
For x < 5/4...
The function is negative: {XER | x < 5/4}
For x > 5/4...
The function is positive: {XER | x > 5/4}
Hint
Clear
Info
Positive:{ XER | ━━}
Negative:{ YER | ━━}
Negative:{ YER | ━━}
Incorrect Attempts:
CHECK
Hint Unavailable
Since the vertical asymptote is x = 5/4, check the intervals: x<5/4, and x>5/4...
For x < 5/4... The function is negative: {XER | x < 5/4}
For x > 5/4... The function is positive: {XER | x > 5/4}
The increasing/decreasing intervals.
Solution
Hint
Clear
Info
Decreasing:{ XER | x ≠ ━━}
Incorrect Attempts:
CHECK
Hint Unavailable
Make a sketch to visualize the increasing/decreasing intervals, using...
- HA: y = 0
- VA: x =
- As x → -∞, y → 0
- As x → +∞, y → 0
From this you can see...
- Increasing: none
- Decreasing: {XER / x ≠ }, or (−∞, ) ∪ (, ∞)
Hint
Clear
Info
Decreasing:{ XER | x ≠ ━━}
Incorrect Attempts:
CHECK
Hint Unavailable
- HA: y = 0
- VA: x =
- As x → -∞, y → 0
- As x → +∞, y → 0
- Increasing: none
- Decreasing: {XER / x ≠ }, or (−∞, ) ∪ (, ∞)
Graphing the Reciprocals of Quadratic Functions
For the reciprocal of the function , determine:
The vertical and horizontal asymptotes, and the domain and range.
Solution
Hint
Clear
Info
Domain:{ XER | x ≠ , ━━}
Range: { YER | y ≠ }
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Domain:{ XER | x ≠ , ━━}
Range: { YER | y ≠ }
Range: { YER | y ≠ }
Incorrect Attempts:
CHECK
Hint Unavailable
Determine where a point of inflection (turning point) exists.
Solution
The turning point exists between the vertical asymptotes, -4 and -3/2...
The positive/negative intervals.
Solution
Hint
Clear
Info
Positive:{ XER | ━━}
Negative:{ XER | ━━}
Incorrect Attempts:
CHECK
Hint Unavailable
Make an interval chart using the asymptotes: -4 and -3/2
(-∞, -4) (-4, -3/2) (-3/2, ∞)
(2x + 3) — — +
(x + 4) — + +
Result: + — +
Positive: { -4 > x > }, or (-∞, -4) ∪ (, ∞)
Negative: { -4 < x < }, or (-4, )
Hint
Clear
Info
Positive:{ XER | ━━}
Negative:{ XER | ━━}
Negative:{ XER | ━━}
Incorrect Attempts:
CHECK
Hint Unavailable
| (-∞, -4) | (-4, -3/2) | (-3/2, ∞) | |
| (2x + 3) | — | — | + |
| (x + 4) | — | + | + |
| Result: | + | — | + |
Negative: { -4 < x < }, or (-4, )
The increasing/decreasing intervals, using interval notation: ( ) [ ].
Solution
Hint
Clear
Info
Increasing:
(
-∞ ,
)
∪
(
, ━━
)
Decreasing:
(
━━ , ━━
)
∪
(
━━ , ∞
)
Incorrect Attempts:
CHECK
Hint Unavailable
Make a sketch to visualize the increasing/decreasing intervals, using...
- HA: y = 0
- VA: x = -4,
- As x → -∞, y → 0
- As x → +∞, y → 0
Determine the axis of symmetry of the local maximum, either from the vertex of the original function or from the midpoint of the vertical asymptotes.
After a sketch, you can see...
- Increasing: {XER / x < -4, -4 < x < }, or (-∞, -4) ∪ (-4, )
- Decreasing: {XER / < x < , x > }, or (, ) ∪ (, ∞)
Hint
Clear
Info
Increasing:
(
-∞ ,
)
∪
(
, ━━
)
Decreasing: ( ━━ , ━━ ) ∪ ( ━━ , ∞ )
Decreasing: ( ━━ , ━━ ) ∪ ( ━━ , ∞ )
Incorrect Attempts:
CHECK
Hint Unavailable
- HA: y = 0
- VA: x = -4,
- As x → -∞, y → 0
- As x → +∞, y → 0
- Increasing: {XER / x < -4, -4 < x < }, or (-∞, -4) ∪ (-4, )
- Decreasing: {XER / < x < , x > }, or (, ) ∪ (, ∞)
Graphing the Reciprocals of Quadratic Functions
For the reciprocal of the function , determine:
The vertical and horizontal asymptotes, and the domain and range. Solution
The x-intercepts, positive/negative intervals, and increasing/decreasing intervals. Solution
Determine the end behaviour of the function.
Solution
From the previous sketch, see that: x → -∞, y → 0, x → +∞, y → 0
Reciprocals of Quadratic Functions: The Relationship of Roots and Vertical Asymptotes
For the reciprocal of the following functions, determine if any vertical asymptotes exist.
Solution
Solution
Reciprocal Function Equations
Determine an equation of a reciprocal function given the following information.
Real root at (-1, 0) and a hole at x = 1
Solution
Hole at x = 3, horizontal asymptote at y = 0, and vertical asymptote at x = -5.
Solution
A vertical asymptote exists at x = 10, and a x-intercept of x = 5, given the following function: Solution
Describing Graphs of Rational Functions
Where applicable, determine the increasing, decreasing, positive, and negative intervals.
Solution
Common factor,
Determine the features:
- VA: x =
- HA: y = -2 (when degree of numerator & denominator are equal: use ratio of leading coefficients)
- y-intercept: y =
- x-intercept: x =
Make a table to determine the positive/negative intervals (note: 0 is not positive or negative)
(-∞, ) (, ) (, ∞)
(2 - 3x) + + -
(2x - 1) - + +
Results: - + -
- Positive: {XER / < x < }, or (, ]
- Negative: {XER / > x > }, or (-∞, ) ∪ [, ∞)
Make a quick sketch in your notes (not shown) to determine the intervals of increase and decrease
- Increase: none
- Decrease: {XER / x ≠}, or (-∞, ) ∪ (, ∞)
- VA: x =
- HA: y = -2 (when degree of numerator & denominator are equal: use ratio of leading coefficients)
- y-intercept: y =
- x-intercept: x =
| (-∞, ) | (, ) | (, ∞) | |
| (2 - 3x) | + | + | - |
| (2x - 1) | - | + | + |
| Results: | - | + | - |
- Positive: {XER / < x < }, or (, ]
- Negative: {XER / > x > }, or (-∞, ) ∪ [, ∞)
- Increase: none
- Decrease: {XER / x ≠}, or (-∞, ) ∪ (, ∞)
Reciprocal Function Word Problem: Substitution
The concentration of an anti-nausea remedy in the body can be determined with the following function where ƒ(t) is concentration in mg/L, and t is time in hours. Determine the time from initial dosage, when the concentration in the body is 1.40 gm/L.
Solution
t =
Hint
Clear
Info
Incorrect Attempts:
CHECK
hours
Hint Unavailable
Solve using the quadratic formula, where a = 2.8, b = -23.6, and c = -16.8
t = -0.66, 9.09 hours. [time cannot be negative]
t =
Hint
Clear
Info
Incorrect Attempts:
CHECK
hours
Hint Unavailable
t = -0.66, 9.09 hours. [time cannot be negative]
Linear & Quadratic Inequalities Practice
Solve
Solution
Solution
Solution
or
or
Solution
Solution
Solution
Rational Inequalities
Solve algebraically.
Solution
Move the terms to the same side, simplify, and factor,
To find where the function ƒ(x) is negative (< 0)... Don't worry about the binomial that results in the imaginary number (2x2 + 1). Set up an interval chart with ranges between any of the roots and vertical asymptotes (if any),
(-∞, ) (, ) (, ∞)
(2x + 1) — + +
(2x - 1) — — +
result: (—)(—) = + (+)(—) = — (+)(+) = +
The rational function is negative in the regions,
| (-∞, ) | (, ) | (, ∞) | |
| (2x + 1) | — | + | + |
| (2x - 1) | — | — | + |
| result: | (—)(—) = + | (+)(—) = — | (+)(+) = + |
Solution
Move the terms to the same side, simplify, and factor,
To find where the function ƒ(x) is negative (< 0)... Set up an interval chart with the ranges between any of the roots (x = -2) and vertical asymptotes (x = -3, +3)
(-∞, -3) (-3, -2) (-2, 3) (3, ∞)
(2 + x) — — + +
(3 + x) — + + +
(3 - x) + + + —
result: + — + —
The rational function is negative in the regions,
| (-∞, -3) | (-3, -2) | (-2, 3) | (3, ∞) | |
| (2 + x) | — | — | + | + |
| (3 + x) | — | + | + | + |
| (3 - x) | + | + | + | — |
| result: | + | — | + | — |
Trigonometric Functions
Principal and Acute Angle
Convert the missing angles. Solution
| Principal Angle | Acute Angle |
| 80˚ | 80˚ |
| -290˚ | 70˚ |
| 240˚ | (I) |
| -200˚ | (II) |
Converting Degrees and Radians
Convert the following angle to radian units:
Solution
60˚
Multiply by ..
Converting Degrees and Radians
Convert the following angle to degree units:
Solution
∠ =
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Multiply by ...
∠ =
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Converting Degrees and Radians
Convert 4.30 radians into degrees.
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Radian Definition
Determine the arc length of a circle created by a 4.5 radian angle if the radius of the circle is 10cm.
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
Trig and Operations with Fractions Refresher
Simplify fully.
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Reciprocal Trig Ratios
Determine the value of the reciprocal trig ratio,
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Explain the difference between a reciprocal and an inverse of the following...
Solution
The reciprocal divides '1' by the 'y'-values of the function. For instance [not shown], asymptotes are formed where the function had y = 0...
The inverse represents the angle,
Exact Values of Trig Ratios: Something to Watch
The exact value of cos is
Solution
Video
Although this seems correct, the answer cannot have a square root in the denominator!
To derationalize the denominator, multiply the top and bottom by the square root:
To derationalize the denominator, multiply the top and bottom by the square root:
Exact Values of Trig Ratios
The exact value of cos
Solution
Video
Use the unit circle...
Principle angle = 240˚...
In quadrant 3, cos is negative...
Related acute angle = 60˚...
Using special triangles...
cos of 60˚...
= -1/2
Principle angle = 240˚...
In quadrant 3, cos is negative...
Related acute angle = 60˚...
Using special triangles...
cos of 60˚...
= -1/2
Exact Values of Trig Ratios
Calculate the exact value of sin
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Corresponds to the special triangle angle of 60˚. Use special triangles to find sin(60˚).
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Exact Values of Trig Ratios
Determine the exact value of tan
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Special Angles in Standard Position
Determine the related acute angle given that cscθ = -2 and cosθ > 0, find θ.
Solution
Video
cscθ = -2 so sinθ = -1/2
sin is negative in quadrants III and IV.
cos is positive (cosθ > 0) in quadrants I and IV.
So the both conditions (cscθ = -2 and cosθ > 0) must occur in quadrant IV.
Drawing the special triangle and determining the related acute angle gives 30˚ or pi/6.
sin is negative in quadrants III and IV.
cos is positive (cosθ > 0) in quadrants I and IV.
So the both conditions (cscθ = -2 and cosθ > 0) must occur in quadrant IV.
Drawing the special triangle and determining the related acute angle gives 30˚ or pi/6.
Special Acute Reflex Angles in the CAST System
Given that , determine , , , , and for
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Characteristics of Graphs of Trig Parent Functions
Which of the following is not a similarity between the functions ƒ(x) = sinθ and ƒ(x) = cosθ?
Solution
Furthermore the following features are also similar: amplitude, range.
The only differences are the x-intercepts and y-intercepts.
The only differences are the x-intercepts and y-intercepts.
Characteristics of Graphs of Trig Parent Functions
How many times do the functions ƒ(x) = sinθ and ƒ(x) = cosθ cross the x-axis in the domain -360˚ ≤ θ ≤ 360˚, respectively?
Solution
Hint
Clear
Info
&
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
&
Incorrect Attempts:
CHECK
Hint Unavailable
How many times do the functions ƒ(x) = sinθ and ƒ(x) = cosθ cross 'eachother' in the domain -360˚ ≤ θ ≤ 360˚?
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Characteristics of Graphs of Trig Parent Functions
The period of ƒ(x) = sinθ over the domain -360˚ ≤ θ ≤ 360˚ is not 720˚, rather it is 360˚ or 2π radians.
Solution
The period is not determined by the domain. Rather, the period is always the measurement of the x-axis over just one cycle.
Characteristics of Graphs of Trig Parent Functions
The domain range, and period of the three main trig functions are given below. Fill in the blanks. Solution
| sin(θ) | cos(θ) | tan(θ) | |
| Domain | x∈ℝ | x∈ℝ | x ≠ + n·π, n∈I, n = {...-1, 0, 1, ...} |
| Range | y∈ℝ, -1 ≤ y ≤ 1 | __________ | y∈ℝ |
| Period | 2π | 2π | π |
Hint
Clear
Info
y∈ℝ, ≤ y ≤
Incorrect Attempts:
CHECK
Hint Unavailable
Make a quick sketch of cos(θ)... see that the maximum is +1 and the minimum is -1, so the range is: y∈ℝ, -1 ≤ y ≤ 1
State the x-intercepts in periodic notation in terms of pi, for the function f(x) = sin(θ).
Solution
Remember, or make a quick sketch, and see that some of the x-intercepts are: 0, π, 2π, so the x-intercepts are..
π·n, n∈I
(n∈I means 'n' is all real integers)
Trig Parent Functions
The amplitude of y = tan(θ) is:
Solution
The graph of tan(θ) has vertical asymptotes... therefore the amplitude is infinity, or undefined...
Reciprocal Trig Functions
Which of the following is not a reciprocal of the function, ƒ(x) = cosθ?
Solution
The inverse of cos, cos-1(θ) is not the same as reciprocal! Just think of reciprocal as flipping, with 1 over it...
Order of Transformations of Trig Functions
Determine the recommended order to apply the transformations according to order of operations. Sort by dragging, starting with the first operation at the top.
Solution
Video
y = a · sin (k(x - c)) + d
Vertical Stretch/Compression (a)
Phase Shift (c)
Horizontal Stretch/Compression (k)
Vertical Shift (d)
- Horizontal Stretch/Compression (k)
- Phase Shift (c)
- Vertical Stretch/Compression (a)
- Vertical Shift (d)
Vertical Stretch/Compression (a)
Phase Shift (c)
Horizontal Stretch/Compression (k)
Vertical Shift (d)
- Horizontal Stretch/Compression (k)
- Phase Shift (c)
- Vertical Stretch/Compression (a)
- Vertical Shift (d)
Transformations of Trig Functions
State the horizontal transformation of
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
k = ...
Horizontal stretch by a factor of ...
Horizontal stretch by a factor of 3
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Horizontal stretch by a factor of ... Horizontal stretch by a factor of 3
Transformations of Trig Functions
Transform the points (0, 2) (1, 1) and (2, 0) with a horizontal stretch by a factor of 2 (k = 0.5) and state their images.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Transformations of Trig Functions
The function, is translated right.
Solution
True. The function, is translated right.
Transformations of Trig Functions: Phase Shift
Determine the horizontal translation (phase shift) in the function
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Translated right.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Transformations of Trig Functions
The domain of the function, is x∈ℝ.
Solution
The domain of all sin and cos functions is x∈ℝ... It's the range that depends on the transformations...
Transformations of Trig Functions: Domain and Range
Determine the domain and range for the following trigonometric functions.
Solution
Video
Transformations of Trig Functions
The following functions have the same domain, range, x-intercepts, and y-intercepts, but don't overlap.
Solution
Transformations of Trig Functions
Determine the range of the function,
Solution
Hint
Clear
Info
y∈ℝ, ≤ y ≤
Incorrect Attempts:
CHECK
Hint Unavailable
The amplitude is 2, and the axis of symmetry is shifted down to y = -2.
So the maximum is y = 0, and the minimum is y = -4.
Hint
Clear
Info
y∈ℝ, ≤ y ≤
Incorrect Attempts:
CHECK
Hint Unavailable
So the maximum is y = 0, and the minimum is y = -4.
Transformations of Trig Functions
Determine which of the following is equivalent to the function, .
Solution
Solve by graphing the transformations to check overlapping functions, or solve by plugging in points in radians and comparing the outputs, which is faster. Plug in and if the functions are equivalent, the outputs will be the same.
Therefore the functions and are equivalent.
Transformations of Trig Functions
Which of the following set of transformations would transform the graph of ƒ(x) = cos(x) into the function below.
Solution
g(x) = 2cos(3x - ) + 1
Vertical stretch by a factor of 2, horizontally compressed , translated right, and translated 1 unit up.
Transformations of Trig Functions
Given the function,
Determine all the transformations from the parent cosine function.
Solution
Hint
Clear
Info
· Reflection in the axis
· Vertical compression by a factor of ──
· And a horizontal compression by a factor of ──
· Translated units
· Translated units
Incorrect Attempts:
CHECK
Hint Unavailable
· Reflection in the x-axis
· Vertical compression by a factor of
· Horizontal compression by a factor of
· Translated units right
· Translated 2 units down
Hint
Clear
Info
· Reflection in the axis
· Vertical compression by a factor of ──
· And a horizontal compression by a factor of ──
· Translated units
· Translated units
· Vertical compression by a factor of ──
· And a horizontal compression by a factor of ──
· Translated units
· Translated units
Incorrect Attempts:
CHECK
Hint Unavailable
· Vertical compression by a factor of
· Horizontal compression by a factor of
· Translated units right
· Translated 2 units down
Determine the value of ƒ(x) when x = , and reduce fully.
Solution
Hint
Clear
Info
ƒ(x) = ───
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
ƒ(x) = ───
Incorrect Attempts:
CHECK
Hint Unavailable
Period of Trig Functions
Given the period of a trig function equals 20, determine the exact value of k, in radians.
Solution
y = a · sin [k(x - c)] + d
ƒ(x) =
Hint
Clear
Info
Incorrect Attempts:
CHECK
radians
Hint Unavailable
For the period, (T = 20)
ƒ(x) =
Hint
Clear
Info
Incorrect Attempts:
CHECK
radians
Hint Unavailable
Transformations of Trig Functions
The period of the function, ƒ(x) = -5cos(-4x + 2), in radians is:
Solution
period =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
ƒ(x) = a•sin[k(x - d)] + c
k = -4
period =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
k = -4
Solving for the Independent Variable in the argument of a Trig Function
Given the function below...
Solve for x algebraically, in radians, rounded to the nearest hundredth decimal place.
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
rad
Hint Unavailable
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
rad
Hint Unavailable
Determine the next value of 'x', rounded to the nearest hundredth decimal place, where the function equals 5, over the interval: 0 ≤ x ≤ 0.5π
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Using the cast system, sin is positive (1/2), at π/6 and 5π/6... So
And,
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Features of Trig Functions
Determine the features of the function below. Reduce your answers fully.
The amplitude
Solution
a =
Hint
Clear
Info
Incorrect Attempts:
CHECK
ƒ(x) = a·sin[k(x - d)] + c
ƒ(x) = a·sin[k(x - d)] + c
a = 75
a =
Hint
Clear
Info
Incorrect Attempts:
CHECK
ƒ(x) = a·sin[k(x - d)] + c
a = 75
The vertical translation
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
units up
Hint Unavailable
ƒ(x) = a·sin[k(x - d)] + c
10 units up
Hint
Clear
Info
Incorrect Attempts:
CHECK
units up
Hint Unavailable
10 units up
The equation of the axis of symmetry.
Solution
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
ƒ(x) = a·sin[k(x - d)] + c
y = 10
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
y = 10
The period
Solution
period =
Hint
Clear
Info
–––––
Incorrect Attempts:
CHECK
Hint Unavailable
ƒ(x) = a·sin[k(x - d)] + c
k =
period =
Hint
Clear
Info
–––––
Incorrect Attempts:
CHECK
Hint Unavailable
k =
The horizontal translation
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
units right
Hint Unavailable
units right.
Hint
Clear
Info
Incorrect Attempts:
CHECK
units right
Hint Unavailable
The y-intercept.
Solution
Hint
Clear
Info
( , )
Incorrect Attempts:
CHECK
Hint Unavailable
The y-intercept when t = 0
The point is (0, 31)
Hint
Clear
Info
( , )
Incorrect Attempts:
CHECK
Hint Unavailable
The maximum y-value.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The maximum value occurs at a + c
ƒ(x) = a•sin[k(x - d)] + c
y = 85
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
ƒ(x) = a•sin[k(x - d)] + c
y = 85
Word Problems with Trig Functions: Ferris Wheel
A large ferris wheel at a circus has a diameter of 50m with a platform to mount it at the lowest point 2m above ground level. One full ride around the wheel takes 4 minutes. Find the following
 |
The amplitude
Solution
a =
Hint
Clear
Info
Incorrect Attempts:
CHECK
meters
Hint Unavailable
A point on the wheel oscillates between a maximum height of 52m, and a minimum height of 2m.
a =
Hint
Clear
Info
Incorrect Attempts:
CHECK
meters
Hint Unavailable
The vertical translation
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
meters
Hint Unavailable
= axis of symmetry.
Hint
Clear
Info
Incorrect Attempts:
CHECK
meters
Hint Unavailable
The period
Solution
period =
Hint
Clear
Info
Incorrect Attempts:
CHECK
minutes
Hint Unavailable
"One full ride around the wheel takes 4 minutes." The period is the time to complete one cycle. Therefore the period is 4 minutes.
period =
Hint
Clear
Info
Incorrect Attempts:
CHECK
minutes
Hint Unavailable
The 'k' value
Solution
k =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
k =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The equation of the trig function, H(t) with height starting at the bottom of the ferris wheel at t = 0.
Solution
H(t) =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
If the ferris wheel starts at the bottom, then height = 2m when t = 0.
H(t) =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Word Problems with Trig Functions: Clock
The hour hand on a clock rotates at 1 revolution per 12 hours. The clock has a diameter of 4cm and the point of interest to model is located at the tip of the hour hand, at the perimeter of the clock. Model the following using a sine function with start time at 12:00 noon.
The amplitude
Solution
a =
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
Amplitude = diameter / 2
= 2 cm
a =
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
= 2 cm
The period
Solution
T =
Hint
Clear
Info
Incorrect Attempts:
CHECK
hours
Hint Unavailable
The period (T) is the total time for one revolution, which is given as 12 hours.
T = 12 hours
T =
Hint
Clear
Info
Incorrect Attempts:
CHECK
hours
Hint Unavailable
T = 12 hours
The vertical translation
Solution
c =
Hint
Clear
Info
Incorrect Attempts:
CHECK
ƒ(x) = a·sin[k(x - d)] + c
If the axis of symmetry is located in the center of the clock, then the vertical translation could be assumed to be 0.
c =
Hint
Clear
Info
Incorrect Attempts:
CHECK
ƒ(x) = a·sin[k(x - d)] + c
The horizontal translation on a sin graph (assuming the hour hand starts at 12:00)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
hours
Hint Unavailable
Sketch the function and see that the that it is transformed from a parent function of sin by 3 hours to the left.
The horizontal translation would be -3, hours.
Hint
Clear
Info
Incorrect Attempts:
CHECK
hours
Hint Unavailable
The horizontal translation would be -3, hours.
The equation of the (sin) trig function.
Solution
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
ƒ(x) = a·sin[k(x - d)] + c
You need to determine the k-value for the equation:
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
ƒ(x) = a·sin[k(x - d)] + c
Word Problems with Trig Functions: Tides
Narragansett Bay has a maximum tide height 5m higher than the lowest point of 1m. A low tide point occurs at 2:00PM. If the time between adjacent high and low tides is 6 hours, 15 minutes, determine the following...
 |
The amplitude
Solution
a =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
amplitude
= (max - min)/2
= (6 - 1)/2
= (5)/2
= 2.5
a =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
= (max - min)/2
= (6 - 1)/2
= (5)/2
= 2.5
The k-value
Solution
k =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
"If the time between adjacent high and low tides is 6 hours, 15 minutes"... this is half a cycle. Therefore the period is double this... 12 hours and 30 minutes... 12.5 hours...
Period = 2π/k
12.5 = 2π/k
k = 2π/12.5
k = 4π/25
k =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Period = 2π/k
12.5 = 2π/k
k = 2π/12.5
k = 4π/25
The vertical translation
Solution
c =
Hint
Clear
Info
Incorrect Attempts:
CHECK
ƒ(x) = a·cos[k(x - d)] + c
c = (max + min)/2
= (6 + 1)/2
= (7)/2
= 3.5
c =
Hint
Clear
Info
Incorrect Attempts:
CHECK
ƒ(x) = a·cos[k(x - d)] + c
= (6 + 1)/2
= (7)/2
= 3.5
The horizontal translation, d (using a positive cos function, starting at 12:00 noon)
Solution
d =
Hint
Clear
Info
Incorrect Attempts:
CHECK
ƒ(x) = a·cos[k(x - d)] + c
If we are to use a cos function instead of a sine function, then we will use the maximum point of the tide as our starting point. We will set time as zero at 12:00 noon. So, with a low at 2:00PM there is a high tide 6 hours, 15 minutes later at 8:15PM. This is 8 hours, 15 minutes or 8.25 hours after noon. So, the horizontal translation will be 8.25 right
d = -8.25
d =
Hint
Clear
Info
Incorrect Attempts:
CHECK
ƒ(x) = a·cos[k(x - d)] + c
d = -8.25
The equation of the trig function
Solution
H(t) =
Hint
Clear
Info
Incorrect Attempts:
CHECK
H(t) = a·cos[k(t - d)] + c
H(t) = a·cos[k(t - d)] + c
=
H(t) =
Hint
Clear
Info
Incorrect Attempts:
CHECK
H(t) = a·cos[k(t - d)] + c
=
Word Problems with Trig Functions: Seasonal Temperatures
A function modelling the average temperature T, in degrees Celsius, in a certain ountry over the course of one year is given below where t is the time in days. Determine the following
The maximum temperature, and the month this occurs in. [3]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Maximum Temperature
= 16 + 13
= 29˚ Celsius
Solve to find this occurs in April.
The 190th day is ~ 6.3 months ~ June...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
= 16 + 13
= 29˚ Celsius
Solve to find this occurs in April. The 190th day is ~ 6.3 months ~ June...
What is the average temperature for the entire year?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
˚C
Think of the axis of symmetry
The average is the axis of symmetry, which is 13 (degrees Celsius).
Hint
Clear
Info
Incorrect Attempts:
CHECK
˚C
Think of the axis of symmetry
Predict the temperature on May 21st, the 140th day of the year.
Solution
T =
Hint
Clear
Info
Incorrect Attempts:
CHECK
˚C
Hint Unavailable
Substitute t = 140 into the equation...
This evaluates to 23.4 degrees Celsius.
T =
Hint
Clear
Info
Incorrect Attempts:
CHECK
˚C
Hint Unavailable
Trigonometric Equations and Identities
Equivalent Trigonometric Expressions
Given the cofunction identity,
sin23˚ is equivalent to:
Solution
sin(x˚)
= cos(90˚ - x˚)
= cos(90˚ - 23˚)
= cos(67˚)
= cos(90˚ - x˚)
= cos(90˚ - 23˚)
= cos(67˚)
is equivalent to cos( __ ) ?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Use the cofunction identity and make a common denominator:
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The following is correct.
Solution
The following is correct. If...
Solution
Then,
It is an equivalent horizontal shift, by a factor of pi,
Reflection in the Y-Axis (Even/Odd)
Which of the following is incorrect?
Solution
All of the above are reflections on the y-axis. The following is correct:
cos = cos
cos is the only trig function with symmetry on the y-axis.
Reflecting a graph of cos overlaps a graph of cos
cos = cos
cos is the only trig function with symmetry on the y-axis.
Reflecting a graph of cos overlaps a graph of cos
Equivalent Trigonometric Expressions
is equivalent to:
Solution
cos x... See that the two functions overlap (share the same coordinates) at some of the significant points (max, min, intercepts)...
is equivalent to:
Solution
Formula:
Solve,
is equivalent to:
Solution
Formulas used:
cancels because this is equivalent (periodic)
Simplify.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Formulas used:
Using the cofunction and co-related identities...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Exact Value with Compound Angle Formula (In Degrees and Radians)
Evaluate each of the following with an exact value, using the compound angle formulas.
| Angle (radians) | Angle (degrees) | sinx (exact value) | cosx (exact value) |
| 0˚ | = 0 | = 1 | |
| 30˚ | = | = | |
| 45˚ | = | = | |
| 60˚ | = | = | |
| 90˚ | = 1 | = 0 | |
| 180˚ | = 0 | = -1 | |
| 270˚ | = -1 | = 0 | |
| 360˚ | = 0 | = 1 |
cos(450˚)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Compound angle formula:
cos(x˚ + y˚) = (cos x˚)(cos y˚) - (sin x˚)(sin y˚)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
cos(x˚ + y˚) = (cos x˚)(cos y˚) - (sin x˚)(sin y˚)
sin(225˚)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Compound angle formula:
sin(x˚ + y˚) = (sin x˚)(cos y˚) + (cos x˚)(sin y˚)
Note this could also work or be done with sin(270˚ - 45˚)... you would get the same answer.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
sin(x˚ + y˚) = (sin x˚)(cos y˚) + (cos x˚)(sin y˚) Note this could also work or be done with sin(270˚ - 45˚)... you would get the same answer.
sin
Solution
Compound angle formula:
sin(x˚ - y˚) = (sin x˚)(cos y˚) - (cos x˚)(sin y˚)
sin(x˚ - y˚) = (sin x˚)(cos y˚) - (cos x˚)(sin y˚)
Compound Angle Formula (aka Addition Subtraction Formula)
Simplify the trig ratio cos(3x)cos(4x) - sin(3x)sin(4x)
Solution
Compound Angle Formula (aka Addition Subtraction Formula)
Compound angles can be evaluated by first converting each measure to an exact value.
Evaluate.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Use compound angle formula.
Compound Angle Formula (aka Addition Subtraction Formula)
Determine an equivalent expression to the following.
Solution
Compound Angle Formula (aka Addition Subtraction Formula)
Determine an equivalent expression to the following.
Solution
Compound Angle Formula (aka Addition Subtraction Formula)
Determine an equivalent expression to the following.
Solution
Compound Angle Formula (aka Addition Subtraction Formula)
Determine the exact value of
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Exact Value of Compound Angle Formula Using Principle Angles of Special Related Acute Angles
Evaluate each of the following with an exact value, using the compound angle formulas. These questions use the principle angles of related acute angles that are special triangle angles.
| Angle (degrees) | Related Special Acute Angle | sinx (exact value) | cosx (exact value) |
| 150˚ | 30˚ | = | = |
| 210˚ | 30˚ | = | = |
| 330˚ | 30˚ | = | = |
| 135˚ | 45˚ | = | = |
| 225˚ | 45˚ | = | = |
| 315˚ | 45˚ | = | = |
| 120˚ | 60˚ | = | = |
| 240˚ | 60˚ | = | = |
| 300˚ | 60˚ | = | = |
cos(285˚)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Use the compound angle formula: cos(x˚ + y˚) = (cos x˚)(cos y˚) - (sin x˚)(sin y˚)
You need to find combinations of angles that have 'Related Special Acute Angles' so you can lookup the exact values.
Note this could also work or be done with cos(60˚ + 225˚)... you would get the same answer.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
You need to find combinations of angles that have 'Related Special Acute Angles' so you can lookup the exact values. Note this could also work or be done with cos(60˚ + 225˚)... you would get the same answer.
Compound Angle Formula (aka Addition Subtraction Formula)
Determine the exact value of cos165˚
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Denationalized the denominator in cos45˚ and sin45˚
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Compound Angle Formula (aka Addition Subtraction Formula)
Determine the exact value of
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Compound Angle Formula (aka Addition Subtraction Formula)
Determine the exact value that is equivalent to the following.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Double Angle Formula Intro
Determine which one of the following is not a double angle formula.
Solution
There are 5 main double angle formulas...
Which of the following is incorrect?
Solution
Incorrect: sin2(x) = sin(x2)
Determine 2·sin2(x) given,
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Double Angle Formula & Compound Angle Formula (Derivation)
sin(4x) = sin(2x)sin(2x)
Solution
False. This is the double angle formula: sin(4x) = 2sin(2x)cos(2x)
sin(2x) = sin(x)cos(x) + sin(x)cos(x) = 2sin(x) · cos(x)
Solution
The double angle formula is derived partly using the compound angle formula, see:
The double angle formula just uses double or twice the angle in the trig, for example:
sin(2x), or cos(2x), or tan(2x).
The double angle formula just uses double or twice the angle in the trig, for example:
sin(2x), or cos(2x), or tan(2x).
Double Angle Formula
Given:
Determine tan(2θ)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Just use the double angle formula,
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Determine cos(θ) < 0
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
"cos(θ) < 0" means where cos is negative, using CAST, it is in Q3. (Sketch not shown)
Using special triangles, in Q3:
- x = -1
- y =
- r = 2
Solve:
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Using special triangles, in Q3:
- x = -1
- y =
- r = 2
Double Angle Formula
Evaluate with an exact answer.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
If cos(x) = , then cos(2x) = over the interval 0 ≤ x ≤ π.
Solution
False.
Given tan(x) = , determine sin(2x) and cos(2x) over the interval 0 ≤ x ≤ π. Reduce fully.
Solution
Hint
Clear
Info
sin(2x) = ━━cos(2x) = ━━
Incorrect Attempts:
CHECK
Hint Unavailable
First determine the other two ratios using reflex angle triangles on the CAST system, from 0 to π... This would be in quadrant 1 only. After making a sketch, you can determine that,
Next sub this into the double angle formulas to solve,
and,
furthermore,
Hint
Clear
Info
sin(2x) = ━━cos(2x) = ━━
Incorrect Attempts:
CHECK
Hint Unavailable
Evaluate over the interval 0 ≤ x ≤ π, giving exact answers. State your answers in increasing order.
sin(4x) = cos(2x)
Use the double angle formula on sin(4x),
The double angle, '2x' changes the interval from 0 ≤ x ≤ π, to 0 ≤ 2x ≤ 2π... Using a sketch of the cos function, and the CAST system...
There are 4 answers, in increasing order:
Double Angle Formula Identities
Determine an equivalent expression to the following.
Solution
Remember:
2sin(x) cos(x) = sin(2x)
2sin(x) cos(x) = sin(2x)
Solution
Solution
Pythagorean Identities
The identity, is correct at all points.
Solution
Video
True, for example at 0˚...
90˚...
and 180˚...
Determine sin(60˚), in terms of 'm' or 'n', given the following.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Using the CAST system, see that cos(300˚) = cos(60˚) because they share the same (acute) reflex angle, and are both positive (in quadrant 1 & 3).
Using the CAST system, see that cos(300˚) = cos(60˚) because they share the same (acute) reflex angle, and are both positive (in quadrant 1 & 3). So,
Enter answer as "1 - m^2"
Hint
Clear
Info
Incorrect Attempts:
CHECK
Using the CAST system, see that cos(300˚) = cos(60˚) because they share the same (acute) reflex angle, and are both positive (in quadrant 1 & 3).
Trig Identities
Prove the following identity:
Solution
Trig Identities
Solve for n in the following identity:
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Trig Identities
Prove the following identity:
Solution
Solving Trig Expressions
Solve the trig expression on the interval: 0 ≤ x ≤
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The interval given requires the -90˚ angle to be converted to the equivalent positive form, 270˚.
The interval given requires the angle to be stated in radians.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The interval given requires the angle to be stated in radians.
Solving Trig Equations
Solve on the interval: 0˚ ≤ x ≤ 180˚
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Cos is negative in quadrant II and quadrant III.
Since we are given the interval (0˚ ≤ x ≤ 180˚) we will only use quadrant II.
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Since we are given the interval (0˚ ≤ x ≤ 180˚) we will only use quadrant II.
Solving Trig Equations
Solve the trig equation on the interval: 0 ≤ x ≤
First, what is incorrect about the following solution? [1]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The interval and angle is given in radians, so you should state in radians when you evaluate.
Example:
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Example:
Now, solve the trig equation.
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solving Trig Equations
Round your answers to the nearest decimal place.
Solve the trig equation on the interval: 0 ≤ x ≤ .
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
radians
Hint Unavailable
The interval is in radians, so put your calculator in radians.
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
radians
Hint Unavailable
Solve the trig equation on the interval: 0 ≤ θ ≤ 360˚. Order from lowest to highest.
Solution
Hint
Clear
Info
θ1 = θ2 =
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Use CAST: sinθ is positive in Q1 & Q2 (sketch not shown), so using co-related angles...
Hint
Clear
Info
θ1 = θ2 =
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Solving Trig Equations
Solve for the exact value in degrees, on the interval: 0˚ ≤ x ≤ 90˚
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Solving Trig Equations
Solve using degrees, on the interval 0˚ ≤ x ≤ 360˚. Order your answers from lowest to highest.
Solution
Hint
Clear
Info
x1 = x2 = x3 = x4 =
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
In the function that equals zero, either of the following is zero:
(2sin x - 1) = 0
OR,
(cos2 x) = 0
sin(x) is positive,
using CAST and special triangles we get
x = 30˚, or 150˚
Use your understanding of a cos(x) graph.
cos(x) = 0 at the x-intercepts
x = 90˚, or 270˚
Hint
Clear
Info
x1 = x2 = x3 = x4 =
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
(2sin x - 1) = 0
OR,
(cos2 x) = 0
sin(x) is positive,
using CAST and special triangles we get
x = 30˚, or 150˚
Use your understanding of a cos(x) graph.
cos(x) = 0 at the x-intercepts
x = 90˚, or 270˚
Solving Trig Equations
Solve using degrees on the interval: 0˚ ≤ x ≤ 360˚. Order your answers from lowest to highest.
Solution
Hint
Clear
Info
x1 = x2 = x3 = x4 =
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Here we must factor by grouping (common factor the first two terms, then common factor the last two terms). This is the trickiest part of the question for most.
cos is negative in quadrant II and quadrant III
x = 150˚, 210˚
sin is positive in quadrant I and quadrant II
x = 60˚, 120˚
Hint
Clear
Info
x1 = x2 = x3 = x4 =
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
x = 150˚, 210˚ sin is positive in quadrant I and quadrant II
x = 60˚, 120˚
Solving Trig Equations
Solve using degrees on the interval: 0˚ ≤ x ≤ 360˚. Order your answers from lowest to highest.
Solution
Hint
Clear
Info
x1 = x2 = x3 = x4 =
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
It may be tricky to see that this is a difference of squares!
tan is positive in quadrant I and quadrant III
x = 30˚, 210˚
tan is negative in quadrant II and quadrant IV
x = 150˚, 330˚
Hint
Clear
Info
x1 = x2 = x3 = x4 =
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
x = 30˚, 210˚ tan is negative in quadrant II and quadrant IV
x = 150˚, 330˚
Solving for the Trig Equation
Determine the quadratic equation, in standard form, that would evaluate to x = 240˚ and 300˚ on the interval 0˚ ≤ x ≤ 360˚.
Solution
240˚ and 300˚ both have related acute angles of 60˚
Located in quadrant III and IV, where sin is negative...
Put into factored form of quadratic equation and foil to get standard form:
Located in quadrant III and IV, where sin is negative... Put into factored form of quadratic equation and foil to get standard form:
Solving Trig Equations with Various Arguments
Solve for the interval: 0˚ ≤ x ≤ 90˚. Order your answers from low to high.
Solution
Hint
Clear
Info
x1 = x2 =
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
(Common Mistake) Remember, because the angle is '2x', the interval changes by the same factor, 2,
0˚ ≤ x ≤ 90˚ ---> 0˚ ≤ 2x ≤ 180˚
Using CAST: see that sin(x) is positive in Q1 & Q2.
And the principle angles in Q1 & Q2 are,
Hint
Clear
Info
x1 = x2 =
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Solve for the interval: 0˚ ≤ x ≤ 1,080˚. Order your answers from low to high.
Solution
Hint
Clear
Info
x1 = x2 = x3 =
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
(Common Mistake) Remember, because the angle is , the interval changes by the same factor, divide by 2,
0˚ ≤ x ≤ 1080˚ --->
Using CAST: see that tan(x) is positive in Q1 & Q3. (sketch not shown) See that this is special triangles with 'x' = 1, 'y' = , and 'r' = 2, with the reflex angle of 60˚
Now find all other (principle) angles, including co-terminal angles up to 540˚
Hint
Clear
Info
x1 = x2 = x3 =
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Solving Trig Equations
Solve using degrees, on the interval 0˚ ≤ x ≤ 360˚, and determine the total number of answers.
Solution
It may be tricky to see that this is a difference of squares!
Tan is negative in quadrant II and IV, and positive in quadrant I and III.
Polynomial Trig Equations
Solve over the interval 0˚ ≤ θ ≤ 360˚. State your answers in increasing order.
Solution
Hint
Clear
Info
θ1 = θ2 =
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Simplify,
Let x = sinθ
Using polynomial long division (not shown)...
Sub back, x = sinθ
Now do each 'CAST' separately to determine the principle angles over the given interval (sketches not shown)...
Hint
Clear
Info
θ1 = θ2 =
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Exponential & Logarithmic Functions
Log Basics
Match the correct pairs:
Solution
log(0)
log(1)
log(10)
log(100)
= 0
= 1
= 2
= Undefined
log(1 × 10n) = n
log(0)
log(1)
log(10)
log(100)
= 0
= 1
= 2
= Undefined
Log Basics
True or false?
Solution
For example...
The log you normally see most often has a base 10...
Generally,
Same is even for non-base 10 logs, for example,
The log you normally see most often has a base 10... Generally, Same is even for non-base 10 logs, for example,
True or false?
Solution
Notice the trend, and match the correct answers to the following logs.
Solution
Log Laws
Use your understanding of basic log law theory to answer the questions...
Which of the following is not true?
Solution
for all values of 'a' because a0 = 1.
All of the following are undefined except for which one of the following log expressions?
Solution
The following are undefined:
Know that the log of zero and the log of a negative number are both undefined.
Know that the log of zero and the log of a negative number are both undefined.
Which of the following is not a logarithm law?
Solution
These 3 are the common misconceptions about log laws.
Use the following correct laws:
log(ab) = log(a) + log(b)
log(a/b) = log(a) - log(b)
Use the following correct laws:
log(ab) = log(a) + log(b)
log(a/b) = log(a) - log(b)
Logarithmic Expressions
Evaluate.
| Log Laws |
| loga(1) = 0 |
| loga(a) = 1 |
| a(logab) = b |
| loga(ab) = b |
| -log(a) = log(1/a) |
| log(ab) = log(a) + log(b) |
| log(a/b) = log(a) - log(b) |
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Make 'b' and 'a' the same in: logba
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Learning Logs, Practice
Arrange the solution steps shown here into the correct order (by dragging them).
Solution
The square root of 7 can be written as an exponent:
The exponent in a log comes down and multiplies in-front of the log:
If the base of a log is the same as the number in brackets, this always equals 1:
Logarithmic Equations
Solve.
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Remember, if it's not shown, the log is assumed to be base 10.
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
10
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
10
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Logarithmic Equations 2
Evaluate.
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
x =
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
x =
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
x =
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
Careful, a COMMON MISTAKE is to think the following is true:
x =
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
x =
Hint
Clear
Info
━━ ,
Incorrect Attempts:
CHECK
Hint Unavailable
x =
Hint
Clear
Info
━━ ,
Incorrect Attempts:
CHECK
Hint Unavailable
Log Expressions
Evaluate.
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Evaluate.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Exponent Laws with Equations
Solve.
Solution
Video
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Video
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
See this is in the form of a quadratic...
Let ... then factor...
Sub back in and solve for x...
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Log Law Practice
Solve the following, to practice log laws with algebra.
Logs in logs...
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Peel off the layers of logs, working from the outside to the inside.
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solve the expression below, given 20a = 5 and 5b = 100.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
First rearrange for 'a' and 'b'
Then substitute,
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Change of Base of a Logarithm
For logb(a), 'b' is called the base, and 'a' is called the argument, or sometimes the parameter.
True or false?
Solution
These are all the same, it doesn't matter what base is chosen.
According to the change of base formula below, -2log5(12) is equal to which of the following?
Evaluate log4(23) to the nearest tenth decimal place.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Basically, it's impossible to type a non-base-10 log into the calculator. So you need to change the base to base 10 first, and then type into the calculator.
Use change of base formula and plug into calculator.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Use change of base formula and plug into calculator.
Determine the value of 4x2, given,
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Use change of base formula on the first part,
Then plug into...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solve for 'x'.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Here is one way of doing it, by changing the bases to '8'
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Change of Base of a Logarithm with Reciprocals
True or false?
Solution
Work it out, using the change of base as you know it.
In your own notes, show that for m, n > 1:
Solution
Applying the change of base on both,
In your own notes, show that:
Solution
Need to change bases first,
In your own notes, show that (for b > 0, ≠ 1, and n > 0):
Solution
Apply change of base,
Change of Base of a Logarithm with Perfect Squares or Cubes
Show, using the equation given below that,
Solution
Remember the form of perfect cubes,
So make the perfect cube with insertion,
Take the log of both sides and rearrange,
Change of Base Formula Derivation
Given the change of base formula,
Using the given variables, derive the change of base formula from, . Show your work in your own notes.
Solution
Like many, this one is only tricky if you don't know the steps
First, let:
Then, take the log (with base 'b') of both sides
First, let: Then, take the log (with base 'b') of both sides
Solving Logarithmic Equations
The following can be solved as:
Solution
Solve.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Use change of base...
Let b = ...
So,
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Word Problems: Bacteria
A colony of bacteria doubles every n number days according to the function below. If the colony starts with 88 bacteria and turns into 22,528 in 20 days, determine the doubling time of the colony.
Solution
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
days
Hint Unavailable
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
days
Hint Unavailable
Word Problems: Decibel Sound Intensity
Sound intensity is measured in units of decibels (dB), where 'I' is sound intensity and 'I0' is a reference intensity of the threshold of our hearing ability.
A car crash is typically 145 dB, while the airbag is typically 165 dB. How many times more intense is the sound of the airbag than the sound of the crash itself?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
times
Hint Unavailable
First rearrange the equation for intensity 'I' using log laws
Then determine the ratio, using exponent laws
The airbag is 100 times more intense sounding than the crash.
Hint
Clear
Info
Incorrect Attempts:
CHECK
times
Hint Unavailable
Natural Log and Natural Exponential (Base 'e')
'e' is a real number, approximately equal to 2.71828, that is a base of natural logarithms.
ln(e) = 1
Solution
The natural logarithm (ln) of e is always 1.
ln(10) = log(10)
Solution
Becareful not to confuse the natural logarithm (ln) with the base-10 logarithm (log).
Solve.
Solution
Solve.
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solve. Round your answer to the nearest hundredth decimal place.
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
So, either,
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Natural Log Word Problem
The metabolism of a certain drug by the average male is given by k = 0.1234 hr-1. If the initial concentration is 9 mg/L and the final concentration is 0.5 mg/L, determine the time it takes.
Solution
ln[A]f = -kt + ln[A]i
t =
Hint
Clear
Info
Incorrect Attempts:
CHECK
hours
Hint Unavailable
t =
Hint
Clear
Info
Incorrect Attempts:
CHECK
hours
Hint Unavailable
Word Problems with Logs
$10,000 is invested at 3% annually over a certain number of investment periods, n. If the final value is $11,592.74 determine the number of periods n.
Solution
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
periods
Hint Unavailable
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
periods
Hint Unavailable
Graphing Logarithmic Functions
The functions and are equivalent.
Solution
Using log laws it can be shown that =
Graphing Logarithmic Functions
The reciprocal of the function equals
Solution
The inverse of the function equals
x = ay equals y = loga(x)
The reciprocal of equals
x = ay equals y = loga(x)
The reciprocal of equals
Graphing Logarithmic Functions
Which of the following is the inverse of the function ?
Solution
Switch 'x' and 'y' and then isolate for 'y'.
Using the change of base formula,
Graphing Logarithmic Functions
Prove that the following functions are inverse using the coordinate (1, 3).
Solution
Inverse functions switch 'x' and 'y' in the coordinates (a, b) ↔ (b, a).
Therefore the above functions are inversely related.
Graphing Logarithmic Functions
The x-intercept of the function y = log(x) occurs at:
Solution
Note the log law:
The x-intercept always occurs when y = 0
The log of 1 is always zero.
In other words, the x-intercept occurs at (1, 0).
The x-intercept always occurs when y = 0
The log of 1 is always zero. In other words, the x-intercept occurs at (1, 0).
Graphing Logarithmic Functions
The vertical asymptote of y = log(x) occurs at x = 0.
Solution
True, see:
Graphing Logarithmic Functions
Describe the transformations on the function:
Graphing Logarithmic Functions
Transform y = log(x) to produce a function with the following transformations
Solution
Vertical stretch by a factor of 3
Reflection in the y-axis
Horizontal stretch by a factor of 2
Horizontal translation 4 units right
Vertical translation 1 unit up
Graphing Logarithmic Functions
Which property do the following functions all have in common?
Solution
They all have a vertical asymptote at x = 0...
Graphing Logarithmic Functions
Which one of the following functions does not have the same domain as the others?
Solution
All have the domain {xεR, x > 0} except the function that has the domain {xεR, x > -1} because it is translated 1 unit left, which changes the location of the vertical asymptote.
Graphing Logarithmic Functions
Determine the exact value of the x-intercept of the function .
Solution
x =
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
The x-intercept occurs at y = 0.
x =
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Working with Log Equations
Solve, rounding your answer to the nearest hundredth.
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
For an in initial investment of a certain amount (A0) at a certain rate (R) over a certain amount of time (t), different compounding periods (n) will have a very small difference in the final amount (A) of an investment.
The following are approximately equivalent:
"If you put $1 into a bank account paying 100% interest compounded continually, at the end of the year, you’ll have exactly e dollars."
A $100.00 investment is turned into $112.75 over a 3 year period. If the interest rate is compounded monthly, calculate the interest rate.
Solution
rate =
Hint
Clear
Info
Incorrect Attempts:
CHECK
%
Hint Unavailable
Cannot solve for rate with the equation:
This equation must be used when solving for rate:
(Notice that the compounding period is not used)
rate =
Hint
Clear
Info
Incorrect Attempts:
CHECK
%
Hint Unavailable
This equation must be used when solving for rate: (Notice that the compounding period is not used)
Rates of Change of Functions
Rates of Change
Which of the following scenarios would have a constant, positive average rate of change?
Solution
A positive rate of change has a positive slope. A constant average rate of change has the same magnitude of slope for all intervals of 'x'.
Instantaneous and Average Rates of Change
Given the function ƒ(x) = x4 - x3, find:
the average rate of change on the interval -3 ≤ x ≤ 1
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
the instantaneous rate of change at x = -5
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Instantaneous Rate of Change at the Vertex of a Quadratic Function (Without Difference Quotient)
For the function ƒ(x) = 3(x - 4)2 + 1
Estimate the instantaneous rate of change at the vertex, without using difference quotient.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint: Slope at the vertex point.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint: Slope at the vertex point.
Determine the average rate of change from x = 2 to x = 8.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Exact Instantaneous Rate of Change using the Difference Quotient
Given the function ƒ(x) = 2x - 4x2, find the slope of the tangent using the difference quotient, at x = -2.
Solution
m =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
m =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Exact Instantaneous Rate of Change using the Difference Quotient
A baseball is launched into the air and its height can be modelled by the function h(t) = -5t2 + 15t + 1, where h(t) is height in metres, and t is time in seconds. Determine the exact instantaneous rate of change in the height of the baseball at 2s.
Solution
s =
Hint
Clear
Info
Incorrect Attempts:
CHECK
m/s
Hint Unavailable
Givens:
t = 2.0 s
h = 0.01
For a small 'h' = 0.01 approaching zero,
Now substitute into the original equation, and solve,
s =
Hint
Clear
Info
Incorrect Attempts:
CHECK
m/s
Hint Unavailable
t = 2.0 s
h = 0.01 For a small 'h' = 0.01 approaching zero, Now substitute into the original equation, and solve,
Verify if a Maximum or Minimum Exists at a Given Point Using Estimation of Instantaneous Rate of Change
Given the function ƒ(x) = x2 - 4x + 5, verify and state if a maximum or minimum occurs at the point (2, 1). [1]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Verify Whether a Point is either a Maximum or a Minimum
Given that a point of inflection occurs at x = -2 for the following function, ƒ(x) = 2x3 + 7x2 + 4x, verify and state whether the point is a maximum or a minimum. [1]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Rates of Change with Trig Functions
Average Rate of Change for a Trig Function
For the function ƒ(x) = 8sin(x), calculate the exact value of the average rate of change on the interval [0, 90]
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Estimating Instantaneous Rate of Change for a Trig Function
For the function ƒ(x) = 6sin(30x) + 10, calculate the instantaneous rate of change at x = 2
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Combinations & Compositions of Functions
Combination & Composition Operations and Notation
Given the functions:
f(x) = 3x + 2g(x) = -5x2 - 2x
The functions can be combined in which way?
Solution
Functions can be combined with any of the operations listed in the question. You will see examples of this later on.
ƒ ∘ g is equivalent to which two of the following operations or notations?
Solution
The following are equivalent:
ƒ ∘ g = (ƒ ∘ g)(x) = f(g(x))
The following are equivalent:
(f × g)(x) = f(x) × g(x)
Combination and Composition with Tables of Values
Determine each of the following, using the table given below.
| x | g(x) |
| -4 | -30 |
| -2 | -10 |
| -1 | -3 |
| 0 | 0 |
| 1 | -5 |
| 2 | 30 |
| 3 | -135 |
| x | ƒ(x) |
| -3 | 5 |
| -2 | 0 |
| -1 | -3 |
| 0 | -4 |
| 1 | -3 |
| 2 | 0 |
| 3 | 5 |
g(1) + f(3)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(ƒ + g)(0)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(g × f)(1)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(ƒ ◦ g)(0)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(g ◦ ƒ ◦ ƒ)(-2)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Composition with Tables of Values
Determine the set (of coordinates) contained within the composition ƒ[g(x)].
Solution
x g(x)
-2 1
-1 5
0 -4
1 -3
2 0
3 4
x ƒ(x)
-2 2
-1 3
0 6
1 17
2 23
3 12
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The set (of coordinates) contains the points with the 'x' value from g(x) and the 'y' value from f(x), in the form: (xg, yf). This comes from the points that share the same 'y' value from g(x) substituted as 'x' for f(x)...
Since,
f[g(-2)] = 17
And,
f[g(2)] = 6
Then the set is:
{(-2, 17), (2, 6)}
| x | g(x) |
| -2 | 1 |
| -1 | 5 |
| 0 | -4 |
| 1 | -3 |
| 2 | 0 |
| 3 | 4 |
| x | ƒ(x) |
| -2 | 2 |
| -1 | 3 |
| 0 | 6 |
| 1 | 17 |
| 2 | 23 |
| 3 | 12 |
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Compositions as Substitution
For the functions,
Determine f(g(0))
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Determine g(f(x))
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Combinations
Determine whether the following is true or false.
Solution
(ƒ — g)(x) = ƒ(x) — g(x)
This is combination notation.
If n(x) = 12 and m(x) = 6, then (n + m)(x) = 16.
Solution
Determine the following, given ƒ(x) = 4x + 2 and g(x) = 2sinx.
Solution
(ƒ - g)(45)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Combine the functions first, (ƒ - g)(x) = ƒ(x) - g(x), then substitute the independent value,
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Combinations: Product, Trig
Given (ƒ × g)(x) = 8x sinx + 4sinx, what are two possible values of ƒ(x) and g(x)?
Solution
Domain of Combinations
Which statement is true about the domain of all combinations of functions (added, subtracted, multiplied, or divided).
Solution
You know that domain is the range (or region) of independent values that can exist for a function. The domain of a combination of functions will be determined by the shared region of 'x' that exists.
If the domain of function 1 is {XER | 1 ≤ x} and the domain of function 2 is {XER | x ≤ 10}, then the domain of the combined function is {XER | 1 ≤ x ≤ 10}.
Solution
The combined domain is the region of x that is shared by both functions.
State the domain for the (ƒ × g)(x) of the following functions, using proper set notation.
Solution
ƒ(x) = sin(x)
g(x) = log(x)
Hint
Clear
Info
Domain:
Incorrect Attempts:
CHECK
Hint Unavailable
The domain of ƒ(x) = sin(x + 2) is {XER}
The domain of g(x) = log(x) is {XER | x > 0}
So the combined domain is {XER | x > 0}.
Hint
Clear
Info
Domain:
Incorrect Attempts:
CHECK
Hint Unavailable
The domain of g(x) = log(x) is {XER | x > 0}
So the combined domain is {XER | x > 0}.

Domain of Compositions
Which of the following compositions have the same domain for (ƒ ◦ g)(x) and (g ◦ f)(x)?
Solution
None of the functions have the same domain. Some may think that and have the same domain but, the domain of is {XER: x ≥ 0} and the domain of is {XER}. [Both have the same range, {YER: y ≥ 0}]
As an aside: and should have the same domain, {XER}
As an aside: and should have the same domain, {XER}
Solving Combination of Functions (Intersection)
The point of intersection of two functions can be solved with guess and check.
Solution
1st set the equations equal.
2nd guess a value of x that makes it close to LS = RS
3rd Sub x into your equation to solve for y and the point.
2nd guess a value of x that makes it close to LS = RS
3rd Sub x into your equation to solve for y and the point.
Combinations
Determine which of the following functions could create the look:
Solution
It looks like a trig function that is increasing exponentially.
Combination with Division (Quotient)
The (ƒ ÷ g)(x) will have restrictions based on the value of x in g(x).
Solution
When g(x) is in the denominator, the combined function will have restrictions on all values of 'x' for which g(x) equals zero.
State the domain on the combination of (f ÷ g)(x) where,
Solution
ƒ(x) = 2x + 3
g(x) = log(x)
log(x) ≠ 0, so x ≠ 1
log(x) > 0, so x > 0
(interestingly in this case, there is a restriction in a restriction.)
The domain is: {XER | 0 < x < 1, x > 1}
{XER | x ≠ 0, 1} is not considered correct because 'x' cannot be negative.
log(x) > 0, so x > 0
(interestingly in this case, there is a restriction in a restriction.)
The domain is: {XER | 0 < x < 1, x > 1}
{XER | x ≠ 0, 1} is not considered correct because 'x' cannot be negative.
Composition of Functions
Two functions are defined:
(ƒ ∘ g)(x) always equals (g ∘ ƒ)(x)
Solution
Rarely, but this is called commutation when: (ƒ ∘ g)(x) = (g ∘ ƒ)(x)
Determine which of the following would be (ƒ ∘ g)(x)
Solution
Evaluate (ƒ ∘ g)(3)
Solution
(ƒ ∘ g)(3) =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(ƒ ∘ g)(3) =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Evaluate (ƒ ∘ g ∘ ƒ)(x)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
This is equivalent to
So,
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Evaluate [ƒ ∘ g(x)] ∘ ƒ(-5)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
First evaluate ƒ ∘ g(x),
So [ƒ ∘ g(x)] ∘ ƒ(-5) becomes,
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Composition of Functions
Determine the function ƒ(x), in standard form, x2 + bx + c, given,
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
Since there is a degree of two (x2) within f[g(x)], then try the following form with the constants 'j' and 'k',
So, either,
So, f(x) equals,
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
Determine the function c(x), given,
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
First determine a[b(x)],
Let c(x) = a
So, either,
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Composition of Functions with Inverse
Given the equation
ƒ(x) = 3x + 4Determine the inverse (f-1).
Solution
ƒ-1(x) =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
ƒ-1(x) =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Determine (ƒ ∘ ƒ-1).
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Determine (ƒ-1 ∘ ƒ).
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
For any function and its inverse, ƒ(x) and ƒ-1(x) the following is true:
Solution
(ƒ ∘ ƒ-1) = (ƒ-1 ∘ ƒ) = x
Be careful not to confuse 'inverse' with 'reciprocal'
True, for any function and its inverse:
(ƒ ∘ ƒ-1) = (ƒ-1 ∘ ƒ) = x
True, for any function and its inverse: (ƒ ∘ ƒ-1) = (ƒ-1 ∘ ƒ) = x
Determine (ƒ ∘ ƒ)-1.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
First, determine ƒ ∘ ƒ
Next, determine (ƒ ∘ ƒ)-1
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Composition of Functions
Determine two possible functions, m(x) and n(x) that compose to form p(x) = 23x + 4
Solution
(Answers may vary)
One possible answer is:
Sub n(x) into m(x) to get p(x).
One possible answer is: Sub n(x) into m(x) to get p(x).
Combination of Functions with Unknowns
The two points (-1, -24), (-3, 0) lie on the combined function of, (n × m)(x). Determine the values, 'a' and 'b'.
Solution
n(x) = 2x2 + ax - 3
m(x) = bx2 - 5x + 3
Hint
Clear
Info
a = b =
Incorrect Attempts:
CHECK
Hint Unavailable
- The domain of the combined function is shared (the same) for both n(x) and m(x).
- This allows us to use the 'x' value from the combined function, '-1' and '-3', and substitute into both n(x) and m(x).
- We do this to get the 'y' values for n(x) and m(x).
- For the combined function, (n × m)(x), the 'y' values multiply so that: yn × ym = ycombined.
- We show this below.
Substitute the 'x = -1' into the equations for n(x),
And the 'x = -3', into m(x),
The combination of functions, (n × m)(x), is the product of the 'y' values of n(x) and m(x), yn × ym = ycombined:
Substitute one equation for another. You can isolate for 'a' in one equation
And substitute it into the other,
Plug in each 'b' value into one of the previous equations to solve for 'a'
Therefore, b = -4, and a = 5
[b ≠ -2 since 'a' is undefined for that value].
Hint
Clear
Info
a = b =
Incorrect Attempts:
CHECK
Hint Unavailable
- The domain of the combined function is shared (the same) for both n(x) and m(x).
- This allows us to use the 'x' value from the combined function, '-1' and '-3', and substitute into both n(x) and m(x).
- We do this to get the 'y' values for n(x) and m(x).
- For the combined function, (n × m)(x), the 'y' values multiply so that: yn × ym = ycombined.
- We show this below.
[b ≠ -2 since 'a' is undefined for that value].
