GRADE
10
Principles of Math MPM2D
TABLE OF CONTENTS
Linear Systems
Solution to a System
The solution to a system is the point of intersection.
Solution
'Solve the system' means find the point of intersection (POI). The solution to the system is the POI.
Solutions
Match the systems to their number of solutions.
Solution
0 (no) solution
1 solution
2 solutions
Infinite solutions
A system has 0 (no) solution when the lines are parallel (same slope).
Infinite solutions occur when the lines overlap (collinear).
1 solution is 1 point of intersection.
Infinite solutions occur when the lines overlap (collinear).
1 solution is 1 point of intersection.
Solving Linear Systems with Elimination
Solve the system using elimination.
Solution
Hint
Clear
Info
x = y =
Incorrect Attempts:
CHECK
Hint Unavailable
Sub 'x' into an equation to solve for 'y'
The solution to the system is the point of intersection, POI: (2, 2)
Solution
Hint
Clear
Info
x = y =
Incorrect Attempts:
CHECK
Hint Unavailable
Then solve for x (not shown)... x = 1
Solution
Hint
Clear
Info
a = b =
Incorrect Attempts:
CHECK
Hint Unavailable
Then solve for b when a = 3
Solving Linear Systems with Substitution
Solve the system using substitution.
Solution
Hint
Clear
Info
x = y =
Incorrect Attempts:
CHECK
Hint Unavailable
Sub 'y' into equation 2:
Determine the other value:
The point is (17, 38)
Solution
Hint
Clear
Info
x = y =
Incorrect Attempts:
CHECK
Hint Unavailable
Sub equation 1 into equation 2 to solve for x:
Find 'y'
the point is: (2, -3)
Linear System Theory
Explain why the following linear system has no solution. [1]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Systems have no solution when the lines are parallel.
Determine the slope in the form:
y = mx = b
Determine the slope in the form: y = mx = b
Practice Solving Linear Algebra
Solve.
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Linear Systems with Fractions
Solve the following system, using any method
Solution
Video
Hint
Clear
Info
x = y =
Incorrect Attempts:
CHECK
Hint Unavailable
Simplify equation ①
Simplify equation ②
Convert equation ① × 3 and equation ② × 5 for elimination...
Using elimination solve for y...
Solve for x...
Linear System Word Problems
Solve.
[Geometry] In triangle ABC, angle B is 20 less than three times angle A, and angle C is 20 more than two times angle A. Find the angles A, B, and C.
Solution
Hint
Clear
Info
A = B = C =
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
- Let angle A be 'A'
- Let angle B be 3A - 20
- Let angle C be 2A + 20
Angle B,
Angle C,
- Let angle A be 'A'
- Let angle B be 3A - 20
- Let angle C be 2A + 20
[Proportions] A 4.0 L solution contains 20% alcohol, and is mixed with an 8.0 L solution that is 50% alcohol. What percent of the resulting mixture is alcohol?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
%
Hint Unavailable
Percent alcohol is the total amount of alcohol,
... divided by the total volume,
[Money] For a concert, Sarah decides to order T-shirts for all of the participants. It costs $4 per shirt for the medium size, and $5 per shirt for the large size. Sarah orders a total of 70 T-shirts and spends $320. How many are medium shirts? Solution
 |
- Let 'x' be the number of medium shirts
- Let 'y' be the number of large shirts
- The amount of money made from each shirt type is (# sold)(price)
[Money Alternate] Jeremy and Sarah have a combined income of $80,000. One quarter of Jeremy's income is the same as one-sixth of Sarah’s income. How much does each person earn?
Solution
Hint
Clear
Info
Jeremy: $ Sarah: $
Incorrect Attempts:
CHECK
Hint Unavailable
- Let 'x' be Jeremy's income
- Let 'y' be Sarah's income
Equation ①
Equation ②
Solve substituting ① into ②...
Solve for 'y'...
- Let 'x' be Jeremy's income
- Let 'y' be Sarah's income
[Distance, Speed, Time] A train leaves Town A and heads for Town B at an average speed of 45 km/hr. A second train leaves Town B at the same time and heads for Town A at an average speed of 30 km/hr. If the route is 450 km long, then how many hours will it take for the two trains to meet?
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
hours
Hint Unavailable
Write the givens (d, s, t) in a table to organize...
Train A Train B
Distance x 450km - x
Speed 45 km/h 30 km/h
Time t t
Notice the time for Train A equals time for Train B...
The distance Train A travels is 270km... Now calculate the time for train A...
Train A (and Train B) take 6 hours to meet.
| Train A | Train B | |
| Distance | x | 450km - x |
| Speed | 45 km/h | 30 km/h |
| Time | t | t |
[Alternate Distance, Speed, Time] A boat took 5.0 hours to travel 60 km up a river against the current. The return trip took 3.0 hours. Find the speed of the boat in still water and the speed of the current.
Solution
Video
Hint
Clear
Info
Boat speed: Current speed:
Incorrect Attempts:
CHECK
km/hr
Hint Unavailable
Make a table to organize the distance, speed, and time for the upstream and downstream trips...
Let 'b' be the speed of the boat, and 'c' the speed of the current.
Upstream Downstream
Distance (km) 60 km 60 km
Speed (km/h) b - c b + c
Time (h) 5 h 3 h
Make an equation for d = s × t for the upstream trip...
Make an equation for d = s × t for the downstream trip...
Multiply ① × 3 and ② × 5 for elimination...
Eliminate the c's to solve for 'b', by adding ② & ①...
Then, solve for c...
Let 'b' be the speed of the boat, and 'c' the speed of the current.
| Upstream | Downstream | |
| Distance (km) | 60 km | 60 km |
| Speed (km/h) | b - c | b + c |
| Time (h) | 5 h | 3 h |
[Proportions] If a nickel costs the US mint 9.4 cents to make and a dime costs 4.6 cents, determine the unit cost of nickel and copper, given the information below.
Solution
- A nickel weighs 5 grams and is 25% nickel and 75% copper
- A dime weighs 2.268 grams and is 8.33% nickel and 91.67% copper
Hint
Clear
Info
Unit cost nickel: ¢
Unit cost copper:
¢
Incorrect Attempts:
CHECK
Hint Unavailable
- Let 'x' be the cost of nickel (per unit mass)
- Let 'y' be the cost of copper (per unit mass)
- The mass amount of a specific metal is the mass of the whole coin times the ratio proportion.
- The total cost of the metal is the mass amount times the cost (per unit mass)
Equation ① for the nickel coin,
Equation ② for the dime coin,
Solve using substitution... Rearrange ①...
Substitute into equation ②...
Solve for 'y'
- Let 'x' be the cost of nickel (per unit mass)
- Let 'y' be the cost of copper (per unit mass)
- The mass amount of a specific metal is the mass of the whole coin times the ratio proportion.
- The total cost of the metal is the mass amount times the cost (per unit mass)
Analytic Geometry
Line Segments
Explain the difference between a right bisector and an altitude. [3]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Equation of a line given two points
Determine the equation of the line connecting the two points, D(-2, 1) and G(2, 10). (Reduce improper fractions fully).
Solution
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Equation of the right bisector of a line given two points
Determine the equation of the right bisector of a line connecting the two points T(-8, 6) and U(2, 10). (Reduce improper fractions fully).
Solution
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Find equation of a right bisector and verify if a point lies on the line.
Does the point P(-3, -2) lie on the right bisector of the line segment with endpoints Q(-2, 5) and R(4, 1)? Justify your answer, by showing your work in your notes.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Pre - Length of a line formula
The distance between two points can be calculated as the hypotenuse using the Pythagorean theorem. Given the two points A(1, -5) and B(3, n)...
Use the Pythagorean theorem to determine the distance between the two points, in terms of n.
Solution
Use a sketch to visualize/determine the change in x and the change in y...
∆ x = 3 - 1 = 2
∆ y = n - (-5) = n + 5
Calculate hypotenuse length (distance), c...
∆ x = 3 - 1 = 2
∆ y = n - (-5) = n + 5
Calculate hypotenuse length (distance), c...
Now, calculate the length of the line between these two points using the distance formula below, in terms of n.
Solution
Make A(1, -5) point 1, and B(3, n) point 2.
x1 = 1
y1 = -5
x2 = 3
y2 = n
Takeaway: See that the distance (length) of a line equation is based on the same idea as the Pythagorean theorem. It is important to understand this before you jump into the distance (length) of a line equation, so you know where it comes from.
x1 = 1
y1 = -5
x2 = 3
y2 = n
Takeaway: See that the distance (length) of a line equation is based on the same idea as the Pythagorean theorem. It is important to understand this before you jump into the distance (length) of a line equation, so you know where it comes from.
Pre - Length of a line formula basics
True or false?
Solution
This is true because the square of the differences for example, (5 - x)2 or (x - 5)2, becomes the same positive magnitude...
Which of the following operations is/are correct?
Solution
II is wrong because when there are more than one term underneath the square root, then the root and squares no longer cancel. The root only cancels the squares when there is one square term underneath (example I).
Length of a line formula
On a street map, the coordinates of the two fire stations in a town are A(10, 63) and B(87, 30). A neighbor reports smoke coming from the kitchen of a house at C(41, 18). Which fire station is closer to this house? Solution
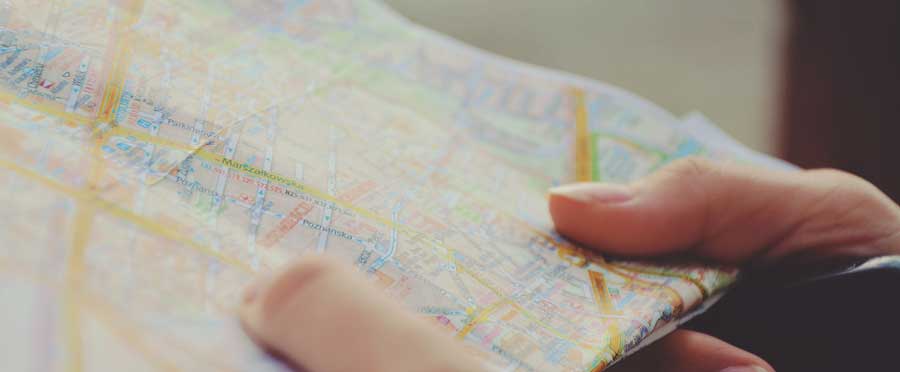 |
Two firestations are located at A(-10, -3) and B(6, -9). Station A is old with an outdate line of 'Firemobile' firetrucks that can only safely go a top speed of 40 km/h in city traffic. Station B is a completely new station with new 'FS1' firetrucks with GPS, AWD, and ABS technology and that can safely go a top speed of 65 km/h in city traffic. There is a fire at F(-4, 5) where the coordinates are in kilometers. Determine the outcome assuming everything runs smoothly.
Solution
Determine the distance of the fire from station A...
Determine the distance of the fire from station B...
Time for Firemobile from station A...
Time for FS1 from station B...
Therefore Firemobile trucks from station A arrive first.
Perpendicular lines, solving systems, and length of a line segment.
A line connects points X(1, 2) and Y(5, 7). A third point Z(-2, 8) is located nearby.
Determine the equation of the line connecting XY.
Solution
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solve the system of the two perpendicular lines, XY and the perpendicular line from Z, ie. determine the point of intersection (POI). Simplify fully.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Calculate the shortest distance from point Z to the line XY.
Solution
d =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Equal Segments (Distances)
Determine the coordinates of the two points that split the line connecting the points (10, 20) and (37, 8) into three equal segments.
Solution
Hint
Clear
Info
(19, ) & ( , )
Incorrect Attempts:
CHECK
Hint Unavailable
The total difference in 'x' is...
The 3 equal segments have distances in 'x'...
The total difference in 'y' is...
The 3 equal segments have distances in 'y'...
The two points are: (19, 16) & (28, 12).
∆ = +9: 10 ↔ 19 ↔ 28 ↔ 37
∆ = -4: 20 ↔ 16 ↔ 12 ↔ 8
Equation of a Circle at the Origin
Determine whether or not the point P(√35, 2) lies inside, outside, or on the perimeter of the circle defined by the function...
Solution
x2 + y2 - 50 = 0
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
A circle with its center at the origin, passes through the point (7, 5). Determine the equation of the line that is tangent to this point. Reduce fully.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The tangent is the negative reciprocal of the radius at the point (7, 5). The slope of the tangent is
The slope of the tangent, the negative reciprocal is,
Calculate the b-value, by plugging in the point...
So the equation is,
Circle Word Problems
Pollini's is a famous pizza restaurant located in a major city that delivers within a 12km radius from the restaurant location. A hungry group of business people wants to order from this restaurant and they are located 8km west and 6km south of the restaurant. Will the restaurant deliver to these people?
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Set the pizza place at the origin (0, 0) of a Cartesian plane, the 8km west and 6km south would be (-8, -6)... Determine the hypotenuse (or the radius of the circle)...
The business people are located 10 km away from the restaurant, therefore yes, the restaurant will deliver them.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Set the pizza place at the origin (0, 0) of a Cartesian plane, the 8km west and 6km south would be (-8, -6)... Determine the hypotenuse (or the radius of the circle)...
The business people are located 10 km away from the restaurant, therefore yes, the restaurant will deliver them.
Equation of a Circle, Shifted
Given the equation for a circle with a center at (h, k)...
Determine the equation of the circle with a center at (-4, -3) and a radius of .
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Given the equation of the circle, confirm that the points (-3, 11) and (3, 11) lie on endpoints of a chord of the circle.
Solution
Chords:
- Endpoints of the chord are on the perimeter of the circle
- The chord is less than the diameter (otherwise it is the diameter)
Confirm by substituting points into circle equation and checking if left side equals right side.
And again,
Therefore both points form a chord on the circle with center at (0, 4).
- Endpoints of the chord are on the perimeter of the circle
- The chord is less than the diameter (otherwise it is the diameter)
Calculate the area of the triangle formed between the x-intercept points and the maximum point on the circle... given the equation of the circle below.
Solution
(x - 5)2 + (y - 1)2 = 65
A =
Hint
Clear
Info
Incorrect Attempts:
CHECK
units2
Hint Unavailable
See from the equation that the center of the circle is at: (5, 1)
Determine the maximum height at x = 5...
Determine the x-intercepts by setting y = 0...
Calculate the area... with the x-intercepts forming the base and the max height 9.06 as the height...
Determine the maximum height at x = 5... Determine the x-intercepts by setting y = 0... Calculate the area... with the x-intercepts forming the base and the max height 9.06 as the height...
Determine the equation of the tangent to the point (1, 5) on the circle with the equation below. Reduce fully.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Complete the square for x and y in the circle equation...
The slope of the tangent is the negative reciprocal of the slope between the center (-1, 2) and point (1, 5) ...
Calculate b using ⊥m and a point...
The equation of the tangent is
Applications of Circles
Built in the 1400's, the Duomo in Florence, Italy is still the largest masonry dome in the world. The sides of the arched Duomo lie on part of the perimeters of two circles shown below, where the intersection forms the cross section of the dome. Determine the height of the Duomo if the radius of each circle is 43 m and the base diameter of the Duomo is 45 m. Solution
 |

Applications of Circles, Chords, Distance
A volcano in Iceland erupts with center C(10, 14), the ash cloud formed has radius 3 km and can be modeled with the circle equation below. A weather drone plane flies on route y = 0.8x + 9.
 |
Determine if the weather drone will enter the ash cloud. Prove your reasoning by showing your work in your notes.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Determine the point(s) of intersection (POI), if any...
Expand the circle equation and substitute the linear equation into it...
Sub the linear equation y = 0.8x + 9...
Use the quadratic equation, where a = 1.64, b = -28, c = 116...
Since there are 2 POIs then drone flies through the ash cloud...
Expand the circle equation and substitute the linear equation into it... Sub the linear equation y = 0.8x + 9... Use the quadratic equation, where a = 1.64, b = -28, c = 116... Since there are 2 POIs then drone flies through the ash cloud...
The weather drone manufacturers built the drone with a warranty to withstand flying through a maximum of 3km of ash conditions. Determine if the drone should divert its course.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
In other words, find the coordinates of the POIs to calculate the distance.
First find the coordinates by substituting the 'x' values into the equation...
The points are (7.07, 14.66) and (10, 17)
Calculate the distance (the length of the chord)...
The drone would fly 3.75 km through the ash cloud, and therefore should divert its course to remain under warranty.
First find the coordinates by substituting the 'x' values into the equation... The points are (7.07, 14.66) and (10, 17)
Calculate the distance (the length of the chord)... The drone would fly 3.75 km through the ash cloud, and therefore should divert its course to remain under warranty.
Geometric Properties
Line Segments and Centers
Right bisectors are used to determine the centroid of a triangle.
Solution
- Right bisectors are used to determine the circumcenter of a triangle (and circle).
- Altitudes are used to determine the orthocenter of a triangle
- Midpoints through the opposite vertex are used to determine the centroid of a triangle
- Right bisectors are used to determine the circumcenter of a triangle (and circle).
- Altitudes are used to determine the orthocenter of a triangle
- Midpoints through the opposite vertex are used to determine the centroid of a triangle
Orthocenters and circumcenters can be located outside of their triangles, while centroids cannot.
Solution
This is true in obtuse triangles. Orthocenters and circumcenters can be located outside of their triangles. Centroids are never located outside of their triangles.
Centers
State any one relationship between the three: circumcenter, centroid, and orthocenter.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Any one of the following...
- In equilateral triangles, the circumcenter, centroid, and orthocenter all overlap at one point.
- The circumcenter, centroid, and orthocenter are always arranged forming a line.
- The centroid is always located between the circumcenter and orthocenter.
- The centroid-orthocenter distance is always double the centroid-circumcenter distance.
- In equilateral triangles, the circumcenter, centroid, and orthocenter all overlap at one point.
- The circumcenter, centroid, and orthocenter are always arranged forming a line.
- The centroid is always located between the circumcenter and orthocenter.
- The centroid-orthocenter distance is always double the centroid-circumcenter distance.
Equations of Lines
Determine the equation of a line that passes through point C and the midpoint of AB, given the points: A(1, 2) B(3, 4) and C(5, 6).
Solution
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Find the midpoint of AB...
Find the slope between the midpoint (2, 3) and point C(5, 6)...
Determine 'b' using slope and any point on the line...
So the equation is...
Triangles and Distance
Given the following points, determine if triangle ABC is either scalene, equilateral, or isosceles.
Solution
A(-5, 2) B(4, 2) C(2, -5)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Determine the 3 side length distances...
- 3 equal side lengths = equilateral
- 2 equal side lengths = isosceles
- no equal side lengths = scalene
AB...
AC...
BC...
Since none of the side lengths are equal, the triangle is scalene.
- 3 equal side lengths = equilateral
- 2 equal side lengths = isosceles
- no equal side lengths = scalene
Right Bisectors
A right bisector is located at the midpoint on a line, and is perpendicular to the slope of the line. Given the following points, determine the equation of the right bisector of QR.
Solution
P(3, -1) Q(5, 5) R(0, 3)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
A right bisector is at the midpoint, and is perpendicular to the side.
Determine the midpoint of QR...
Determine the ⊥ slope of the side QR...
Determine the equation using ⊥m and the midpoint on the line...
The equation of the right bisector of QR is...
Determine the midpoint of QR... Determine the ⊥ slope of the side QR... Determine the equation using ⊥m and the midpoint on the line... The equation of the right bisector of QR is...
Circumcenter of a Triangle
Given the following points, determine the circumcenter of the triangle. (Hint: a circumcenter is where all the right bisectors intersect.)
L(2, 2) M(1, 1) N(0, -3)Determine the equation of the right bisector of LM.
Solution
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
With a quick sketch you will see that this triangle is obtuse rather than acute... An you will remember that with obtuse triangles, the circumcenter is located outside of it...
Circumcenters are right bisectors... Find the midpoint...
Find the ⊥m of LM...
Equation of right bisector of LM...
Circumcenters are right bisectors... Find the midpoint... Find the ⊥m of LM... Equation of right bisector of LM...
Determine the equation of the right bisector of MN.
Solution
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
With a quick sketch you will see that this triangle is obtuse rather than acute... An you will remember that with obtuse triangles, the circumcenter is located outside of it...
Circumcenters are right bisectors... Find the midpoint...
Find the ⊥m of MN...
Equation of right bisector of MN...
Circumcenters are right bisectors... Find the midpoint... Find the ⊥m of MN... Equation of right bisector of MN...
Determine the coordinate of the circumcenter. Reduce fully.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The circumcenter is the point of intersection, POI... Find the point of intersection of the right bisectors of LM and MN...
Substitute ① in ②
Determine y...
Therefore the circumcenter is located at
Circumcenters in Circles
A large firestation is to be constructed to service three small municipalities nearby. The city councils require that each city center of each municipality is the exact same distance to the firestation. The city centers are located at...
A (5, 9)B (-10, -9)
C (15, -10)
Determine the coordinate, location where the firestation should be built. Reduce fully.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Place each point on the perimeter of the circle surrounding the firesation at the center. Determine the centroid with the intersection of any 2 medians (using midpoints) from the sides of the triangle...
Midpoint 1... AB:
Midpoint 2... AC:
Slope from MidpointAB to C
Slope from MidpointAC to B
Equation of 1... using mAB & C
Equation of 2... using mAC & C
POI of 1 and 2... (use substitution or elimination)
The firestation should be built at:
Midpoint 1... AB: Midpoint 2... AC: Slope from MidpointAB to C Slope from MidpointAC to B Equation of 1... using mAB & C Equation of 2... using mAC & C POI of 1 and 2... (use substitution or elimination) The firestation should be built at:
Determine the equation of the circle that can be drawn through the city centers around the firestation.
Determine the circumcenter using the midpoints, then get the radius using the distance from a vertex coordinate to the circumcenter coordinate.
Sub into the equation for h, k, and r...
Quadratic Relations
Parabolas: a Simple Sketch First
Sketch the parabola for the following...
Given the table of values for the equation, y = x2 - 4x + 4
| x | y |
| -2 | 16 |
| -1 | 9 |
| 0 | 4 |
| 1 | 1 |
| 2 | 0 |
| 3 | 1 |
| 4 | 4 |
| 5 | 9 |
| 6 | 16 |
Given just the equation,
y = -3x2 + 2
Hint, make your own table of values...
x y = -3(x)2 + 2
bbb ccc
bbb ccc
bbb ccc
bbb ccc
And then sketch...
| x | y = -3(x)2 + 2 |
| bbb | ccc |
| bbb | ccc |
| bbb | ccc |
| bbb | ccc |
Degree of Expressions with one Variable
Determine the degree of each of the following expressions.
4x2 + 3x - 1
Solution
The degree of a polynomial is the magnitude of the highest exponent (or power) term.
3x(2x - 7)(2x + 1)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The highest degree of x will come from
Degree = 3
(7 - 2x2)(3x - 2x3)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The degree will come from the product of the highest terms from the expansion...
Degree = 5
Degree of Expressions with More Than one Variable
Determine the degree of each of the following expressions.
The degree of the following term is 2.
Solution
4x2y1 + x
The degree is the highest sum of all the exponents on variable(s) in one term. The degree of 4x2y1 is 3.
3x3y2z + 2ab2
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The highest sum of exponents is in the term, 3x3y2z. The sum of the exponents is 3 + 2 + 1 = 6. (Don't forget the exponent on z).
So the degree of the expression = 6
So the degree of the expression = 6
(2xy2 - 2x)(3y - 4xy)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The term with the highest sum of exponents comes from the two terms with the highest sum of exponents.
Degree = 5
Degree of Expressions, with Extended Types
Determine the degree of each of the following expressions.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Degree = -2
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Remember the degree is the highest sum of the exponents of variables in one term. The highest is -2 (and not -3).
Degree = -6
Degree = -6
x-2y-1 + x-1y-1
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Remember the degree is the highest sum of the exponents of variables in one term. The highest is -2 (and not -3).
Degree = -2
Degree = -2
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Degree = ½
Functions: Vertical Line Test
A function cannot have:
Solution
Functions: Vertical Line Test: Coordinate Pair Sets
Determine if the following sets are functions:
(-2, 4) (-1, 3) (4, 2) (5, 2)
Solution
Yes this is a function because there are no same values of 'x' with two different values of 'y'.
(-2, 3) (-2, 3) (-1, 7) (2, 3) (5, 4)
Solution
Yes this is still a function because
(-2, 3) and (-2, 3) are the same point and do not count as 2 different y-values for the same x-value
(-2, 3) and (-2, 3) are the same point and do not count as 2 different y-values for the same x-value
(-2, 5) (1, 3) (1, 5) (4, 1) (5, 2)
Solution
No this is not a function because the two points,
(1, 3) and (1, 5)
have 2 different y-values: 3 & 5 for the same x-value: 1
Solve for a point on a function given the x-value
Solve:
when
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
when
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
when
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Review of the Basics: Product Rule
Write each with a single, positive exponent, showing your work without using a calculator.
xa × xb = xa + b
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= 37
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= 52 + (-2)
= 50
= 1
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
= 50
= 1
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= (-10)-5 + 7
= (-10)2
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
= (-10)2
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Review of the Basics: Quotient Rule
Simplify, showing your work without using a calculator.
xa ÷ xb = xa - b
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= 77 - 3
= 74
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
= 74
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= (-2)-11
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= (-5)6 - (-4)
= (-5)10
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
= (-5)10
Exponents: Power of a Power
Write each with a single, positive exponent, or a reduced fraction, showing your work without using a calculator.
(xa)b = xa × b
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= 32 × 4
= 38
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
= 38
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= 22 × 3
= 26
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
= 26
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
22 × 3 × 2
= 212
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
= 212
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Exponents: Negative Powers
Simplify fully to an integer or fraction using positive exponents, showing your work without using a calculator.
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Negative Exponents
Which of the following is the same as: 3-x
Solution
The exponent becomes positive when you flip (make the reciprocal).
Exponent Law Basics
Solution
Exponents: Combinations
Write each with a single, positive exponent, or a reduced fraction, showing your work without using a calculator.
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= 24 - (-2) + (-3)
= 24 + 2 - 3
= 23
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
= 24 + 2 - 3
= 23
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Exponents: Combinations
Simplify as much as possible :
Solution
46
= (4)6
= (22)6
= 212
(As you can see (4)6 is not incorrect, but can be simplified further when 4 is replaced with 22. You will see simplifying the base fully becomes more useful later).
= (4)6
= (22)6
= 212
(As you can see (4)6 is not incorrect, but can be simplified further when 4 is replaced with 22. You will see simplifying the base fully becomes more useful later).
Exponents: Combinations
Write with a single, positive exponent, showing your work without using a calculator.
Solution
Hint
Clear
Info
━━━
Incorrect Attempts:
CHECK
Hint Unavailable
Number Sense: Exponent Rules with Variables: Power Rule with Coefficients
The following simplification of exponents is correct.
Solution
True. This is called the power rule.
Number Sense: Exponent Rules with Variables, Including Negative Exponents
Simplify, answers should have positive exponents only.
Solution
Hint
Clear
Info
━━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
— ━━━
Incorrect Attempts:
CHECK
Hint Unavailable
Exponential Equations
Solve the following exponential equations, similar to the steps shown in the example below. Simplify fully.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Axis of Symmetry Given the Roots
The graph of a quadratic function passes through the ordered pairs (-2, 5) and (8, 5). Determine the equation of the axis of symmetry.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The axis of symmetry is located at the midpoint between two x-values: (think of the midpoint like an average).
The equation is in the form: x = 3
What's The Vertex?
Which of the following equations has a vertex located at the point V(-2, 5)?
Solution
The function with an x-value at x = -2, and a y-value at y = 5 is:
ƒ(x) = -7(x + 2)2 + 5
(remember to switch the sign in the brackets, so +2 becomes -2).
ƒ(x) = -7(x + 2)2 + 5
(remember to switch the sign in the brackets, so +2 becomes -2).
Axis of Symmetry Given the Equation in Vertex Form
Determine the equation of the axis of symmetry given the function,
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Remember to switch the sign in the brackets, so -2 becomes +2
The equation must be written in the form x = 2
The equation must be written in the form x = 2
Basic Elements of Quadratic Functions
The table below shows the flight path of a ball, with distance and height in meters.
| Distance (x) | Height (y) |
| 0 | 1 |
| 1 | 8 |
| 2 | 13 |
| 3 | 16 |
| 4 | 17 |
| 5 | 16 |
| 6 | 13 |
| 7 | 8 |
| 8 | 1 |
Find the vertex
Solution
Hint
Clear
Info
( , )
Incorrect Attempts:
CHECK
Hint Unavailable
Remember back to the optimization you learned last year. The vertex is located at the maximum or minimum of the y-values. In this table, there is a maximum located at (4, 17).
Determine the equation of the axis of symmetry
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The equation of the axis of symmetry is located at the x-value of the maximum point, which is:
x = 4
x = 4
Find the maximum height
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
The maximum height is the highest y-value, which is 17.
Don't forget to write the units:
Therefore the maximum height occurs at 17m.
Don't forget to write the units:
Therefore the maximum height occurs at 17m.
Verify that the equation h = -x2 + 8x + 1 can be used to model the flight path of the ball. [1]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
You verify an equation by substituting 2 or more points into the equation and check that L.S. equals R.S.
Yes, the equation can be used to model the flight path of the ball.
Finite Differences (First and Second)
Use finite differences to determine if the following relations are linear, quadratic, or neither.
Solution
| x | y |
| 0 | 4 |
| 1 | 6 |
| 2 | 8 |
| 3 | 10 |
| 4 | 12 |
6 - 8 = -2
8 - 10 = -2
10 - 12 = -2
All first differences are the same, therefore the relation is linear.
Solution
| x | y |
| 0 | -19 |
| 1 | -12 |
| 2 | -7 |
| 3 | -4 |
| 4 | -3 |
-12 - (-7) = -5
-7 - (-4) = -3
-4 - (-3) = -1
The first differences are not the same, therefore not linear. Find second differences: -7 - (-5) = -2
-5 - (-3) = -2
-3 - (-1) = -2
Since the second differences are the same, then the relation is quadratic.
| x | y |
| 1 | 0 |
| 3 | 1 |
| 5 | 8 |
| 7 | 27 |
| 9 | 64 |
1 - 8 = -7
8 - 27 = -19
27 - 64 = -37
Quadratic Functions
A basketball shot is taken from a horizontal distance of 5 m from the hoop. The height of the ball can be modeled by the equation below. Where h is height in meters, and t is time in seconds since the ball was released.
From what height was the ball first released?
Solution
Video
h =
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
The ball was first released when t = 0 s.
If the ball reached the hoop at 1.0 s, what was the height of the hoop?
Solution
Video
h =
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
Determine the height h(t) when t = 1 s.
What was the maximum height reached by the ball?
Solution
Video
h =
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
Use the formula for the axis of symmetry at the vertex...
a = -7.3, b = 8.25, c = 2.1
The y-value in the vertex (0.57, 4.43) gives us the maximum height.
Therefore the maximum height is 4.43 m.
Therefore the maximum height is 4.43 m.
Given the ball is 4m above the ground at 0.32 seconds, determine the other time when it is at 4m.
Solution
t =
Hint
Clear
Info
Incorrect Attempts:
CHECK
s
Hint Unavailable
Solve using symmetry. Given the point (0.32, 4) and the vertex (0.57, 3.05) you can find the next time.
This is symmetrical with the other side... add 0.25 to the 0.57
The other point is (0.82, 4)
Translations and Vertex Form
Given the general, vertex form of a quadratic.
Which of the following values determines a vertical compression by a certain factor?
Solution
Vertical compression when: 0 < |a| < 1.
Vertical stretch when: |a| > 1.
Vertical compression when: 0 < |a| < 1.
Vertical stretch when: |a| > 1.
Which of the following values determines a reflection in the x-axis?
Solution
Reflection on x-axis when: a < 0... when 'a' is negative.
Parabola opens up when z > 0... when 'a' is positive.
Reflection on x-axis when: a < 0... when 'a' is negative. Parabola opens up when z > 0... when 'a' is positive.
Which of the following values determines the horizontal shift left or right?
Solution
Careful, this is the tricky one!
+h = shift right
-h = shift left
+h = shift right -h = shift left
Transformations of Quadratic Functions
Match the type of transformations - shown with equations - to their respective graphs.
Solution



 Vertical stretch or compression by a factor of 'a'...
Horizontal shift/translation by 'h' units left or right...
Vertical reflection...
Vertical shift/translation by 'k' units up or down...
Vertical stretch or compression by a factor of 'a'...
Horizontal shift/translation by 'h' units left or right...
Vertical reflection...
Vertical shift/translation by 'k' units up or down...




Transformations of Quadratic Functions
State the transformations on the following quadratic functions compared to the parent function, .
Solution
- Vertical compression by a factor of ¼
- Vertical compression by a factor of ¼
Solution
- Vertical translation (shift) up 8 units
- Vertical translation (shift) up 8 units
Solution
- Reflection across the x-axis
- Vertical stretch by a factor of 3
- Reflection across the x-axis
- Vertical stretch by a factor of 3
Solution
Video
- Reflection across the x-axis
- Horizontal translation (shift) 9 units right
- Vertical translation (shift) 1 unit up
- Reflection across the x-axis
- Horizontal translation (shift) 9 units right
- Vertical translation (shift) 1 unit up
Solution
- Reflection across the x-axis
- Horizontal translation (shift) 1 unit left
- Vertical translation (shift) 3 units down
- Reflection across the x-axis
- Horizontal translation (shift) 1 unit left
- Vertical translation (shift) 3 units down
Solution
Video
- Vertical stretch by a factor of 2
- Horizontal compression by a factor of ⅓
- Vertical stretch by a factor of 2
- Horizontal compression by a factor of ⅓
Solution
Video
- Horizontal translation (shift) 2 units right
- Vertical translation (shift) 4 units up
- Horizontal translation (shift) 2 units right
- Vertical translation (shift) 4 units up
Solution
Video
- Reflection across the x-axis -ƒ(x)
- Reflection across the y-axis ƒ(-x)
- Reflection across the x-axis -ƒ(x)
- Reflection across the y-axis ƒ(-x)
Transformations of Quadratic Functions
Given the general form of a quadratic, determine the equation of a quadratic function with the transformations listed below....
Reflection in the x-axis, vertical stretch by a factor of 3, vertical translation 5 units up.
Solution
A parabola with vertex at (-1, 3), opening upward, and with a vertical compression by a factor of ⅛.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Transformations of a Point Quadratic Functions
Transform the point (1, 2) according to the same transformations in the function below. The point (1, 2) transforms into which of the following?
Solution
y = -2(x + 1)2 - 3
Hint
Clear
Info
( , )
Incorrect Attempts:
CHECK
Hint Unavailable
y = -2(x + 1)2 - 3
Reflection in the x-axis. ← Affects y
Vertical stretch by a factor of 2. ← Affects y
Translation 1 unit left. ← Affects x
Translation 1 unit down. ← Affects y
Reflection in the x-axis. ← Affects y
Vertical stretch by a factor of 2. ← Affects y
Translation 1 unit left. ← Affects x
Translation 1 unit down. ← Affects y
Two Other Transformations of Quadratic Functions
Based on the value 'n' determine some of the horizontal transformations below.
The transformation to y = a[n(x - h)]2 + k with a horizontal reflection.
Solution
A horizontal reflection is due to ƒ(-x), or in an other form, y = a[-n(x - h)]2 + k.
For example consider the transformation of to .
For example consider the transformation of to .
The transformation to y = a[n(x - h)]2 + k with a horizontal stretch by a factor of 5. (careful here)
Solution
The vertical stretch or compression is by a factor of !
So for a horizontal stretch by a factor of 5, the 'n' value must be ⅕ ... because .
So for a horizontal stretch by a factor of 5, the 'n' value must be ⅕ ... because .
Sketching Graphs of Functions
Sketch the graphs of the following functions. Label the x-intercepts, the axis of symmetry, and the vertex for each.
Solution
x-intercepts: x = -2, +2
Equation of axis of symmetry: x = 0
Vertex: sub the axis of symmetry (x = 0) into function:
Vertex: (0, -4)
Equation of axis of symmetry: x = 0
Vertex: sub the axis of symmetry (x = 0) into function: Vertex: (0, -4)
Solving X-Intercepts with Symmetry
The vertex of a parabola is (-3, 4). The x-intercepts are located at: -8 and +8.
Solution
The x-intercepts must have the same ∆x distance to the axis of symmetry (x = -3).
-8 → -3 = +5
-3 → +8 = +11...
-8 → -3 = +5
-3 → +8 = +11...
Solving for Quadratic Equations Given Certain Properties
Find an equation for the parabola with vertex (-3,4) and a y-intercept of 1.
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Given
Vertex: (-3, 4)
h = -3
k = 4
Point: (0, 1)
x = 0
y = 1
Vertex: (-3, 4)
h = -3
k = 4
Point: (0, 1)
x = 0
y = 1
Using the Discriminant
The following table contains the correct number of x-intercepts for each outcome of the discriminant equation. Solution Video
| Number of x-intercepts | b2 - 4ac |
| 0 | Negative |
| 1 | Zero |
| 2 | Positive |
Discriminant equals zero (b2 - 4ac) = 0 means: 1 x-intercept
Positive discriminant (b2 - 4ac) > 0 means: 2 x-intercepts
The following function has two real roots.
Solution
A function has 2 real roots when (b2 - 4ac) > 0
It is possible for a function to have two equal, real roots.
Solution
True. The following is considered to have 2 equal (real) roots:
y = (x + 2)2
The Three Ways to Find a Vertex
Find the vertex using each of the following methods:

By completing the square:
Solution
Hint
Clear
Info
( , )
Incorrect Attempts:
CHECK
Hint Unavailable
Vertex: (-3, -28)
Using the formula for the x-value of the vertex:
Solution
Hint
Clear
Info
( , )
Incorrect Attempts:
CHECK
Hint Unavailable
a = -4.5, b = -1.8, c = 3.
Vertex: (-0.2, 3.18)
Solve using symmetry:
Solution
Hint
Clear
Info
( , )
Incorrect Attempts:
CHECK
Hint Unavailable
Roots at x = 1, -5.
Axis of symmetry at x = -2
Vertex: (-2, -18)
Axis of symmetry at x = -2 Vertex: (-2, -18)
Solving Quadratic Functions
A soccer ball is kicked upward on the field. The height, ‘h’, of the ball in meters is given by the function below, where ‘t’ is the time in seconds. Find the maximum height and the time the ball reaches its maximum height.
Solution
Hint
Clear
Info
Height = m
Time = s
Incorrect Attempts:
CHECK
Hint Unavailable
The maximum height occurs at the y-value of the vertex.
Solve by completing the square:
Vertex: (1, 10)
The maximum height is 10 m at a time of 1s.
Time = s
Solve by completing the square: Vertex: (1, 10)
The maximum height is 10 m at a time of 1s.
Solving Quadratic Functions
Given the x-intercepts of a function are -1 and 3, and the y-intercept is 6, the equation of the parabola is
Solution
Put the x-intercepts into the general form of the quadratic in standard form...
The y-intercept (6) occurs where x = 0 ...
ƒ(0) = 6 ...
So putting this together we get,
ƒ(0) = 6 ... So putting this together we get,
Solving Using Symmetry in the Quadratic Relations Unit
A parabola has vertex (-3, 7), and one x-intercept is -11. Find the other x-intercept and the y-intercept (reduce fully).
Solution
Hint
Clear
Info
x-intercept:
( , )
y-intercept:━━━
Incorrect Attempts:
CHECK
Hint Unavailable
First find the other x-intercept with symmetry.
x = +5
The x-intercept is at (5, 0)
To find the y-intercept, determine the equation first... plug in the points (-3, 7) and (-11, 0)
Then set x = 0...
y-intercept:━━━
x = +5
The x-intercept is at (5, 0) To find the y-intercept, determine the equation first... plug in the points (-3, 7) and (-11, 0) Then set x = 0...
Solving Using Quadratic Relations, and Vertex Form
A quadratic function passes through the points (-1, 1), (0, -3), and (5, 1).
Determine the equation in standard form.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
You want to solve the system of equations. First substitute the easiest point which has a zero in it, (0, -3) the y-intercept into standard form...
Substitute 'c' and the point (-1, 1) in...
Substitute 'c' and the point (5, 1) in...
Substitute b = a - 4 into the other equation to solve for 'a' and 'b'...
Solve for 'b'...
So the equation is,
Determine the equation in vertex form.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
First determine the Axis of Symmetry (AOS) of the quadratic. The AOS goes through the vertex and is the midpoint of two points on the same horizontal line: (-1, 1) and (5, 1).
Substitute AOS and the easiest point (0, -3) into the vertex form... This AOS represents 'h' in the equation...
Substitute AOS and any other point, (-1, 1)...
Solve with elimination...
Now find the last value, 'k by subbing in the last point (5, 1)...
Here is your equation in vertex form,
Quadratic Expressions
| Specific Topic | General Topic | School | Date |
|---|---|---|---|
| The Correct Way to Expand a Squared Binomial | Expanding | Branksome | Sep 2013 |
| Factoring a Perfect Square Trinomial | Quadratics | Branksome | Sep 2013 |
| Factoring Unordered Trinomials Example 1 | Quadratics | Branksome | Sep 2013 |
| Factoring Unordered Trinomials Example 2 | Quadratics | Branksome | Sep 2013 |
Review of Basics
Simplify by collecting like terms.
(2x2 – 3x + 1) – (–x2 – 3x – 5)
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
Distribute the negative and remove parentheses, then collect like terms.
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
(5x2 – y) + (6y – 2x2) – (y2 + 7x2)
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
Distribute the negative and remove parentheses, then collect like terms.
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Terminology
What is the difference between an expression and an equation?
Solution
An equation consists of 2 or more terms, including an equal sign.
An expression is just 1 or more term(s).
An expression is just 1 or more term(s).
Care with Distributive Property of Terms
Find the term that has the mistake in the following statement.
Solution
3x(2x - 3) = 6x - 9x
6x is wrong because is an incorrect use of the distributive property. It should be 6x2.
3x(2x - 3) = 6x2 - 9x
3x(2x - 3) = 6x2 - 9x
FOIL
What does FOIL stand for?
Solution
When you expand two binomials like (x + 3)(4x - 1), FOIL is the order that you multiply the numbers in...
FOIL (A + B)(C + D) = AC + AD + BC + BD
Expand and simplify. Write in standard form.
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
FOIL first:
Then distribute the negative sign into each term in parenthesis:
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
! Careful, do not do this:
FOIL first, then collect like terms:
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
FOIL first, then collect like terms:
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
FOIL first, then collect like terms.
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Expanding Using FOIL
Determine the expanded standard form of (2x - 3)(4x + 1), hence FOIL.
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
FOIL and put your answer in standard form
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Expanding using FOIL is the reverse of factoring (and factoring is the reverse of FOIL).
FOIL with roots
Expand and simplify.
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
FOIL and put your answer in standard form
FOIL first, then collect like terms.
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Factoring Quadratic Expressions, Common Factoring
The greatest common factor (GCF) is used to common factor an expression. Determine the GCF of the following.
Solution
Video
16x2y + 8xy + 12y2
Hint
Clear
Info
Incorrect Attempts:
CHECK
Determine the GCF of the coefficients and the variables.
4 is the greatest factor of the numbers 16, 8, and 12.
The highest degree of the common exponent is y1, or just y.
GCF = 4y
The highest degree of the common exponent is y1, or just y. GCF = 4y
Factoring Quadratic Expressions, Common Factoring
Factor.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The highest number you can factor out is 5.
It doesn't matter if it's xy or yx...
The highest degree of x that can be common factored is x1.
The highest degree of y that can be common factored is y1.
Shown in steps:
It doesn't matter if it's xy or yx...
The highest degree of x that can be common factored is x1.
The highest degree of y that can be common factored is y1.
Shown in steps:
Factor by Grouping
Factor the following, with the grouping already done for you. (Grouping step is an optional intermediate step).
Solution
2x(3x - 1) - 2(3x - 1)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
This shows the step midway through factoring by grouping:
2x(3x - 1) - 2(3x - 1)
= (2x - 2)(3x - 1)
2x(3x - 1) - 2(3x - 1)
= (2x - 2)(3x - 1)
Factoring Quadratic Expressions, Trinomials when a = 1
Factor, using any method.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
For factoring quadratics where there's nothing but 1 in-front of the x2...
The numbers that multiply to 12:
1 × 12, 2 × 6, 3 × 4
Choose the pair that adds to 7... 3 × 4
= (x + 3)(x + 4)
Or you could do factor by grouping:
The numbers that multiply to 12:
1 × 12, 2 × 6, 3 × 4
Choose the pair that adds to 7... 3 × 4
= (x + 3)(x + 4)
Or you could do factor by grouping:
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The numbers that multiply to -20:
-1 × 20, 1 × -20, -2 × 10, 2 × -10, -4 × 5, 4 × -5
The pair that adds to +19: -1 × 20
= (x - 1)(x + 20)
Or you could do factor by grouping:
-1 × 20, 1 × -20, -2 × 10, 2 × -10, -4 × 5, 4 × -5
The pair that adds to +19: -1 × 20
= (x - 1)(x + 20)
Or you could do factor by grouping:
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The numbers that multiply to -24:
-1 × 24, 1 × -24, -2 × 12, 2 × -12, -3 × 8, 3 × -8, -4 × 6, 4 × 6
= (x + 3)(x - 8)
Or you could do factor by grouping:
-1 × 24, 1 × -24, -2 × 12, 2 × -12, -3 × 8, 3 × -8, -4 × 6, 4 × 6
= (x + 3)(x - 8)
Or you could do factor by grouping:
Factoring Quadratic Expressions, Factor by Grouping to Prepare for Trinomials with a ≠ 1
Before factoring a trinomial in the form ax2 + bx + c, where a ≠ 1, it is best to try to common factor first.
Solution
Common factoring first will make factoring easier when you have to think:
- what two numbers multiply to make...
- and what two number add to make...
- what two numbers multiply to make...
- and what two number add to make...
Factoring Quadratic Expressions, Factor by Grouping to Prepare for Trinomials with a ≠ 1
Factor by grouping, or by using the direct method.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The first and last pairs are already common factored for you.
= 3x(x - 2) + 5(x - 2)
= (3x + 5)(x - 2)
= 3x(x - 2) + 5(x - 2)
= (3x + 5)(x - 2)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The middle term is already split for you. Next (group) common factor the first pair, and then the last pair.
= x2 + 2x + 4x + 8
= x(x + 2) + 4(x + 2)
= (x + 2)(x + 4)
= x2 + 2x + 4x + 8
= x(x + 2) + 4(x + 2)
= (x + 2)(x + 4)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The middle term is already split for you. Next (group) common factor the first pair, and then the last pair.
= x2 + 2x - 6x - 12
= x(x + 2) - 6(x + 2)
= (x - 6)(x + 2)
= x2 + 2x - 6x - 12
= x(x + 2) - 6(x + 2)
= (x - 6)(x + 2)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The middle term is already split for you. Next (group) common factor the first pair, and then the last pair.
= 6x2 + 2x + 15x + 5
= 2x(3x + 1) + 5(3x + 1)
= (2x + 5)(3x + 1)
= 6x2 + 2x + 15x + 5
= 2x(3x + 1) + 5(3x + 1)
= (2x + 5)(3x + 1)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Think of two numbers that add to -12, and multiply to -28, from (7)(-4).
Strategy: write the factors of 28: 1 × 28, 2 × 14, 4 × 7.
The numbers are: -14, and 2.
= 7x2 - 14x + 2x - 4
= 7x(x - 2) + 2(x - 2)
= (x - 2)(7x + 2)
Strategy: write the factors of 28: 1 × 28, 2 × 14, 4 × 7.
The numbers are: -14, and 2.
= 7x2 - 14x + 2x - 4
= 7x(x - 2) + 2(x - 2)
= (x - 2)(7x + 2)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Think of two numbers that add to +2, and multiply to -120, from (8)(-15).
The numbers are: +12, and -10.
= 8x2 + 2x - 15
= 8x2 + 12x - 10x - 15
= 4x(2x + 3) - 5(2x + 3)
= (2x + 3)(4x - 5)
The numbers are: +12, and -10.
= 8x2 + 2x - 15
= 8x2 + 12x - 10x - 15
= 4x(2x + 3) - 5(2x + 3)
= (2x + 3)(4x - 5)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
As with the rest of the questions here, you can factor by grouping (common factor the first and last pairs). Basically apply what you already know (common factoring).
= 3x2 - x + 6xy - 2y
= x(3x - 1) + 2y(3x - 1)
= (x + 2y)(3x - 1)
= 3x2 - x + 6xy - 2y
= x(3x - 1) + 2y(3x - 1)
= (x + 2y)(3x - 1)
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
Think of two numbers that add to +2, and multiply to -120, from (8)(-15).
The numbers are: +12, and -10.
= 8x4 + 2x2 - 15
= 8x4 + 12x2 - 10x2 - 15
= 4x2(2x2 + 3) - 5(2x2 + 3)
= (2x2 + 3)(4x2 - 5)
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
The numbers are: +12, and -10.
= 8x4 + 2x2 - 15
= 8x4 + 12x2 - 10x2 - 15
= 4x2(2x2 + 3) - 5(2x2 + 3)
= (2x2 + 3)(4x2 - 5)
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
Think of two numbers that add to -5...
= 6x4 - 8x2 + 3x2 - 4
= 2x2(3x2 - 4) + 1(3x2 - 4)
= (2x2 + 1)(3x2 - 4)
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
= 6x4 - 8x2 + 3x2 - 4
= 2x2(3x2 - 4) + 1(3x2 - 4)
= (2x2 + 1)(3x2 - 4)
Factoring Quadratic Expressions, Factor by Grouping to Prepare for Trinomials with a ≠ 1
Factor the following
Solution
3x2 + 2x - 8
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Which of the following is factored correctly?
Solution
-30x2 + 130x + 100
Common factor the greatest common multiple first...
Factoring Quadratic Expressions, Trinomials when a ≠ 1
Factor by decomposition (splitting & grouping), or directly if you are able. Remember to factor fully (with any common factors).
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Two numbers that multiply to +6, from (2 × 3) and add to +7 are:
+1 & +6


Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(x - 2)(5x + 3)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(2x + 1)(3x - 4)
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Two numbers that add to +4 and multiply to -60... -6 & +10...
It is good form to common factor first actually, although common factoring at the end is acceptable.
Best to common factor first. What two numbers add to +2 and multiply to -15... +5 & -3...
Best to common factor first. What two numbers add to +2 and multiply to -15... +5 & -3...
Faster Factoring Without Decomposition
Now that you understand more about factoring it's time to take the training wheels off - no more decomposition (aka splitting and grouping). Factor straight into the parenthesis like the example shown below.
What multiplies to +18 and adds to +11? = +9 and +2x2 - 11x + 18
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
What multiplies to +18 and adds to -11?
= -9, -2...
= -9, -2...
3x2 - 7x - 6
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
What multiplies to -18 and adds to -7?
= -9, +2...
= -9, +2...
9x2 + 7x - 2
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
What multiplies to -18 and adds to +7?
= +9, -2...
= +9, -2...
8x2 + 2x - 3
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
-10x2 - 22x - 4
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Common factor out the negative first, and common factor the
It is considered better form to factor the 2 out,
Factoring Quadratic Expressions, Perfect Squares
Factor the following perfect squares fully, using any method (direct is encouraged). The general formulas for perfect squares are given below.
x2 + 2x + 1
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
(x + 1)2
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
x2 + 10x + 25
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
(x + 5)2
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
x2 - 8x + 16
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
(x - 4)2
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
x2 - 20x + 100
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
(x - 10)2
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
4x2 - 12x + 9
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
(2x - 3)2 or (3 - 2x)2
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Quadratic Expressions That Are Not Factorable
Explain in your own words why the following two examples of quadratics are not factorable.
Solution
y = x2 + 6x + 12
y = x2 - 3x + 10
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
They are not factorable when no two numbers add to the middle term and multiply to the product of the first and last terms.
(Also accept a more in-depth exploration of this).
(Also accept a more in-depth exploration of this).
Factoring Quadratic Expressions, Perfect Squares
Given the general formula for a perfect square quadratic...
E.g. 1) (a)2x2 + 2(a)(b)x + (b)2= (ax + b)2 E.g. 2) x2 + 6x + 9
= (a)2x2 + 2(a)(b)x + (b)2
= (1)2x2 + 2(1)(3)x + (3)2
= (1x + 3)2
Determine the value of n that would make the following trinomial a perfect square.
Solution
9x2 + nx + 16
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Find the value of n that would make the following trinomial a perfect square, and then write it as a perfect square.
Solution
25x2 + 30x + n2
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
See that 30x = 2(5)(n)x and solve...
Types of Polynomials
The following expression is a difference of squares.
Solution
(2x - 1)2
This is actually a perfect square: (2x - 1)2
A difference of squares is in the form a2 - b2 = (a + b)(a - b)
A difference of squares is in the form a2 - b2 = (a + b)(a - b)
Factoring Quadratic Expressions, Difference of Squares: a2 - b2 = (a + b)(a - b)
Factor the difference of squares fully (meaning common factor whenever possible). Show as much work in your notes as you need.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(x + 5)(x - 5)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
= 9(x2 - 16)
= 9(x - 4)(x + 4)
(Best form to common factor as much as possible out... often get -0.5 mark taken off if not done.)
= 9(x - 4)(x + 4)
(Best form to common factor as much as possible out... often get -0.5 mark taken off if not done.)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
= 4(4x2 - 25y2)
= 4(2x - 5y)(2x + 5y)
(Best form to common factor as much as possible out... often get -0.5 mark taken off if not done.)
= 4(2x - 5y)(2x + 5y)
(Best form to common factor as much as possible out... often get -0.5 mark taken off if not done.)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Factor in the form...
= 4(9 - y2)
= 4(3 + y)(3 - y)
or = -4(y - 3)(y + 3)
= 4(3 + y)(3 - y)
or = -4(y - 3)(y + 3)
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= (x2)2 - (3)2
= (x2 + 3)(x2 - 3)
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
= (x2 + 3)(x2 - 3)
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= (5x + 6n2)(5x - 6n2)
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= (x4)2 - (9)2
= (x4 + 9)(x4 - 9)
= (x4 + 9)[(x2)2 - (3)]
= (x4 + 9)(x2 + 3)(x2 - 3)
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
= (x4 + 9)(x4 - 9)
= (x4 + 9)[(x2)2 - (3)]
= (x4 + 9)(x2 + 3)(x2 - 3)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
= (11)2 - (x + 1)2
= [11 + (x + 1)][11 - (x + 1)]
= (x + 12)(12 - x)
= [11 + (x + 1)][11 - (x + 1)]
= (x + 12)(12 - x)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
You can even factor this like a difference of squares... just using roots in the form...
So,
Tough Quadratic
Factor fully:
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Determine the factor pairs that multiply to +400 and add to -41...
±1 & ±400
±2 & ±200
±4 & ±100
±5 & ±80
±8 & ±50
±10 & ±40
-16 & -25 !
Factor by splitting and grouping (shown here)...
= x4 - 25x2 - 16x2 + 400
= x2(x2 - 25) - 16(x2 - 25)
= (x2 - 16)(x2 - 25) <-- Recognize the difference of squares!
= (x + 4)(x - 4)(x + 5)(x - 5)
-16 & -25 !
Factor by splitting and grouping (shown here)...
= x4 - 25x2 - 16x2 + 400
= x2(x2 - 25) - 16(x2 - 25)
= (x2 - 16)(x2 - 25) <-- Recognize the difference of squares!
= (x + 4)(x - 4)(x + 5)(x - 5)
Types of Polynomials
Which of the following is a perfect square trinomial?
Solution
Perfect squares are in the form: a2 + 2ab + b2, or a2 - 2ab + b2
Algebraic Expressions and Factoring
The dimensions for two rectangles are given below. Determine an expression for the total area of the two rectangles combined, then combine like terms and factor this expression fully. Solution
| Rectangle A | Rectangle B | |
| Length (cm) | (2x - 3) | 4 |
| Width (cm) | 3x | (x - 1) |
Algebraic Expressions and Factoring
A triangular sandbox is surrounded by a rectangular field of grass. The dimensions of the sandbox and field are listed below, in terms of x.
| Base (cm) | Height (cm) | Length (cm) | Width (cm) | |
| Triangle | 2x | x + 4 | ||
| Rectangle | x + 1 | 4x - 4 |
Determine a standard form expression for the area of the grass surrounding the sandbox.
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
Sandbox: x2 + 4x
Field: 4x2 + 0x - 4
Combined Expression: 3x2 - 4x - 4
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Field: 4x2 + 0x - 4
Combined Expression: 3x2 - 4x - 4
Factor the expression fully.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
3x2 - 4x - 4
= 3x2 + 2x - 6x - 4
= x(3x + 2) - 2(3x + 2)
= (3x + 2)(x - 2)
= 3x2 + 2x - 6x - 4
= x(3x + 2) - 2(3x + 2)
= (3x + 2)(x - 2)
Algebraic Expressions and Factoring
The volume of a rectangular prism is represented by the following trinomial. Determine a factored-form expression for the dimensions in terms of x with the length, width, and height.
Solution
Volume = 2x3 + 8x2 + 6x
V =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
V = (l) × (w) × (h)


Algebraic Expressions and Factoring
Determine the most simplified expression for the total surface area of a cube with side lengths equal to (2x - 3).
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
There are 6 equal faces on a cube.
The area of each face is (2x - 3)(2x - 3) = (2x - 3)2
The total surface area = 6(area)
= 6(2x - 3)2
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
The area of each face is (2x - 3)(2x - 3) = (2x - 3)2
The total surface area = 6(area)
= 6(2x - 3)2
Quadratic Equations
| Specific Topic | General Topic | School | Date |
|---|---|---|---|
| Solving for X by Completing the Square | Factoring Quadratics | Branksome | Sep 2013 |
Solving Factored Quadratics Using Zero Product Property
Given the equation already in factored form.
How many solutions will there be?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
solutions
Hint Unavailable
One solution will come from the first, x = 0
The other solution will come from the second, 2x - 3 = 0
Therefore there are 2 solutions.
The other solution will come from the second, 2x - 3 = 0
Therefore there are 2 solutions.
Solve using the zero-product property.
Solution
Hint
Clear
Info
x1 = x2 = ━━
Incorrect Attempts:
CHECK
Hint Unavailable
Remember that if
Then a = 0, or b = 0...
So for,
There are two answers:
So for, There are two answers:
Solutions: Mixed
Determine the solutions, hence solve. Use the zero-product property or complete the square where most applicable. Order solutions from lowest to highest...

y = x2 + 8x + 15
Solution
Video
Hint
Clear
Info
x1 = x2 =
Incorrect Attempts:
CHECK
Hint Unavailable
3 & 5 add to +8 and multiply to +15...
14 = x2 + 5x
Solution
Hint
Clear
Info
x1 = x2 =
Incorrect Attempts:
CHECK
Hint Unavailable
Rearrange the trinomial into standard form first, then factor.
14 = x2 + 5x
0 = x2 + 5x - 14
0 = (x + 7)(x - 2)
x = -7, + 2
14 = x2 + 5x
0 = x2 + 5x - 14
0 = (x + 7)(x - 2)
x = -7, + 2
x2 - 9x = 0
Solution
Video
Hint
Clear
Info
x1 = x2 =
Incorrect Attempts:
CHECK
Hint Unavailable
x2 - 9x = 0
(x)(x - 9) = 0
x = 0, 9
(x)(x - 9) = 0
x = 0, 9
* (6x - 1)2 = 49
Solution
Hint
Clear
Info
x1 = x2 = ━━
Incorrect Attempts:
CHECK
Hint Unavailable
Cannot factor, solve by taking square root of both sides and order of operations...
y = 3x2 - 11x - 20
Solution
Video
Hint
Clear
Info
x1 = ━━x2 =
Incorrect Attempts:
CHECK
Hint Unavailable
Set y equal to zero and factor by splitting and grouping...
What numbers add to -11 and multiply to -20?
1 & 60, 2 & 30, 3 & 20,, 4 & 15...
What numbers add to -11 and multiply to -20?
-2x2 + 5x = -3
Solution
Hint
Clear
Info
x1 = ━━x2 =
Incorrect Attempts:
CHECK
Hint Unavailable
0 = -(2x + 1)(x - 3)
x = -1/2, 3
x = -1/2, 3
x4 - 9x2 = 0
Solution
Hint
Clear
Info
x1 = x2 = x3 =
Incorrect Attempts:
CHECK
Hint Unavailable
This question has two rounds of differences of squares...
x4 - 9x2 = 0
(x2)(x2 - 9) = 0
(x2)(x + 3)(x - 3) = 0
x = 0, -3, +3
x = -3, 0, 3
x4 - 9x2 = 0
(x2)(x2 - 9) = 0
(x2)(x + 3)(x - 3) = 0
x = 0, -3, +3
x = -3, 0, 3
3x2 + 14x = -8
Solution
Hint
Clear
Info
x1 = x2 = ━━
Incorrect Attempts:
CHECK
Hint Unavailable
You can solve by factoring, but
completing the square is shown here...
completing the square is shown here...
2x2 + 4nx - 5n2 in terms of n...
Solution
Since not factorable, solve by completing the square...
Solutions and Vertex
Given the quadratic: y = 4x2 - 36,
Determine the x-intercepts, hence factor.
Solution
Hint
Clear
Info
x1 = x2 =
Incorrect Attempts:
CHECK
Hint Unavailable
The x-intercepts are:
x = -3, +3
x = -3, +3
Determine the vertex, hence show in vertex form.
Solution
Hint
Clear
Info
( , )
Incorrect Attempts:
CHECK
Hint Unavailable
This form is basically already in vertex form,
The vertex is (0, -36).
Algebraic Equations and Factoring
A rectangle has the following dimensions: length = (2x - 5), and width = (4x + 2).
Write an expression for the area of the rectangle, in standard form.
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
If the area of the rectangle equals 14cm2, then find the dimensions of the sides in centimetres.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Notice that this questions is not asking for a "maximum" or "minimum"...
So you are looking for the roots...
To find the dimensions you need to find x-intercepts not x-value of vertex:
So you are looking for the roots...
To find the dimensions you need to find x-intercepts not x-value of vertex:
Determine the Vertex: Complete the Square
Rewrite the equation in vertex form by completing the square.
Solution
Video
y = x2 + 4x + 6
Determine the Vertex: Complete the Square
Rewrite the equation in vertex form by completing the square.
y = x2 - 6x + 8
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
y = 2x2 + 4x + 6
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
y = 4x2 - 8x + 1
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
y = 3x2 + 18x
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The equation of the axis of symmetry is x = -3
y = -2x2 + 6x + 2
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
y = -4x2 + 5x + 1
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
y = ax2 + bx + c
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Determine the Vertex: Complete the Square with Fractions and Decimals
Rewrite the equation in vertex form by completing the square.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Vertex Form
The equation of the axis of symmetry is: x = - 3
Solution
y = -5x2 - 30x + 12
x = -3
The equation of the axis of symmetry is: x = - 3
The equation of the axis of symmetry is: x = - 3
Vertex Form
The minimum occurs at...
Solution
y = -3x2 + 6x - 20
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Determine the minimum 'y' value (of the vertex)
One of the main ways to determine a maximum/minimum is to convert the quadratic equation from standard form to vertex form. The minimum is the y-value of the vertex.
Complete the square:
y = -3x2 + 6x - 20
y = -3(x2 - 2x) - 20
y = -3(x2 - 2x + 1 - 1) - 20
y = -3(x2 - 2x + 1) - 20 + (-3)(-1)
y = -3(x2 - 2x + 1) - 17
y = -3(x - 1)(x - 1) - 17
y = -3(x - 1)2 - 17
Complete the square:
y = -3x2 + 6x - 20
y = -3(x2 - 2x) - 20
y = -3(x2 - 2x + 1 - 1) - 20
y = -3(x2 - 2x + 1) - 20 + (-3)(-1)
y = -3(x2 - 2x + 1) - 17
y = -3(x - 1)(x - 1) - 17
y = -3(x - 1)2 - 17
The maximum point is (1, 20)
Solution
y = 8x2 - 16x + 20
The function opens upwards because +8x2 is postive, therefore the vertex is a minimum point.
Convert Vertex Form to Standard Form
Convert to standard form: y = -3(x - 2)2 + 4
Solution
y =
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
y = -3(x - 2)2 + 4
y = -3(x - 2)(x - 2) + 4
y = -3(x2 - 2x - 2x + 4) + 4
y = -3(x2 - 4x + 4) + 4
y = -3x2 + 12x + -12 + 4
y = -3x2 + 12x - 8
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
y = -3(x - 2)(x - 2) + 4
y = -3(x2 - 2x - 2x + 4) + 4
y = -3(x2 - 4x + 4) + 4
y = -3x2 + 12x + -12 + 4
y = -3x2 + 12x - 8
Maximum and Minimum Word Problems
The trajectory of a dud firecracker launched by astronauts on a planet with oxygen and high gravity is recorded with height in meters and time, t in seconds. What is the maximum height of the firecracker on the planet?
Solution
h(t) = -2t2 + 10t + 1
h =
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
The maximum height is the y-value of the vertex.
The maximum height is 13.5m
Revenue, Expense, and Profit
The revenue, expense, and profit functions are given below, where x is the number of items sold.
Make a profit equation, and factor fully.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Determine the number of items sold at the break even point (when profit equals zero).
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
items
Hint Unavailable
Profit equals zero so substitute '0' into the left hand side of your profit equation:
Solve for x when y = 0 by factoring, rather than completing the square to find vertex.
x cannot be negative (because you can't have a negative number of things sold.)
∴ the break even point occurs when 5 items are sold.
Solve for x when y = 0 by factoring, rather than completing the square to find vertex.
x cannot be negative (because you can't have a negative number of things sold.)
∴ the break even point occurs when 5 items are sold.
Maximum and Minimum Word Problems
The cost of operating a machine, in dollars, is given by the formula below where t is time, in hours, that the machine operates.
C(t) = 2t2 - 16t + 682What is the minimum cost of running the machine
Solution
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The minimum cost is the y-value of the vertex.
The minimum cost is $650
For how many hours must the machine run to reach this minimum cost?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
hours
Hint Unavailable
The hours is the x-value of the vertex.
C(t) = 2(x - 4)2 + 650
The machine runs for 4 hours.
C(t) = 2(x - 4)2 + 650
The machine runs for 4 hours.
Maximum and Minimum Word Problems
A hamburger store can sell 120 hamburgers per week at $4.00 per hamburger. For each $0.50 decrease in price, they can sell 20 more hamburgers.
Determine an algebraic expression in standard form, for the maximum revenue.
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
Let 'x' represent number of times the price changes by $0.50
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
What price should the store charge to maximize revenue?
Solution
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
To solve for price ($4 - $0.50x), you need to find the value of 'x' of the vertex.
You can find the x-value by completing the square: (note that you can also find the x-value of the vertex by symmetry, or the equation x = -b/2a).
You can find the x-value by completing the square: (note that you can also find the x-value of the vertex by symmetry, or the equation x = -b/2a).
Word Problem: Solving for Elements of Quadratic Equations
Given the following elements of a quadratic function, write the equation in factored form. Solution
| Axis of Symmetry: | = -4 |
| x-intercept: | (-6, 0) |
| y-intercept at: | y = 12 |
Root 1: (-6, 0)
Point 2: (0, 12)
Using symmetry, Root 2: (-2, 0)
Word Problem: Solving for Elements of Quadratic Equations
Write an equation, in standard form, to represent a parabola with: Solution
| x-intercepts: | (-4, 0) and (5, 0) |
| vertex: | (1, 40) |
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Root 1: (-4, 0)
Root 2: (5, 0)
Point 3: (1, 40)
Word Problem: Solving for Elements of Quadratic Equations
Write an equation, in vertex form, to represent a parabola that passes through the origin and the points: and Solution
 |
Equation ①: substituting ... Equation ②: substituting ... Equation ③: substituting ... Substitute equation ① into ② and substitute equation ① into ③ to get two equations for h... Now that you have 2 equations and 2 unknowns (h & a) you can use substitution to solve the system.
Set h = h ... hence solve for a... Solve for h... Solve for k... Finally after all that algebra practice! Your equation is...
Quadratic Equations Theory
Explain what must be true for a parabola to have only one x-intercept.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
There will only be one solution for x, one point.
One root means the quadratic equation will turn out to be a perfect square when completing the square...
When setting ƒ(x) = 0, the discriminant will equal zero...
One root means the quadratic equation will turn out to be a perfect square when completing the square...
When setting ƒ(x) = 0, the discriminant will equal zero...
Deriving the Quadratic Formula
Derive the quadratic formula from the general quadratic equation in standard form. Show your work in your own notes.
Solution
ax2 + bx + c = 0
Complete the square with a quadratic in standard form: ax2 + bx + c = 0...


Quadratic Formula
Solve, using a calculator.
Solution
Split into two different based on ±
Quadratic Formula
To solve the trinomial, 2x2 - 7x = -4, which cannot be factored we must use the quadratic equation. The quadratic equation has been used correctly below.
Solution
Quadratic Formula
When using the quadratic formula, what indicates that there are no x-intercepts?
Solution
This is the discriminant (b2 - 4ac). Since it is underneath a square root, a negative value indicates 'no real roots' (no x-intercepts)
Mistakes to Avoid Solving Equations
In the statement below, 'x' equals which of the following values?
Solution
Vertex to Factored Form
The following equation in vertex form represents the size of the opening of the arch of the Basilica of Maxentius and Constantine in Rome. If the side of each arch is located at an x-intercept of the function below, determine the width of the opening of the arch, w in meters at the base.
Solution
y = -(w - 6)2 + 16
width
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
The width of the opening is the difference of the x-intercepts, which occur when y = 0.
The roots are located at 10m, and 2m. The width of the base = 10 - 2 = 8m.
Parabola Word Problem
One of the stages at a major music festival has a parabola arch with a 40' base. The stage technicians need to install a giant 30' × 17' screen at the back, but need to not let the corners be cut off from view by the parabolic arch. The arch has a maximum height of exactly 264/7 feet. Can they install the screen successfully? If so, in what direction - horizontally or vertically?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
First determine an equation for the parabolic arch. Use the maximum at (20, 264/7) and the point (0, 0). You also have the point (40, 0) but don't need it.
Try the screen horizontal, so check the point on the parabola 5' from the left-most base...
This is too low, it needs to be at least 17' for the screen to fit this way.
Try the screen vertical, so check the point on the parabola 11.5' from the left-most base...
The screen is only 30' high, so it will fit when placed vertically.
Try the screen vertical, so check the point on the parabola 11.5' from the left-most base... The screen is only 30' high, so it will fit when placed vertically.
Applications of Quadratic Equations
A football player (wide receiver) has a maximum reach of 2m above the ground and can run 20m in the time a ball is thrown, starting at the same time. Given the equation, h(d) = -0.025x2 + 0.5x + 1.8, where h(d) is height in meters, and d is horizontal distance in meters, can the player catch the ball? Solve and show your work.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Plug in d = 20m and compare height of the ball h(d) with the height of the receiver (2m); if the ball is less then it can be caught.
Therefore, the ball is 1.8 m off the ground at a horizontal distance of 20m. The player can reach and catch the ball.
(Side note: the x-intercept of 23.1m is not used to determine if the ball can be caught because the player doesn't have to catch the ball at the ground. Another way to answer the question is to plug in 2.0m into the height to calculate the distance.)
(Side note: the x-intercept of 23.1m is not used to determine if the ball can be caught because the player doesn't have to catch the ball at the ground. Another way to answer the question is to plug in 2.0m into the height to calculate the distance.)
 |
Word Problems
Solve the following problems.
The product of two positive, consecutive numbers is 1806. What are the numbers?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Consecutive numbers can be written in terms of x as:
x, and (x + 1)
x = +42, -43
Since the numbers are positive, then x = +42
Then using the equation for the second number (x + 1), the other number is +43.
x, and (x + 1) x = +42, -43
Since the numbers are positive, then x = +42
Then using the equation for the second number (x + 1), the other number is +43.
The sum of the squares of two positive, consecutive integers is 481. Find the integers.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Consecutive integers can be written in terms of x as:
x, and (x + 1)
Using x = +16,
Then the two numbers are +16, + 17
x, and (x + 1) Using x = +16,
Then the two numbers are +16, + 17
A rectangle has a perimeter of 34 cm. Its area is 60 cm2. Sketch and determine the dimensions of the rectangle using algebra.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solve the system with two equations. Perimeter = 2x + 2y
Area = (x)(y)
x = 15, 5 cm ... (sketch not shown)
A really wide moat surrounds, and protects a castle. The castle has a rectangular footprint measuring 100 m by 70 m. The moat is an equal width all around. Determine the width of the moat to the nearest meter, if the sum of the area of the castle and the moat together is 90,000 m2.
Solution
width =
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
Write the expressions for the outside width and the outside length of the moat.
The outside width = 70 + 2x
The outside length = 100 + 2x
Solve for x using the quadratic equation: a = 4, b = 340, c = -83,000
The width of the moat is 107m.
(outside width = 284m, outside length = 314m)
The outside width = 70 + 2x
The outside length = 100 + 2x Solve for x using the quadratic equation: a = 4, b = 340, c = -83,000 The width of the moat is 107m.
(outside width = 284m, outside length = 314m)
A matte border of uniform width is to be placed around an Italian Renaissance painting with unknown width and length. The area of the matte border is to be twice the area of the painting. If the painting is 20 cm by 30 cm, then how wide should the border be?
Solution
width =
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
Write the expressions for the outside width and the outside length of the matte border.
The outside width = 20 + x
The outside length = 30 + x
Area of the border = 2(Area of the painting)
... use quadratic formula
x = 17.7, and -67.7
The width of the border should be 17.7 cm.
The outside width = 20 + x
The outside length = 30 + x Area of the border = 2(Area of the painting) ... use quadratic formula
x = 17.7, and -67.7
The width of the border should be 17.7 cm.
In a race, the Turtle is given a generous 30 minute head start. If the Turtle runs at 2 kilometers/hour, and the Rabbit runs at 8 kilometers/hour, then how many minutes after the Rabbit starts running will it catch up to the Turtle?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
minutes
Hint Unavailable
Let 't' be the time the rabbit does the race.
Turtle Rabbit
Distance same distance, d same distance, d
Speed 2 km/h 8 km/h
Time t + 0.5 t
Set the distances equal...
The rabbit will catch up to the turtle in ⅙ hour, or 10 minutes.
| Turtle | Rabbit | |
| Distance | same distance, d | same distance, d |
| Speed | 2 km/h | 8 km/h |
| Time | t + 0.5 | t |
The floor in a sports arena is 20 m by 40 m. If a 144 m2 section is to be removed along with an adjacent square piece, determine the possible dimensions of the square piece.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Let the small square sides be 'x' by 'x'.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Let the small square sides be 'x' by 'x'.
For the small known area of 144 m2, see that the side lengths are then (40 - x) and (x)...
The two possible side lengths for 'x' are 4m or 36m.
Or could be solved with method II...
For the small known area of 144 m2, see that the side lengths are then (40 - x) and (x)... The two possible side lengths for 'x' are 4m or 36m.
Or could be solved with method II...
Trigonometry with Right Triangles
(Review) Angles
The sum of the angles in a triangle is always 120˚.
Solution
Video
The sum of the angles in a triangle is always 180˚.
Interior Angle Algebra
The interior angles of a triangle are given in terms of x in the diagram below.

Determine x.
Solution
Video
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
˚
Hint Unavailable


Find y.
Solution
Video
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
˚
Hint Unavailable
x = 29˚
(Review) Triangle Side Lengths
Solve for the unknown side lengths, show your work.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Use the pythagorean theorem.
Use the pythagorean theorem. The hypotenuse (longest side) is 'c'.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use the pythagorean theorem.
Use the pythagorean theorem. The hypotenuse (longest side) is 'c'.
Solving Right Triangles
A right triangle has the following dimensions:
Base = xHeight = x + 7
Hypotenuse = 17
Substitute the side lengths into the pythagorean theorem and simplify the equation into standard form. Don't include spaces in your answer.
Solution
Video
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
= 0
Hint Unavailable

⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎

Factor the equation above to determine the possible length of the base, 'x'.
Solution
Video
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
x = -15, and x = +8
The side length cannot be negative, therefore x = 8
The side length cannot be negative, therefore x = 8
(Review) Cross Multiplication and Other Operations
Solve.
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
2 methods: multiply each by the lowest common multiple, or cross multiply.
Solve for 'a' by rearranging algebraically.
Solution
a =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Simplify,
Sides of a Right Triangle
The side defined as adjacent, 'a' can be on different sides of a triangle, like the top side, or the bottom side.
Solution

This is true, since the adjacent side is relative to where the angle is in the triangle.
Similar Triangles
Solve for length CE. Show your work.
Solution
Video
 CE =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
∆BAC ≈ ∆DAE
CE =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
∆BAC ≈ ∆DAE


Trig Ratios with Angles
Evaluate, using a calculator.
tan(45˚)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
tan(45˚) = 1
sin(30˚)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
sin(30˚) = 0.5
cos(0˚)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
cos(0˚) = 1
cos(60˚)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
sin(60˚) = 0.5
Trig Ratios with Ratios
Calculate the missing angle given the following ratios.
Solution
Video
θ =
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Solution
θ =
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Solution
θ =
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Solution
θ =
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Trig Triangles
Calculate side length AB and BC. (Round your answer to the nearest tenth decimal place.)
Solution
Video
 Hint
Clear
Info
AB = BC =
Incorrect Attempts:
CHECK
Hint Unavailable
Side length AB:
Side length BC:
Hint
Clear
Info
AB = BC =
Incorrect Attempts:
CHECK
Hint Unavailable
Side length AB:
Side length BC:
Calculate angle A.
Solution
Video
 A =
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
A =
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable


Given , determine the other two primary trig ratios. Use exact values, with positive lengths.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
First use Pythagorean Theorem to find the missing length. Since , the hypotenuse = 2, and one side is 1...
Use positive root,
Solving with Trig
Calculate angle 'n' if the area of the following triangle is 50 cm2.
Solution
Video
 n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
First find the height, h with the area of a triangle:
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
First find the height, h with the area of a triangle:
 Then solve for the angle, n using trig:
Then solve for the angle, n using trig:
 Then solve for the angle, n using trig:
Then solve for the angle, n using trig:
Solving with Trig
A heavy rain is being blown by strong winds at an angle of 25˚ 'from the vertical'. If the rain is directly blown (at a right angle when looking above) into a 15' bridge, determine the maximum distance under the bridge that the rain reaches.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
feet
Hint Unavailable
With a quick sketch (or a strong visual imagination) you can see that the right angle triangle has a 15' height, adjacent to the 25˚ angle. The distance 'into' the bridge is the base of the right angle triangle...
Solving with Trig
Determine the angle that the line y = ½x - 3 makes with the x-axis.
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Determine the side lengths of the right triangle and use trig ratios to solve...
(We could also just use the slope, 1/2 for the side lengths, and 2.)
Trig Word Problem
A very tall ladder is placed 20 m from the base of a building of unknown height, at an angle of elevation of 60˚ to the top of the building.

Determine the minimum length of ladder that must be used to get to the top of the building.
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
Angle = 60˚
Adjacent side length = 20 m
Solve for the ladder length, which is the hypotenuse:
∴ The ladder is 40 m in length. Wowzas
Adjacent side length = 20 m
Solve for the ladder length, which is the hypotenuse: ∴ The ladder is 40 m in length. Wowzas
How tall is the building? (Round your answer to the nearest decimal.)
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
The building height is opposite the 60˚ angle.
∴ The building is 34.6 m high.
Trig Word Problem
If the Cobain building is 20 m tall and the Statham building is 35 m tall, and the angle of depression from the top of Cobain to the bottom of Statham is 33˚, then determine the distance from the top of Cobain to the top of Statham.
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
First find the horizontal distance between the buildings. Draw the slanted line from the top of Cobain to the bottom of Statham.
Then find the distance (hypotenuse) between the tops...
Trig Word Problem
Gold coins are at the bottom of a diving pool, which is 14 m deep. A diver is underwater on the bottom of the pool, 20 m away from the coins and a swimmer is at the edge of the pool. The angle of depression from the swimmer to the coins is 45 degrees.

Assuming the swimmer and diver travel at the same speed (and they start going at the same time) determine the distance of the person who will get to the coins first.
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
Compare the direct distance between the swimmer (unknown hypotenuse) and the diver (20m) from the coins.
Make a triangle with angle 45˚, depth 14 m, and the direct distance of the swimmer, the hypotenuse:
∴ The swimmer is 19.8m, and the diver is 20m from the coins, since they travel at the same speed, the swimmer is closer to the gold coins so they will get to the coins first.
Make a triangle with angle 45˚, depth 14 m, and the direct distance of the swimmer, the hypotenuse:
∴ The swimmer is 19.8m, and the diver is 20m from the coins, since they travel at the same speed, the swimmer is closer to the gold coins so they will get to the coins first.
If the diver can travel 4.1 m/s, and the swimmer can swim 4 m/s, determine who will get to the coins first. Show your work on paper. (distance = speed × time) [1]
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
 Solve for t and compare using the d-s-t formula...
Time of the swimmer:
Solve for t and compare using the d-s-t formula...
Time of the swimmer:
Time of the diver:
∴ The diver gets to the gold coins first.
 Solve for t and compare using the d-s-t formula...
Time of the swimmer:
Solve for t and compare using the d-s-t formula...
Time of the swimmer:Time of the diver:
∴ The diver gets to the gold coins first.
Trig Word Problem
Use a variable to determine the height, h where distance is in meters. Round your answer to the nearest decimal place.
Solution
Video
 Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
Separate the big scalene triangle into 2 smaller right angle triangles.
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
Separate the big scalene triangle into 2 smaller right angle triangles.
 Let x be the base on the left. Make an equation for the left side using tan.
Let 30 - x be the base on the right. Make an equation for the right side.
Solve the system of equations: set the two h equations equal and solve for x:
Substitute x into any one of the equations to solve for h:
Let x be the base on the left. Make an equation for the left side using tan.
Let 30 - x be the base on the right. Make an equation for the right side.
Solve the system of equations: set the two h equations equal and solve for x:
Substitute x into any one of the equations to solve for h:
 Let x be the base on the left. Make an equation for the left side using tan.
Let 30 - x be the base on the right. Make an equation for the right side.
Solve the system of equations: set the two h equations equal and solve for x:
Substitute x into any one of the equations to solve for h:
Let x be the base on the left. Make an equation for the left side using tan.
Let 30 - x be the base on the right. Make an equation for the right side.
Solve the system of equations: set the two h equations equal and solve for x:
Substitute x into any one of the equations to solve for h:
Trig Word Problem
Some people are trying to measure the height of a super-tall statue. Point B is S 45˚ W from the bottom of the statue, and point C is E 45˚ S from the bottom. Let point A be the top of the statue and point D the bottom. ∆ABD and ∆ACD are in the vertical plane while ∆BDC is in the horizontal plane. The distance between point B and C is measured at 68 m.

If the angle of elevation from point B to the top is 24˚ and from point C to the top is 38˚, solve for DC
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
Solve the system of equations with 2 unknowns (variables): BD & DC...
Sub ② in ①...
Find another triangle where you can make an equation that only has BD and DC in it...
Solve for height AD.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
Much easier now that you have DC...
Trigonometry with Acute and Obtuse
Sine Law (for Acute and Obtuse Triangles)
Sine law is used to solve acute and obtuse triangles, which you otherwise couldn't using SOHCAHTOA.
Solving for the angles use...
- Lowercase represents side lengths (a, b, c, ...)
- Uppercase represents angles (A˚, B˚, C˚, ...)
- Use any two of the fractions/ratios
Solving for the side lengths use...
- Notice it's just the same as before, but reciprocated (flipped).
When do you use Sine law?
- Use Sine law any time you have this pair: 1 side length opposite 1 angle.
- You need 3 values to solve for the 4th unknown.
Some examples where you can solve for the red variable...
Cosine Law (for Acute and Obtuse Triangles)
Cosine law is used to solve acute and obtuse triangles, which you otherwise couldn't using SOHCAHTOA.
Solving for the side lengths use...
Solving for the angles use...
- Notice you're just rearranging the previous equations, isolating for the cos X˚... It's simple order of operations.
When do you use Cosine Law
- Any time you have 3 values, then you can solve for the 4th unknown.
Some examples where you can solve for the red variable...
You must use the quadratic equation when solving for these things...
Sine and Cosine Law
Which of the following would be used to solve for the first missing value on the triangle below?
Solution

There is an opposite angle-side pair here: 65˚ & 15.
Therefore use the Sine law first.

Therefore use the Sine law first.

Which of the following would be used first, to solve the triangle.
Solution

Use COSINE LAW when you have adjacent Side-Angle-Side (SAS), or Side-Side-Side (SSS).
In this case you have SAS so use:

In this case you have SAS so use:

Word Problems with Sine and Cosine Law
Daniel, a scuba diver, swims underwater 300 m north from the dive boat. He then turns right 120˚ and swims 400 m. How horizontally far from the boat is he, to the nearest meter? Round to the nearest tenth decimal. (A diagram is given here, but on a school test it might not be given so you would draw it.)
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
 Use cosine law
Use cosine law
 Use cosine law
Use cosine law
Sine and Cosine Law
An obtuse triangle has side lengths 10cm, 5cm, and 6cm.
Determine any one of the angles of the triangle. Round to the nearest tenth decimal place. [1]
Solution Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
An obtuse triangle is a triangle with one angle greater than 90˚ (an acute triangle is a triangle with all angles less than 90˚).
 The other angles are approximately 22.3˚ and 27.1˚
The other angles are approximately 22.3˚ and 27.1˚
 The other angles are approximately 22.3˚ and 27.1˚
The other angles are approximately 22.3˚ and 27.1˚
Calculate the area of the triangle.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm2
Hint Unavailable
You have side lengths and angles,
 First determine the height with a right angle triangle, using the one on the right-hand side here...
Then calculate the area,
First determine the height with a right angle triangle, using the one on the right-hand side here...
Then calculate the area,
 First determine the height with a right angle triangle, using the one on the right-hand side here...
Then calculate the area,
First determine the height with a right angle triangle, using the one on the right-hand side here...
Then calculate the area,
Word Problems with Sine and Cosine Law
From the top of a cliff, the angle of elevation to an airplane in the sky is 20˚. The angle of depression to a boat, directly under the plane, is 40˚. The distance from the boat to the top of the cliff is given. Find how high the plane is above the boat.
Solution
Video
 Hint
Clear
Info
Incorrect Attempts:
CHECK
km
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
km
Hint Unavailable
 Find the angle of the part of the smaller, upper triangle at the plane:
The total angle at the cliff is 60˚ (20˚ + 40˚).
Find the angle of the part of the smaller, upper triangle at the plane:
The total angle at the cliff is 60˚ (20˚ + 40˚).
Use the sine law to find the height of the plane above the boat using the whole, large triangle (let C equal the distance PB from the plane to the boat):
 Find the angle of the part of the smaller, upper triangle at the plane:
The total angle at the cliff is 60˚ (20˚ + 40˚).
Find the angle of the part of the smaller, upper triangle at the plane:
The total angle at the cliff is 60˚ (20˚ + 40˚).Use the sine law to find the height of the plane above the boat using the whole, large triangle (let C equal the distance PB from the plane to the boat):
Word Problems with Sine and Cosine Law
Two buildings are 40 m apart. David and Helen work in adjacent office buildings. Use the given information to determine the height of Helen’s window. The angle of depression from David’s window to the base of Helen’s building is 33 degrees. The angle of elevation from David’s window to Helen’s window is 20 degrees.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
The following is just one way of solving it using the sine law, you may get the right answer with various other approaches (including right triangles):
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
The following is just one way of solving it using the sine law, you may get the right answer with various other approaches (including right triangles):
The total angle at David is 53˚ (20˚ + 33˚).
Calculate the distance from David to the ground:
Calculate the angle at Helen's window
Calculate
The total angle at David is 53˚ (20˚ + 33˚).
Calculate the distance from David to the ground: Calculate the angle at Helen's window Calculate
Word Problems with Sine and Cosine Law
Solve for length, AB. (Round your answer to the nearest tenth of a meter).
Solution
Video
 AB =
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
Calculate angle ANB:
Calculate length BN:
Then calculate length AB using the sine law:
AB =
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
Calculate angle ANB:
Calculate length BN:
Then calculate length AB using the sine law:
Word Problems with Sine and Cosine Law
Calculate length, x.
Solution
 x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
First find height, to use for finding 'x' later...
Then calculate 'x'...
... But actually this can be done another way, quicker...
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
First find height, to use for finding 'x' later...
Then calculate 'x'...
... But actually this can be done another way, quicker...
Word Problems with Sine and Cosine Law
Given the complex shape, determine the missing quantities stated below.

