GRADE
5/6
Math
Students are expected to build on their knowledge from the previous year, at a higher level of complexity. The depth of concepts, mathematical procedures and processes will be expanded each year. Elementary school is an important time in your child's academic development. Find out how an individualized approach to learning can build the skills, habits and attitudes your child needs for a solid academic foundation and a lifetime of success. Prerequisite: Math 5
TABLE OF CONTENTS
Practice Multiplication & Division
| 1 × 0 |
| 0 |
| 1 × 1 |
| 1 |
| 1 × 2 |
| 2 |
| 2 × 2 |
| 4 |
| 2 × 3 |
| 6 |
| 2 × 4 |
| 8 |
| 2 × 5 |
| 10 |
| 2 × 6 |
| 12 |
| 2 × 7 |
| 14 |
| 2 × 8 |
| 16 |
| 2 × 9 |
| 18 |
| 2 × 10 |
| 20 |
| 2 × 11 |
| 22 |
| 2 × 12 |
| 24 |
| 3 × 1 |
| 3 |
| 3 × 2 |
| 6 |
| 3 × 3 |
| 9 |
| 3 × 4 |
| 12 |
| 3 × 5 |
| 15 |
| 3 × 6 |
| 18 |
| 3 × 7 |
| 21 |
| 3 × 8 |
| 24 |
| 3 × 9 |
| 27 |
| 3 × 10 |
| 30 |
| 3 × 11 |
| 33 |
| 3 × 12 |
| 36 |
| 4 × 1 |
| 4 |
| 4 × 2 |
| 8 |
| 4 × 3 |
| 12 |
| 4 × 4 |
| 16 |
| 4 × 5 |
| 20 |
| 4 × 6 |
| 24 |
| 4 × 7 |
| 28 |
| 4 × 8 |
| 32 |
| 4 × 9 |
| 36 |
| 4 × 10 |
| 40 |
| 4 × 11 |
| 44 |
| 4 × 12 |
| 48 |
| 5 × 1 |
| 5 |
| 5 × 2 |
| 10 |
| 5 × 3 |
| 15 |
| 5 × 4 |
| 20 |
| 5 × 5 |
| 25 |
| 5 × 6 |
| 30 |
| 5 × 7 |
| 35 |
| 5 × 8 |
| 40 |
| 5 × 9 |
| 45 |
| 5 × 10 |
| 50 |
| 5 × 11 |
| 55 |
| 5 × 12 |
| 60 |
| 6 × 1 |
| 6 |
| 6 × 2 |
| 12 |
| 6 × 7 |
| 42 |
| 6 × 8 |
| 48 |
| 6 × 9 |
| 54 |
| 6 × 10 |
| 60 |
| 6 × 11 |
| 66 |
| 6 × 12 |
| 72 |
| 7 × 1 |
| 7 |
| 7 × 2 |
| 14 |
| 7 × 3 |
| 21 |
| 7 × 4 |
| 28 |
| 7 × 5 |
| 35 |
| 7 × 6 |
| 42 |
| 7 × 7 |
| 49 |
| 7 × 8 |
| 56 |
| 7 × 9 |
| 63 |
| 7 × 10 |
| 70 |
| 7 × 11 |
| 77 |
| 7 × 12 |
| 84 |
| 8 × 1 |
| 8 |
| 8 × 2 |
| 16 |
| 8 × 3 |
| 24 |
| 8 × 4 |
| 32 |
| 8 × 5 |
| 40 |
| 8 × 6 |
| 48 |
| 8 × 7 |
| 56 |
| 8 × 8 |
| 64 |
| 8 × 9 |
| 72 |
| 8 × 10 |
| 80 |
| 8 × 11 |
| 88 |
| 8 × 12 |
| 96 |
| 9 × 1 |
| 9 |
| 9 × 2 |
| 18 |
| 9 × 3 |
| 27 |
| 9 × 4 |
| 36 |
| 9 × 5 |
| 45 |
| 9 × 6 |
| 54 |
| 9 × 7 |
| 63 |
| 9 × 8 |
| 72 |
| 9 × 9 |
| 81 |
| 9 × 10 |
| 90 |
| 9 × 11 |
| 99 |
| 9 × 12 |
| 108 |
| 10 × 1 |
| 10 |
| 10 × 2 |
| 20 |
| 10 × 3 |
| 30 |
| 10 × 4 |
| 40 |
| 10 × 5 |
| 50 |
| 10 × 6 |
| 60 |
| 10 × 7 |
| 70 |
| 10 × 8 |
| 80 |
| 10 × 9 |
| 90 |
| 10 × 10 |
| 100 |
| 10 × 11 |
| 110 |
| 10 × 12 |
| 120 |
| 11 × 1 |
| 11 |
| 11 × 2 |
| 22 |
| 11 × 3 |
| 33 |
| 11 × 4 |
| 44 |
| 11 × 5 |
| 55 |
| 11 × 6 |
| 66 |
| 11 × 7 |
| 77 |
| 11 × 8 |
| 88 |
| 11 × 9 |
| 99 |
| 11 × 10 |
| 110 |
| 11 × 12 |
| 132 |
| 12 × 1 |
| 12 |
| 12 × 2 |
| 24 |
| 12 × 3 |
| 36 |
| 12 × 4 |
| 48 |
| 12 × 5 |
| 60 |
| 12 × 6 |
| 72 |
| 12 × 7 |
| 84 |
| 12 × 8 |
| 96 |
| 12 × 9 |
| 108 |
| 12 × 10 |
| 120 |
| 12 × 11 |
| 132 |
| 12 × 12 |
| 144 |
| 4 ÷ 2 |
| 2 |
| 6 ÷ 3 |
| 2 |
| 6 ÷ 2 |
| 3 |
| 9 ÷ 3 |
| 3 |
| 8 ÷ 2 |
| 4 |
| 8 ÷ 4 |
| 2 |
| 12 ÷ 3 |
| 4 |
| 12 ÷ 4 |
| 3 |
| 16 ÷ 4 |
| 4 |
| 10 ÷ 5 |
| 2 |
| 10 ÷ 2 |
| 5 |
| 15 ÷ 3 |
| 5 |
| 15 ÷ 5 |
| 3 |
| 20 ÷ 4 |
| 5 |
| 20 ÷ 5 |
| 4 |
| 25 ÷ 5 |
| 5 |
| 12 ÷ 2 |
| 6 |
| 12 ÷ 6 |
| 2 |
| 18 ÷ 3 |
| 6 |
| 18 ÷ 6 |
| 3 |
| 24 ÷ 6 |
| 4 |
| 24 ÷ 4 |
| 6 |
| 30 ÷ 5 |
| 6 |
| 30 ÷ 6 |
| 5 |
| 36 ÷ 6 |
| 6 |
| 14 ÷ 2 |
| 7 |
| 14 ÷ 7 |
| 2 |
| 21 ÷ 3 |
| 7 |
| 21 ÷ 7 |
| 3 |
| 28 ÷ 4 |
| 7 |
| 28 ÷ 7 |
| 4 |
| 35 ÷ 7 |
| 5 |
| 35 ÷ 5 |
| 7 |
| 42 ÷ 7 |
| 6 |
| 42 ÷ 6 |
| 7 |
| 49 ÷ 7 |
| 7 |
| 16 ÷ 2 |
| 8 |
| 16 ÷ 8 |
| 2 |
| 24 ÷ 8 |
| 3 |
| 24 ÷ 3 |
| 8 |
| 32 ÷ 4 |
| 8 |
| 32 ÷ 8 |
| 4 |
| 40 ÷ 8 |
| 5 |
| 40 ÷ 5 |
| 8 |
| 48 ÷ 6 |
| 8 |
| 48 ÷ 8 |
| 6 |
| 56 ÷ 7 |
| 8 |
| 56 ÷ 8 |
| 7 |
| 64 ÷ 8 |
| 8 |
| 18 ÷ 2 |
| 9 |
| 18 ÷ 9 |
| 2 |
| 27 ÷ 3 |
| 9 |
| 27 ÷ 9 |
| 3 |
| 36 ÷ 4 |
| 9 |
| 36 ÷ 9 |
| 4 |
| 45 ÷ 5 |
| 9 |
| 45 ÷ 9 |
| 5 |
| 54 ÷ 6 |
| 9 |
| 54 ÷ 9 |
| 6 |
| 63 ÷ 7 |
| 9 |
| 63 ÷ 9 |
| 7 |
| 72 ÷ 8 |
| 9 |
| 72 ÷ 9 |
| 8 |
| 81 ÷ 9 |
| 9 |
| 20 ÷ 10 |
| 2 |
| 20 ÷ 2 |
| 10 |
| 30 ÷ 3 |
| 10 |
| 30 ÷ 10 |
| 3 |
| 40 ÷ 4 |
| 10 |
| 40 ÷ 10 |
| 4 |
| 50 ÷ 5 |
| 10 |
| 50 ÷ 10 |
| 5 |
| 60 ÷ 6 |
| 10 |
| 60 ÷ 10 |
| 6 |
| 70 ÷ 7 |
| 10 |
| 70 ÷ 10 |
| 7 |
| 80 ÷ 8 |
| 10 |
| 80 ÷ 10 |
| 8 |
| 90 ÷ 9 |
| 10 |
| 90 ÷ 10 |
| 9 |
| 100 ÷ 10 |
| 10 |
| 22 ÷ 2 |
| 11 |
| 22 ÷ 11 |
| 2 |
| 33 ÷ 11 |
| 3 |
| 33 ÷ 3 |
| 11 |
| 44 ÷ 4 |
| 11 |
| 44 ÷ 11 |
| 4 |
| 55 ÷ 5 |
| 11 |
| 55 ÷ 11 |
| 5 |
| 66 ÷ 6 |
| 11 |
| 66 ÷ 11 |
| 6 |
| 77 ÷ 7 |
| 11 |
| 77 ÷ 11 |
| 7 |
| 88 ÷ 8 |
| 11 |
| 88 ÷ 11 |
| 8 |
| 99 ÷ 9 |
| 11 |
| 99 ÷ 11 |
| 9 |
| 110 ÷ 11 |
| 10 |
| 110 ÷ 10 |
| 11 |
| 121 ÷ 11 |
| 11 |
| 24 ÷ 12 |
| 2 |
| 24 ÷ 2 |
| 12 |
| 36 ÷ 3 |
| 12 |
| 36 ÷ 12 |
| 3 |
| 48 ÷ 4 |
| 12 |
| 48 ÷ 12 |
| 4 |
| 60 ÷ 5 |
| 12 |
| 60 ÷ 12 |
| 5 |
| 72 ÷ 6 |
| 12 |
| 72 ÷ 12 |
| 6 |
| 84 ÷ 7 |
| 12 |
| 84 ÷ 12 |
| 7 |
| 96 ÷ 8 |
| 12 |
| 96 ÷ 12 |
| 8 |
| 108 ÷ 9 |
| 12 |
| 108 ÷ 12 |
| 9 |
| 120 ÷ 10 |
| 12 |
| 120 ÷ 12 |
| 10 |
| 132 ÷ 11 |
| 12 |
| 132 ÷ 12 |
| 11 |
| 144 ÷ 12 |
| 12 |
INCORRECT
Number Sense and Numeration
Word Expressions
Calculate each of the following expressions.
Six hundred and forty eight more than three thousand and one.
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Align the place columns correctly...
Align the place columns correctly...
= 3649
Hint
Clear
Info
Incorrect Attempts:
CHECK
Align the place columns correctly...
Thirty thousand three hundred fifty two less than fifty thousand five hundred.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Align the place columns correctly...
Align the place columns correctly...
= 20,148
Hint
Clear
Info
Incorrect Attempts:
CHECK
Align the place columns correctly...
Vertical Place Value Columns with Addition and Subtraction
Practice your addition and subtraction any way you like using mental math, or without the use of a calculator. Make sure to show your work.
Subtract: 700 - 7
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
... = 693
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Subtract: 560 - 80
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Subract 60 from 560 and 80...
Borrow from the 100's column, 5-- becomes 4--...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Add: 4,000 + 500 + 60 + 8
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
... = 4,568
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Subtract: 4,568 - 3,000 - 500 - 70 - 3
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Step-by-step (for each place value)...
= 1,568
= 1,068
= 998
= 995
(Yes you could just do 4,568 - 3,573...)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(Yes you could just do 4,568 - 3,573...)
Ordering Whole Numbers with Place Values
Indicate whether the following statement is true or false:
Solution
Video
589,301 > 589,199
True. Start comparing the place values (ones, tens, hundreds...) from the LEFT-HAND side... (in the hundreds column) 3 is bigger than 9...
Ordering Decimals
Order the following decimals from greatest to least going from top to bottom.
Solution
0.999
0.90
0.009
1.005
0.88
1.001
0.0095
Compare the place values: ones, tenths, hundredths, thousandths...
1.005, 1.001, 0.999, 0.90, 0.88, 0.0095, 0.009
Can also be written as
1.005 > 1.001 > 0.999 > 0.90 > 0.88 > 0.0095 > 0.009
(comparing the last two, to see more easily, you can change to: 0.0095 > 0.0090)
0.999
0.90
0.009
1.005
0.88
1.001
0.0095
1.005, 1.001, 0.999, 0.90, 0.88, 0.0095, 0.009
Can also be written as
1.005 > 1.001 > 0.999 > 0.90 > 0.88 > 0.0095 > 0.009
(comparing the last two, to see more easily, you can change to: 0.0095 > 0.0090)
Representing Numbers up to 1,000,000
Which of the following is the correct word number for the following?
Solution
220,012
Two hundred twenty thousand and twelve
Which of the following is the correct phrase for the following number?
Solution
502,401
Five hundred and two thousand four hundred and one
Which of the following is the correct number?
Solution
Eighty-two thousand four hundred and forty-four
82,444
Comparing Decimals
In a 300 meter race, Julie finished in 45.42 seconds. Christine finished in 44.51 seconds, Alice finished in 42.08 seconds, and Sarah finished in 42.24 seconds.
Who came in last?
Solution
Julie had the longest time, so she came in last.
How much time was between the first and last place?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
seconds
Hint Unavailable
Alice finished first: 42.08 seconds
Julie finished last: 45.42 seconds
= 45.42 - 42.08
= 3.34
Hint
Clear
Info
Incorrect Attempts:
CHECK
seconds
Hint Unavailable
Julie finished last: 45.42 seconds
= 45.42 - 42.08
= 3.34
Comparing Decimals
Compare the following by filling in the blanks.
0.5 ____ 0.409
Solution
0.5 > 0.409
62.37 ____ 62.370
Solution
62.37 = 62.370
21.89 ____ 21.95
Solution
21.89 < 21.95
Rounding Decimals
Round to the nearest hundredth.
234.2123
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Example: 0.5 has a five in the "tenths" column and a zero in the "ones" column
234.21
Hint
Clear
Info
Incorrect Attempts:
CHECK
Example: 0.5 has a five in the "tenths" column and a zero in the "ones" column
10,000.95
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
5 or more rounds up...
10,001
Hint
Clear
Info
Incorrect Attempts:
CHECK
5 or more rounds up...
Converting Decimals and Fractions
Convert 0.75 to a fraction (remember to reduce fully).
Solution
Converting Decimals and Fractions
Convert to a decimal.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
2.5
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Equivalent Fraction (Multiplying by "1")
Solve, without reducing.
What fraction is equivalent to ?
Solution
You can multiply the top (numerator) and bottom (denominator) by the same amount... 11
Determine the answer.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Determine parts of each fraction.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Determine the first fraction.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
It's all or nothing now!
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Fractions
David has $100. He spends of it on a soccer ball. How much does he have left?
Solution
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
25
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Fraction and Percent Word Problems
Jon wins $100. He gives 50% to his mother, and from what is left over after giving money to his mother, he gives to charity. How much does Jon give to charity?
Solution
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
20 [steps not shown here]
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Comparing Fractions
Compare the following by filling in the blank (without using a calculator).
Solution
Make a common denominator in order to compare. Use the lowest common multiple (LCM) of 6 & 4: 12...
Solution
Video


Solution
Video
Make a common denominator (with the lowest common multiple, LCM)
Multiples of 3: 3, 6, 9, 12, 15, ...
Multiples of 5: 5, 10, 15, ...
Therefore
Multiples of 3: 3, 6, 9, 12, 15, ...
Multiples of 5: 5, 10, 15, ...
Therefore
Prime and Composite Numbers
Which of the following is not a prime number?
Solution
Prime numbers can only be divided by one and themselves. Composite numbers can be factored into several prime numbers.
Factors and Multiples
The following numbers are factors of 22
Solution
Video
22, 44, 66, 88, 110
These are multiples of 22. Multiples multiply, going up higher each time... There are infinite amount of multiples...
(There are only a certain amount of factors... for 22 it's: 1, 2, 11, 22)
(There are only a certain amount of factors... for 22 it's: 1, 2, 11, 22)
Determine the missing factor of 36:
Solution
1, 2, 3, 4, 6, 9, 12, 18
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
36 is a factor of 36 because you can divide 36 by 36.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Adding, Subtracting, Multiplying, and Dividing Fractions
Simplify the following fraction expressions without the use of a calculator. Reduce your answer fully.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Make the denominator with the lowest common multiple (LCM)...
4 → 8 → 12 → 16 →
5 → 10 → 15 →
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
4 → 8 → 12 → 16 →
5 → 10 → 15 →
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Make the denominator with the lowest common multiple (LCM)...
3 → 6 → 9 →
2 → 4 → 6 → 8 → 10 →
4 → 8 →
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
3 → 6 → 9 →
2 → 4 → 6 → 8 → 10 →
4 → 8 →
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
You don't need a common denominator for multiplying fractions, look it's easy!
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
With multiplication of fractions you can cancel something once on the top and bottom...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
With division of fractions... multiply by the reciprocal of the fraction after the division sign ÷...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
With division of fractions... multiply by the reciprocal of the fraction after the division sign ÷ ... And cancel across division...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
More Fractions with Order of Operations (PEMDAS/BEDMAS)
Simplify the following fraction expressions without the use of a calculator. Reduce your answer fully.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
...FRACTIONS HOMEWORK (GR6)
Simplify the following fraction expressions without the use of a calculator. Reduce your answer fully.
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Adding Fractions Word Problems
David walks km home from a soccer game, then walks km to the corner store to buy a treat, then he walks km to his friends house. How far has David travelled in total?
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
To add fractions, make a common denominator... the lowest common multiple (LCM)
In this case the LCM is 20...
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
In this case the LCM is 20...
Mixed Fractions - Basics
True or false?
Solution
Careful, look at each one closely,
Adding & Subtracting Mixed Fractions
Given the following 3 different examples of ways to solve, use whatever method you prefer, and enter your answer as a fully reduced, mixed fraction.
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Just method #1 is shown here...
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
The Commutative Property
The following expressions are equal
5 ÷ 6 × 18 = 5 × 18 ÷ 6
Solve the following, without the use of a calculator
Solution
3 ÷ 11 × 55
The following expression equals 3100
Solution
3100 ÷ 999 × 999
3100 ÷ 999 × 999
= 3100 × 999 ÷ 999
= 3100 × 1
= 3100
= 3100 × 999 ÷ 999
= 3100 × 1
= 3100
The Distributive Property
The following is correct...
Solution
Yup, this is how the 'distributive property' works.
Try calculating the following using the distributive property, without the use of a calculator
Solution
(5.5) × 8
Adding Decimals
Add the following decimals without the use of a calculator...
10,240.15 + 29.1
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Make sure to line up all the decimals overtop of eachother...
= 10269.25
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
6.99 + 10.01 + 1.3 + 5.22 + 0.05 + 0.25
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Make sure to line up all the decimals overtop of eachother...
= 23.82
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
2.640 + 34.3 + 0.06
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Make sure to line up all the decimals overtop of eachother (shown above)
You could use placeholder zeros:
... = 37
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
You could use placeholder zeros: ... = 37
Subtracting Decimals
Subtract: 391,246.123 - 123.4
Solution
Video
Make sure to line up all the decimals overtop of eachother
You could use placeholder zeros:
= 391, 122.723
Multiplying by Factors of 10
Find and state the pattern in the following.
Solution
As you divide by a smaller factor of ten each time, the decimal place moves one place to the right, and the resulting number gets bigger.
Solution
As you multiply by a smaller factor of ten each time, the decimal place moves one place to the left, and the resulting number gets smaller.
Multiplying and Dividing by Factors of 10
Match each operation below with the other operation that does the same thing.
Solution
× 0.1
÷ 0.01
÷ 0.1
× 100
÷ 10
× 10
× 0.1 = ÷ 10
÷ 0.01 = × 100
For example:
55 × 0.1 = 5.5
55 ÷ 10 = 5.5
33 ÷ 0.01 = 3300
33 × 100 = 3300
× 0.1
÷ 0.01
÷ 0.1
× 100
÷ 10
× 10
÷ 0.01 = × 100
For example:
55 × 0.1 = 5.5
55 ÷ 10 = 5.5
33 ÷ 0.01 = 3300
33 × 100 = 3300
Starting with the number below, drag and drop each operation into the box with the correct answer.
Solution
1525
× 10
÷ 0.01
× 0.1
÷ 100
= 15.25
= 152.5
= 15250
= 152500
As you multiply by a smaller factor of ten each time, the decimal place moves one place to the left, and the resulting number gets smaller.
As you divide by a smaller factor of ten each time, the decimal place moves one place to the right, and the resulting number gets bigger.
× 10
÷ 0.01
× 0.1
÷ 100
= 15.25
= 152.5
= 15250
= 152500
As you divide by a smaller factor of ten each time, the decimal place moves one place to the right, and the resulting number gets bigger.
Multiply Whole Numbers
Solve, without the use of a calculator.
25 * 200 =
Solution
First take care of the integers
(25)(2) = 50
Then add the zeros at the end of 2 0 0...
5 0 0 0
Multiply Decimal Numbers by 10, 100, 1000, and 10000
Solve, without the use of a calculator.
5.2513 × 100 =
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Move the decimal by the number of zeros in the number, 1 0 0, so by 2 zeros. Think: move the decimal to the right to make the number bigger, because you are multiplying by one hundred...
= 525.13
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
2.3 × 1000 =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Dividing Numbers by 10, 100, 1000, and 10000
Solve, without the use of a calculator.
345,000 ÷ 1,000 =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
15,000 ÷ 50
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Multiply Whole Numbers by 0.1, 0.01, and 0.001
Solve, without the use of a calculator.
25 × 0.1 =
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Count the number of places, behind the decimal,
0.1
There is one place behind the decimal,
25.
Move the decimals in the question by the same amount,
2.5
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
123456 × 0.001 =
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Count the number of places, behind the decimal,
0.001
There are three places behind the decimal,
123456.
Move the decimals in the question by the same amount,
123.456
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
200 × 0.001 =
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Count the number of places, behind the decimal,
0.001
There are three places behind the decimal,
200.
Move the decimals in the question by the same amount,
0.200
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Multiply Decimal Numbers by Whole Numbers
The rules for multiplying decimals are:
- Count the total number of decimal places in the numbers (your magic number).
- Multiply normally, as if without decimals
- Once you have the final product, put the decimal at the furthest position to the right
- Move the decimal to the left by the total number of decimal places (your magic number).
Multiply the following without the use of a calculator.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Count the total number of decimal places in 30.31 and 5.00 = 2 + 2 = 4 decimal places.
Move the decimal 4 places left.
= 151.550̸0̸
= 151.55
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Move the decimal 4 places left.
= 151.550̸0̸
= 151.55
Multiplying Decimals
Remember, the rules for multiplying decimals are:
- Count the total number of decimal places in the numbers (your magic number).
- Multiply normally, as if without decimals
- Once you have the final product, put the decimal at the furthest position to the right
- Move the decimal to the left by the total number of decimal places (your magic number).
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Count the total number of decimal places
= 1 + 1 = 2 decimal places.
Move the decimal, by the same places as the question, 2 places left.
= 26.52
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
= 1 + 1 = 2 decimal places.
Move the decimal, by the same places as the question, 2 places left.
= 26.52
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Count the total number of decimal places
= 2 + 1 = 3 decimal places.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
= 2 + 1 = 3 decimal places.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Count the total number of decimal places
= 2 + 2 = 4 decimal places.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
= 2 + 2 = 4 decimal places.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Count the total number of decimal places
= 3 decimal places.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
= 3 decimal places.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Count the total number of decimal places
= 3 decimal places.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
= 3 decimal places.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Count the total number of decimal places
= 1 + 4 = 5 decimal places.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
= 1 + 4 = 5 decimal places.
Divide Whole Numbers by 0.1, 0.01, and 0.001
Dividing whole numbers by decimal factors of ten (0.1, 0.01, and 0.001...) will make the number in your answer bigger.
The decimal place will move 3 times in the expression below.
Solution
21.5 ÷ 0.001
0 . 0 0 1
÷ means move the decimal to the right.
Set up the number by adding more zeros on the end. See how this does not change the number yet, it's still twenty-one point five.
Then move the decimal place over in the correct direction, and the correct amount of times.
That's it!
The number is 21,500
÷ means move the decimal to the right.
Set up the number by adding more zeros on the end. See how this does not change the number yet, it's still twenty-one point five. Then move the decimal place over in the correct direction, and the correct amount of times. That's it!
The number is 21,500
The following is correct.
Solution
11.5 ÷ 0.001 = 11500
÷ 0 . 0 0 1 means move the decimal three times, to the right...
11.5 ÷ 0.001 = 11500
11.5 ÷ 0.001 = 11500
The following is correct.
Solution
22.3 ÷ 0.01 = 22300
22.3 ÷ 0.01 = 2230
÷ 0 . 0 1 means move the decimal twice, to the right.
÷ 0 . 0 1 means move the decimal twice, to the right.
What does the following equal?
Solution
432.1098 ÷ 0.00001
Move the decimal place to the right, making the number bigger.
Move the decimal 5 times: 0 . 0 0 0 0 1
Move the decimal 5 times: 0 . 0 0 0 0 1
Dividing Decimals
Solve the questions below using the following example as a guide.
26.64 ÷ 1.2
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Convert the decimals first: move both 2 spaces...
Then, long division... (make sure to place the decimal directly above)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
4.263 ÷ 0.21
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Convert the decimals first: move both 2 spaces...
Then, long division... (make sure to place the decimal directly above)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
2.5235 ÷ 0.0035
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Convert the decimals first: move both 4 spaces...
Then, long division...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Estimation with Addition & Subtraction
Use estimation and mental math to determine the most accurate answer. Some examples of estimation according to current curriculum guidelines:
8 ≈ 1022 ≈ 20
113 ≈ 100
562 ≈ 1,000
1,200 ≈ 1,000
19,201 ≈ 20,000
132,092 ≈ 100,000
55 + 105 + 37
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The curriculum says 105 should round to 100, the nearest largest place value.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
999 - 113 - 25
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
1025 - 175 - 63
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
4535 - 2590
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
3567 - 2631
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
128,120 + 282,123
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Estimation with Multiplication & Division
A student collected 223 pop bottles for a recycling program at the school. If the pop bottles were collected over 4 days, then on average how many were collected each day?
Solution
A little bit more than 200 ÷ 4 = 50
...which is a bit more than 50
...which is ≈ 55
...which is a bit more than 50
...which is ≈ 55
Unit Rates and Dividing Decimals by Whole Numbers
A calculator costs $8.50 at The Bookey School Supply Store. If another store, The Penney Store, is selling 5 calculators for $46.25 what is the price for one calculator at The Penney Store, and which store has the better deal?
Solution
Order of Operations (PEMDAS, BEDMAS)
Simplify the following, without the use of a calculator.
Solution
6 x (4 ÷ 2) + 8 + (10 + 4) – 2 × 6
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Use PEMDAS/BEDMAS...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
3 × 4 ÷ 3 × 4 × (64 ÷ 16)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Use PEMDAS/BEDMAS...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Video
(4 × 2) + 32 - 4 ÷ 2
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Use PEMDAS/BEDMAS...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Ratios
A bubble gum container holds 24 blue and 32 red gumballs. What is the ratio of red to blue?
Fill in the missing number below to make the ratios equal:
2 to 5 = ___ to 20
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Converting Decimals, Fractions, and Percents
Fill in the blank.
Solution
| Fraction | Percent |
| 50 % | |
| 75 % | |
| 10% |
Hint
Clear
Info
Incorrect Attempts:
CHECK
%
Hint Unavailable
| Fraction | Percent |
| 50 % | |
| 75 % | |
| 40 % | |
| 10% |
Solution
| Decimal | Percent |
| 0.3 | 30% |
| 0.25 | 25% |
| 5% | |
| 0.01 | 1% |
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
| Decimal | Percent |
| 0.3 | 30% |
| 0.25 | 25% |
| 0.05 | 5% |
| 0.01 | 1% |
Measurement
Time
Which of the following is the longest time when you set something in a microwave and enter a time (in minutes:seconds)?
Solution
0:90 or 90 seconds is actually longer than 1:00 or 1 minute, which is only 60 seconds.
Appropriate Metric Units: Millimeter, Centimeter, Decimeter, Meter, Decameter, Kilometer
Which of the following units of measurement would be most appropriate for measuring the height of your refrigerator?
Converting Metric Units of Distance
Match the units of meters to the equivalent units of kilometers given that 1000 m = 1 km.
Solution
990 m
9,000 m
99 m
0.99 m
9 km
0.099 km
0.99 km
0.0099 km
Make sure the number of kilometers is always a factor of 1,000 lower than the number of meters.
9 km = 9,000 m
0.9 km = 900 m
(The 'km' moves down one place value, so the 'm' moves down one place value as well)
990 m
9,000 m
99 m
0.99 m
9 km
0.099 km
0.99 km
0.0099 km
9 km = 9,000 m
0.9 km = 900 m
(The 'km' moves down one place value, so the 'm' moves down one place value as well)
Converting Metric Units of Distance, Practice
Convert the following, given:
| Pair A: | 1,000 m | 1 km |
| Pair B: | 100 cm | 1 m |
| Pair C: | 10 mm | 1 cm |
5,015.02 m = _____________ km
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
km
Hint Unavailable
Move the decimal by three, to the left.
Hint
Clear
Info
Incorrect Attempts:
CHECK
km
Hint Unavailable
10.019 m = _____________ km
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
km
Hint Unavailable
Move the decimal by three, to the left.
Hint
Clear
Info
Incorrect Attempts:
CHECK
km
Hint Unavailable
0.0234 km = _____________ m
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
Move the decimal by three, to the right.
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
1235.2 km = _____________ m
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
Move the decimal by three, to the right.
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
1245 mm = _____________ cm
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
Move the decimal by one place, to the left.
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
0.003 cm = _____________ mm
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
mm
Hint Unavailable
Move the decimal by one, to the right.
Hint
Clear
Info
Incorrect Attempts:
CHECK
mm
Hint Unavailable
0.015 cm = _____________ m
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
Move the decimal by two, to the left.
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
12,585.0 mm = _____________ km
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
km
Hint Unavailable
You can do it all at once, or split it into steps like this,
12,585.0 mm = _____________ cm
Move the decimal by one, to the left.
12,58.50 cm = _____________ m
Move the decimal by two, to the left.
12.5850 m = _____________ km
Move the decimal by three, to the left.
= 0.012585 km
Hint
Clear
Info
Incorrect Attempts:
CHECK
km
Hint Unavailable
Units
The prefix milli (m-) means one thousandth.
So, 100 mm = 1 m.
Solution
Video
There are 1,000 mm in 1 m.
Match each measurement with its equivalent.
Solution
Video
1,000 mm
1,000 mL
1,000 mg
1 L
1 m
1 g
None of them
1,000 mL = 1 L
1,000 mg = 1 g
1,000 mm - 1 m
1,000 mm
1,000 mL
1,000 mg
1 L
1 m
1 g
None of them
1,000 mg = 1 g
1,000 mm - 1 m
Convert 7.5 kilograms, kg into grams, g.
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
grams
Hint Unavailable
To go from kilograms (kg) to grams (g) to milligrams (mg):
or the other way around, from milligrams (mg) to grams (g) to kilograms (kg)...
Move the decimal place 3 times to the right when multiply 1000.
Hint
Clear
Info
Incorrect Attempts:
CHECK
grams
Hint Unavailable
Units
The prefix kilo (k-) means one thousand.
There are 100 m in 1 km.
Solution
There are 1,000 m in 1 km.
Match each measurement with its equivalent.
Solution
2 km
5 kg
200 m
2,000 m
500 g
5,000 g
2 km = 2,000 m
5 kg = 5,000 g
2 km
5 kg
200 m
2,000 m
500 g
5,000 g
5 kg = 5,000 g
Convert 75.0 m into kilometers (km).
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
kilometers
Hint Unavailable
When you divide by 1000, move the decimal 3 spaces to the left.
Hint
Clear
Info
Incorrect Attempts:
CHECK
kilometers
Hint Unavailable
Converting Metric Units of Mass
Fill in the blank, given that 1000 g = 1 kg
| Grams (g) | Kilograms (kg) |
| 220 | 0.22 |
| 0.5 | |
| 12,500 | 12.5 |
Hint
Clear
Info
Incorrect Attempts:
CHECK
grams
Hint Unavailable
Converting Metric Units of Volume
Fill in the blank, given that 1000 mL = 1 L
| Milliliters (mL) | Liters (L) |
| 4 | 0.004 |
| 34 | |
| 2344 | 2.344 |
Hint
Clear
Info
Incorrect Attempts:
CHECK
L
Hint Unavailable
Perimeter
Calculate the perimeter of a rhombus (parallelogram) with side lengths 5.5cm and 4.3cm
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Add each of the four side lengths to get the perimeter of the rhombus.
Add the 4 side lengths...
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Add each of the four side lengths to get the perimeter of the rhombus.
Calculate the side lengths of a square that has a 25 cm perimeter.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Each side of a square is equal.
Divide: 25 ÷ 4 = ...
Each side is 6.25 cm.
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Each side of a square is equal.
If 2 different squares have a total combined perimeter of 80 cm, and one of the squares has a side of 4.5 cm, calculate the side length of the other square.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Each side of a square is equal.
The perimeter of one square is 4 × 4.5cm = 18 cm.
If the total perimeter is 80 cm, then the perimeter of the other square must be:
Since the sides are all equal, divide 62 cm by 4...
Each side is 15.5 cm.
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Each side of a square is equal.
If the total perimeter is 80 cm, then the perimeter of the other square must be: Since the sides are all equal, divide 62 cm by 4... Each side is 15.5 cm.
If 2 different squares have a total combined perimeter of 82 cm, and one of the squares has a side of 11 cm, calculate the side length of the other square.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Each side of a square is equal.
The perimeter of one square is 4 × 11 cm = 44 cm.
If the total perimeter is 80 cm, then the perimeter of the other square must be:
Since the sides are all equal, divide 38 cm by 4...
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Each side of a square is equal.
If the total perimeter is 80 cm, then the perimeter of the other square must be: Since the sides are all equal, divide 38 cm by 4...
Area of Triangles
Two triangles below have the same area. The triangle on the left has a base of 8 cm, and a height of 8 cm. Determine the dimension of base of the triangle on the right.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Use the formula for the area of a triangle and compare the bases and heights
You know the area of a triangle is:
The area of triangle 1:
The area of triangle 2:
Since the areas are equal...
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Use the formula for the area of a triangle and compare the bases and heights
You know the area of a triangle is:
The area of triangle 1:
The area of triangle 2:
Since the areas are equal...
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Use the formula for the area of a triangle and compare the bases and heights
Area of Triangles
What new dimensions would be twice the area of the dimensions of the triangle below?
Solution
base = 4cm, height = 6cm
You know the area of a triangle is:
Use guess & check to find the answer choice that has twice the area... eventually check D)
Area of Parallelogram
Parallelograms are quadrilaterals that have opposite sides that are parallel and equal in length.
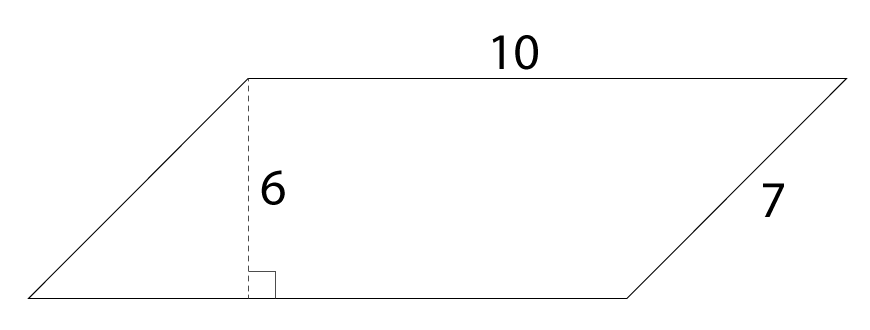
Calculate the area of the following parallelogram (diagram not to scale).
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
cm2
Hint Unavailable
Chop off the end at the dotted line and place it in the nook on the right-hand side to make a rectangle with the dimensions:
width = 10
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm2
Hint Unavailable
Chop off the end at the dotted line and place it in the nook on the right-hand side to make a rectangle with the dimensions:
width = 10
height = 6
Then calculate the area of this rectangle,
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm2
Hint Unavailable
height = 6 Then calculate the area of this rectangle,
The area of a different parallelogram is 48 cm2. If the height is 8 cm, calculate the width of one of its sides.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
You have the area and height in the formula:
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
Area of Compound Shape
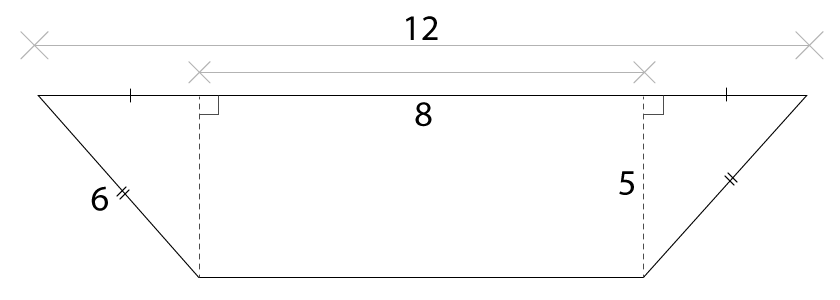
Calculate the area of the following shape using compound shapes.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
cm2
Hint Unavailable
See that this shape is made of two triangles plus one rectangle. The triangles and rectangle have:
height = 5 cm
Calculate the base lengths of the triangles.
Now that you have all the dimensions, calculate the area of each shape
Add the area of each shape together to get the total area.
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm2
Hint Unavailable
See that this shape is made of two triangles plus one rectangle. The triangles and rectangle have:
height = 5 cm
Calculate the base lengths of the triangles.
Now that you have all the dimensions, calculate the area of each shape
Add the area of each shape together to get the total area.
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm2
Hint Unavailable
Conversions Between m2 and cm2
The diagram below shows the same size squares, one is in units of meters, the other is in units of centimeters.

Calculate the area of each square.
Solution
Area of a square is the length times width. The length is the same as the width in a square. First:
Second:
True or false?
Solution
1 m2 = 10,000 cm2
This is the correct conversion.
The following table shows the conversion between square units of meters and centimeters. Fill in the blanks. Solution
| meters2 | centimeters2 |
| 0.5 m2 | _________ |
| 1 m2 | 10,000 cm2 |
| 2 m2 | 20,000 cm2 |
| 3 m2 | 30,000 cm2 |
| 4 m2 | _________ |
See the pattern, increasing by the same amount each time...
Conversions Between m2 and cm2
Given the rectangle,

Calculate the area of the rectangle, in square centimeters.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm2
Hint Unavailable
Area = Length × Width
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm2
Hint Unavailable
Convert the area of the rectangle from square centimeters into square meters.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
m2
Hint Unavailable
Know that the place value difference between m2 and cm2 is 4 places...
Convert to meters... move the decimal 4 places left.
Or, convert the lengths to meters first, and then calculate the area:
- 10 cm --> 0.1 m
- 20 cm --> 0.2 m
Hint
Clear
Info
Incorrect Attempts:
CHECK
m2
Hint Unavailable
Convert to meters... move the decimal 4 places left. Or, convert the lengths to meters first, and then calculate the area:
- 10 cm --> 0.1 m
- 20 cm --> 0.2 m
Surface Area of Rectangular and Triangular Prisms
Calculate the surface area of the rectangular prism below, including the bottom. (Diagram not drawn to scale)
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
units2
Hint Unavailable
Calculate the area of each pair of similar faces. There are 3 pairs...
Now add all 6 faces, or 3 pairs of faces,
Hint
Clear
Info
Incorrect Attempts:
CHECK
units2
Hint Unavailable
Calculate the area of each pair of similar faces. There are 3 pairs...
Now add all 6 faces, or 3 pairs of faces,
Hint
Clear
Info
Incorrect Attempts:
CHECK
units2
Hint Unavailable
A rectangular prism has the dimensions given below. Calculate the surface area, including the base.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
units2
Hint Unavailable
Calculate the area of each pair of similar faces. There are 3 pairs. It doesn't matter if you chose your length, height, and depth differently.
Now add all 6 faces, or 3 pairs of faces,
Hint
Clear
Info
Incorrect Attempts:
CHECK
units2
Hint Unavailable
If the surface area of the triangular prism below is 210 units2, determine the height 'h' of the figure. (Diagram not drawn to scale)
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
units
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
units
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
units
Hint Unavailable
Volume of Rectangular and Triangular Prisms
Calculate the volume of the following rectangular prism. (Diagram not drawn to scale)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
units3
Hint Unavailable
You can choose any combination for length, width, height
Your multiplication will be in steps, like this
Then multiply the last,
Hint
Clear
Info
Incorrect Attempts:
CHECK
units3
Hint Unavailable
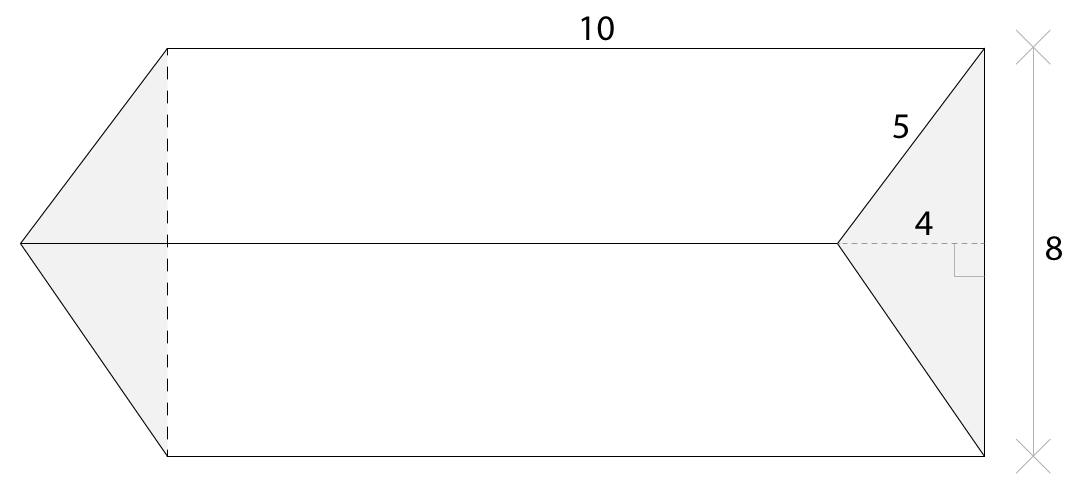
Calculate the volume of the following triangular prism. (Diagram not drawn to scale)
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
units3
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
units3
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
units3
Hint Unavailable
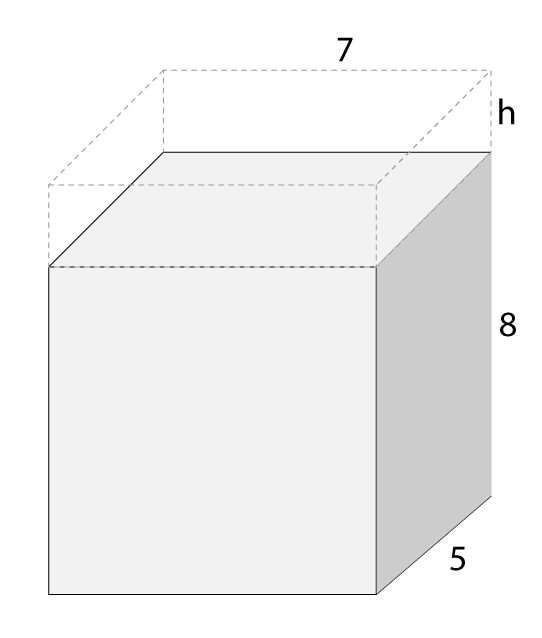
The volume of the following shaded rectangular prism is 280 units3. In order to increase the volume to 420 units3, by how much should the height 'h' be increased? (Diagram not drawn to scale)
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
units
Hint Unavailable
At this point, you are able to solve using guess and check, using a calculator, keep plugging in numbers, until eventually you find:
Therefore the height 'h' is 4 units
Hint
Clear
Info
Incorrect Attempts:
CHECK
units
Hint Unavailable
At this point, you are able to solve using guess and check, using a calculator, keep plugging in numbers, until eventually you find:
Therefore the height 'h' is 4 units
Hint
Clear
Info
Incorrect Attempts:
CHECK
units
Hint Unavailable
Geometry and Spatial Sense
Representing Angles
Which angle is greatest?
Solution
Obtuse is greater than 90˚
Classifying Triangles by Angle
Look at the differences in the angles in these triangles...

An acute triangle can have more than one acute angle in it.
Solution
True
An obtuse triangle can have more than one obtuse angle in it.
Solution
Obtuse triangles only have 1 obtuse angle.
A right angle is anything less than 90˚
Solution
A right angle is exactly 90˚
A three-sided polygon that has equal angles must be an acute triangle
Solution
True. And an acute triangle with all angles equal is called an equilateral.
What angle would you measure first to classify the triangle.
Solution

Measure the biggest angle first, if greater than 90˚ it is obtuse...
(If equal to 90˚ it is right, and if less than 90˚ it is acute)
(If equal to 90˚ it is right, and if less than 90˚ it is acute)
Classifying Triangles by Side Lengths
Look at the differences in the side lengths in these triangles, indicated by the different number of tick marks.

An isosceles triangle has all unequal side lengths.
Solution
An isosceles triangle has 2 equal side lengths.
All three side lengths of an equilateral triangle are always the same in the triangle.
Solution
True
Which is the scalene triangle?
Solution
None of the side lengths are equal in a scalene triangle.
Explain how the side lengths are shown as similar or different. [1]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
With the use of tick marks. The same number of tick marks indicates the side lengths are the same. For example, equilateral would have three single tick marks, isosceles triangle would have two single tick marks and a double, and a scalene triangle would have on of each of: single tick mark, double tick mark, and triple tick mark.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Classification Applications
Using a ruler and a protractor draw the shapes exactly, labeling the side lengths and angles.
An isosceles triangle with two 30˚ angles and a single 3.5 cm side length.
An equilateral triangle with 5cm sides.
Draw two similar triangles with the angles: 30˚, 60˚, 90˚
Challenge: see if you can draw any one of: pentagon, hexagon, or octagon...
Classifying Shapes
Which shapes are congruent?
Solution

Congruent means same size and same shape.
(The rest are similar shapes, with the same shape but different size).
(The rest are similar shapes, with the same shape but different size).
Polygons
Which one of the following is not a property of a polygon?
Solution
Polygons:
- Closed shape
- All sides are straight lines
- 2-dimensional
- Closed shape
- All sides are straight lines
- 2-dimensional
Polygons
What is a "regular polygon"? Provide at least one example. [3]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Any two of the following with same sides and angles: equilateral triangle, square, pentagon, hexagon, ...
Regular polygons have all side lengths and angles equal.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Regular polygons have all side lengths and angles equal.
Polygons
Which of the following polygons is not 4-sided?
Solution
All are 4-sided:
- Quadrilateral
- Rectangle
- Rhombus
- Square
- Trapezoid
- Parallelogram
- Kite
- Quadrilateral
- Rectangle
- Rhombus
- Square
- Trapezoid
- Parallelogram
- Kite
Quadrilateral Polygon Classification Exercise
Given the 8 terms, arrange into the categories or hierarchy - "what falls under what"...?
Solution
- Square (all sides equal, all right angles)
- Quadrilateral (4 sides)
- Rectangle (all right angles)
- Polygon (closed, 2D, straight sides)
- Rhombus (all sides equal)
- Parallelogram (2 parallel sides)
- Kite (two different pairs of equal, adjacent sides)
- Trapezoid (at least one pair of parallel sides)
 This is the general order...
This is the general order...
 Google 'em!
Google 'em!
 Google 'em!
Google 'em!
Polygon Applications
Given the pattern for the sum of the angles in the regular polygons...

Determine the sum of the angles in an octagon.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
An octagon has 8 sides...
Complete the pattern ... 540˚, 720˚, 900˚, 1080˚, ...
= 1080˚
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Complete the pattern ... 540˚, 720˚, 900˚, 1080˚, ...
= 1080˚
Calculate each 'equivalent' angle in an octagon.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
There are 8 equivalent angles and 8 equivalent sides in an octagon.
An octagon has 8 sides so divide the sum of the angles, 1080˚, by 8...
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
There are 8 equivalent angles and 8 equivalent sides in an octagon.
What is the first polygon to have each angle as an obtuse angle?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
One word, a shape.
A pentagon. See the first obtuse angle (greater than 90˚) is the pentagon with 108˚ for each angle. One up from a square with each angle at 90˚.
Hint
Clear
Info
Incorrect Attempts:
CHECK
One word, a shape.
Determine a pattern rule for the sum of the interior angles.
Solution
See that each has a first difference of 180˚...
See that,
- 3 sides is 1 × 180˚
- 4 sides is 2 × 180˚
- 5 sides is 3 × 180˚
- 6 sides is 4 ×
- ...
Determine the sum of the interior angles based on the number of sides, n
See that,
- 3 sides is 1 × 180˚
- 4 sides is 2 × 180˚
- 5 sides is 3 × 180˚
- 6 sides is 4 ×
- ...
Use a pattern rule for the sum of the interior angles, in order to calculate the sum of the interior angle of a regular decagon (with 10 sides).
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
A dodecagon has 10 equal sides and 10 equal interior angles
10 sides, so n = 10...
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
A dodecagon has 10 equal sides and 10 equal interior angles
Patterning and Algebra
Determine the Pattern Rule
Given the following pattern, determine the pattern rule.
Solution
Video
5.5, 11, 16.5, 22, 27.5, 33...
Determine the pattern rule quickly: +5.5


Pattern Rules: Term Number
What is the term number of 60 in the following pattern?
Solution
Video
15, 30, 45, 60, 75, 90...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Term numbers start at 1
60 is the 4th term in the pattern, so the term number is 4.

Hint
Clear
Info
Incorrect Attempts:
CHECK
Term numbers start at 1

The 5th term in the following pattern is 54.
Solution
Video
9, 18, 27, ...
Determine the pattern rule first: +9. Then find the 5th term.
 5th term is 45.
5th term is 45.
 5th term is 45.
5th term is 45.
Patterning: Filling in Tables
Complete the following table by finding the missing numbers for the number and cost of tickets.
Solution
Video
Hint
Clear
Info
Number of Tickets Cost
1 $18.00
3 $23.00
5 $28.00
7 $33.00
9
$43.00
Incorrect Attempts:
CHECK
Follow the pattern
Find the pattern rule for the number of tickets, and the pattern rule for the cost.
Number of tickets: +2
Cost: +5.
 The missing numbers are 11 tickets, and $38.00
The missing numbers are 11 tickets, and $38.00
Hint
Clear
Info
| Number of Tickets | Cost |
| 1 | $18.00 |
| 3 | $23.00 |
| 5 | $28.00 |
| 7 | $33.00 |
| 9 | |
| $43.00 |
Incorrect Attempts:
CHECK
Follow the pattern
Number of tickets: +2
Cost: +5.
 The missing numbers are 11 tickets, and $38.00
The missing numbers are 11 tickets, and $38.00
Patterning
Start with 3 and add 10 to each term to get the next term. Determine the term number when the term is 53
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Start with 3, and then use the pattern rule of 10 up to 53...
 The term number is 6.
The term number is 6.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
 The term number is 6.
The term number is 6.
Representing Pattern Rules from Words
Make a table of values and a graph of the coordinates for the following pattern rule. Let 'x' be the term number, and let 'y' be the term. Solution Start with 2, then add one to each term and double it to get the next term.
| x | y |
| 1 | 2 |
| 2 | __ |
| 3 | __ |
| 4 | __ |
| 5 | __ |
| x | y |
| 1 | 2 |
| 2 | 6 |
| 3 | 14 |
| 4 | 30 |
| 5 | 62 |
Patterning with Multiplication and Division
Determine the pattern rule for the following pattern, without the use of a calculator.
Solution
Video
3, 12, 48, 192, 768...
Find out what it multiplies by each time: × 4.
 The pattern rule is multiply by 4...
The pattern rule is multiply by 4...
 The pattern rule is multiply by 4...
The pattern rule is multiply by 4...
Equations
Which of the following equation statements is incorrect?
Solution
Video
Do a quick check by simplifying some of the ones that look funny, try d)...
Variables are Numbers Too
Substitute the given numbers in the equation and multiply, like this for example:
When: a = 3, b = 4, c = 5
Solution
2 × a × b × c
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
When: x = 2, y = 2, z = 3
Solution
5xyz
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solving Simple Equations with One Variable Using Guess and Check
The missing number represented by the in the following equation is:
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Identifying Variables and Constants
In the following equation for the area of a triangle, the is called a(n)
Solution
Video


Solving Simple Equations with One Variable Using Guess and Check (A, S)
Find the missing numbers using guess and check. Show your work and simplify line-by-line.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Solving Simple Equations with One Variable Using Guess and Check (A, S, M)
Find the missing numbers using guess and check. Show your work and simplify line-by-line.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
*
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Solve with guess and check... 1, 2, 3, 4, 5, 6!
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Solving Simple Equations with One Variable Using Guess and Check (D)
Find the missing numbers using guess and check. Show your work and simplify line-by-line.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
With guess and check...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
With guess and check...
Or with more advanced rearrangement (Not required)...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
With guess and check...
Or with more advanced rearrangement (Not required)...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
With guess and check...
Or with more advanced rearrangement (Not required)...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check
Practice with Variables
The following expression correctly describes: "eight more than a number (n)".
Solution
n + 8
True
Determine the correct expression for the following.
Solution
Three less than a number (n)
"Three less than a number" means subtract (take away) 3 from your number, n.
Determine the correct expression for representing the following.
Solution
Seven times more than which number is thirty-five
Hint
Clear
Info
= 7 ×
Incorrect Attempts:
CHECK
Hint Unavailable
7 × ___ = 35
35 = 7 × ___
Hint
Clear
Info
= 7 ×
Incorrect Attempts:
CHECK
Hint Unavailable
35 = 7 × ___
Are all of the following are equal?
Solution
Video
2 × n = 2n = (2)(n)
Yes these are all the same. They all mean multiply 2 × n.


Solve for the value of 'n'.
Solution
3n = 36
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check, or division
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check, or division
Solve.
Solution
4(3)(n) = 60
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check, or division
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check, or division
Variables with Factors of 10
Solve for each of the unknown variables.
(10)(21.5) = n
Solution
Video
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check, multiplication, or division
Multiplying by 10 makes the number bigger.
Move the decimal place 1 to the right (because there is 1 zero in 10).
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check, multiplication, or division
(100)(0.0012) = r
Solution
Video
r =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check, multiplication, or division
Multiplying by 100 makes the number bigger.
Move the decimal place 2 places to the right (because there are 2 zeros in 100).
r =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check, multiplication, or division
345.1n = 3451
Solution
Video
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check, multiplication, or division
You can see that the number got bigger by a factor of 10, so the decimal must have been multiplied by 10.
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check, multiplication, or division
3 × n × 2 × 2 = 60
Solution
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check, multiplication, or division
Multiply the numbers together
See it works,
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check, multiplication, or division
10n = 22.22
Solution
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check, multiplication, or division
The variable (n) should be a factor of 10 lower than 22.22, so move the decimal place once to the left.
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check, multiplication, or division
100n = 1.234
Solution
Video
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check, multiplication, or division
Multiplying by 100 moves the decimal place 2 to the right, which gave us the bigger number, 1.234
So the number had to be 2 decimal places smaller → move the decimal 2 to the left.
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check, multiplication, or division
So the number had to be 2 decimal places smaller → move the decimal 2 to the left.
145.6n = 0.01456
Solution
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check, multiplication, or division
The number got smaller, so it was multiplied by a decimal.
The decimal place moved 3 times, so the number was 0.0001
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use guess and check, multiplication, or division
Variables
Solve for the variable.
Solution
200n = 100
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(Also accept 0.5)
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Small Word Problem With Algebra
You know that the perimeter is calculated with the equation:
P = 2L + 2WIf the length is 3cm and the width is 4cm, calculate the perimeter (using algebra).
Solution
P =
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
P =
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
If the perimeter is 30cm, and the length is 10cm, calculate the width (using algebra).
Solution
W =
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
The width is 10cm!
W =
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
Algebraic Expressions
Packs of gum cost $4.00 each, and packs of batteries cost $5.99 each.
Determine an expression for the cost of 2 packs of gum and 'n' amount of battery packs.
Solution
Also accept answers with different arrangements:
- 5.99n + 8
- (5.99)(n) + 8
- 8 + n(5.99)
- 8 + n × 5.99
- 8 + 5.99(n)
- ...
- 5.99n + 8
- (5.99)(n) + 8
- 8 + n(5.99)
- 8 + n × 5.99
- 8 + 5.99(n)
- ...
Data Management and Probability
Trends
Describe the trend.
Solution

The 'overall' trend is increasing.
Which of the following trends would increase overall?
Solution
World population is increasing constantly.
Scale and Appearance
Describe how changing the scale of a graph can alter the appearance in favor of the creator of the graph. [2]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Changing the scale of the axis on the left (y-axis) can make the graph appear smaller, or larger.

Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable


