GRADE
12
Chemistry SCH4U
This course enables students to deepen their understanding of chemistry through the study of organic chemistry, energy changes and rates of reaction, chemical equilibrium, atomic and molecular structure, and electrochemistry. Students will further develop problem-solving and laboratory skills as they investigate chemical processes, at the same time refining their ability to communicate scientific information. Emphasis will be placed on the importance of chemistry in daily life, and on evaluating the impact of chemical technology on the environment. Prerequisite: Grade 11 Chemistry SCH3U
TABLE OF CONTENTS
Recall of Basic Chemistry
Polarity of Bonds
Which of the following bonds is most polar?
Solution
Polarity is directly proportional to the difference in electronegativity
O-H
Oxygen electronegativity = 3.5, Hydrogen electronegativity = 2.1
Electronegativity Difference: 3.5 - 2.1 = 1.4
Na-F
Sodium electronegativity = 0.9, Fluorine electronegativity = 4.0
Electronegativity Difference: 4.0 - 0.9 = 3.1
The highest polarity is between the metal and non-metal with the greatest electronegativity difference.
H-Cl
Hydrogen electronegativity = 2.1, Chlorine electronegativity = 3.0
Electronegativity Difference: 3.0 - 2.1 = 0.9
Mg-Br
Magnesium electronegativity = 1.2, Bromine electronegativity = 2.8
Electronegativity Difference: 2.8 - 1.2 = 1.6
B-F
Boron electronegativity = 2.0, Fluorine electronegativity = 4.0
Electronegativity Difference: 4.0 - 2.0 = 2.0
O-H
Oxygen electronegativity = 3.5, Hydrogen electronegativity = 2.1
Electronegativity Difference: 3.5 - 2.1 = 1.4
Na-F
Sodium electronegativity = 0.9, Fluorine electronegativity = 4.0
Electronegativity Difference: 4.0 - 0.9 = 3.1
The highest polarity is between the metal and non-metal with the greatest electronegativity difference.
H-Cl
Hydrogen electronegativity = 2.1, Chlorine electronegativity = 3.0
Electronegativity Difference: 3.0 - 2.1 = 0.9
Mg-Br
Magnesium electronegativity = 1.2, Bromine electronegativity = 2.8
Electronegativity Difference: 2.8 - 1.2 = 1.6
B-F
Boron electronegativity = 2.0, Fluorine electronegativity = 4.0
Electronegativity Difference: 4.0 - 2.0 = 2.0
Types of Bonding
Answer the following question on the different types of bonding.
What is an ionic bond? [3]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Ionic bonds form when electrons are transferred from the positive cation to the negative anion. These oppositely charged atoms are attracted (electrostatically).
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Describe what makes a covalent bond non-polar. [3]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
- Low electronegativity difference between the atoms,
- ...results in relatively equal sharing of the bonding electrons,
- ...results in negligible dipole moment (polarity).
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
- Low electronegativity difference between the atoms,
- ...results in relatively equal sharing of the bonding electrons,
- ...results in negligible dipole moment (polarity).
Units: Mass and Volume
1.0 kg equals:
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
g
Hint Unavailable
1.0 kg = 1,000 g
Hint
Clear
Info
Incorrect Attempts:
CHECK
g
Hint Unavailable
1 mL equals:
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm3
Hint Unavailable
1 mL = 1 cm3.
(1,000 L = 1 m3)
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm3
Hint Unavailable
(1,000 L = 1 m3)
Lewis Structures
Draw the lewis structure for NO31-
Draw a lewis structure for CH4
Naming Multivalent Metals
Iron has two different charge states, iron(II) and iron(III). When referring to the charges on an element, the name can be ferrous, in which the suffix -ous refers to:
Solution
-ous is a lower charged state, whereas -ic is a higher charged state. Be careful, "-ous" does not always refer to a +2 charge. It is a relative term, and the magnitude depends on the element.
Naming Compounds
Name the hydrate: CuSO4·5 H2O
Solution
Copper is multivalent, therefore name using the stock naming system to indicate the charge with a roman numeral...
The amount of waters is named with the prefix system... 5 is penta...
copper(II) sulfate pentahydrate
The amount of waters is named with the prefix system... 5 is penta...
copper(II) sulfate pentahydrate
Periodic Trends Review
On the periodic table, atomic radius decreases
Solution
Up a group (because less energy levels), and left-to-right across a period (because higher nuclear/valence charge).
Classifying Types of Reactions
Which of the following is a combustion reaction?
Solution
Types of Combustion Reactions
Carbon + Oxygen → Water + Carbon Dioxide
Non-metal + Oxygen → Non-metal Oxide
Metal + Oxygen → Metal Oxide
Carbon + Oxygen → Water + Carbon Dioxide
Non-metal + Oxygen → Non-metal Oxide
Metal + Oxygen → Metal Oxide
The following reaction is a...
Solution
In this single displacement reaction, the non-metal replaces the non-metal.
Molecular Weight
Calculate the molecular weight of ammonium sulfate in the following reaction, rounded to the nearest whole number.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
g/mol
Hint Unavailable
Ammonium sulfate, (NH4)2SO4:
N × 2
H × 8
S × 1
O × 4
= 132 g/mol
Hint
Clear
Info
Incorrect Attempts:
CHECK
g/mol
Hint Unavailable
N × 2
H × 8
S × 1
O × 4
= 132 g/mol
Review Chemical Formulas: Criss-Cross Method
The chemical formula of aluminum chloride is:
Solution
Balance the charges, Al3+ & Cl1-...
AlCl3
AlCl3
Balancing Chemical Equations
Write a balanced chemical equation for the following reaction:
Solution
Iron + Copper(II) Sulfate → Copper + Iron(II) Sulfate
Hint
Clear
Info
+
→
+
Incorrect Attempts:
CHECK
Hint Unavailable
Fe(s) + CuSO4 (aq) → Cu(s) + FeSO4 (aq)
Hint
Clear
Info
+
→
+
Incorrect Attempts:
CHECK
Hint Unavailable
Reactions
Solid aluminum reacts with aqueous hydrochloric acid in a single displacement reaction. Given these reactants, complete the reaction equation and balance it.
Solution
Hint
Clear
Info
+
→
+
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
+
→
+
Incorrect Attempts:
CHECK
Hint Unavailable
Mass and Moles
Determine the molar mass of gold(III) trinitrate
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
g/mol
Hint Unavailable
gold(III) trinitrate = Au(NO3)3:
Au × 1
N × 3
O × 9
= 501 g/mol
Hint
Clear
Info
Incorrect Attempts:
CHECK
g/mol
Hint Unavailable
Au × 1
N × 3
O × 9
= 501 g/mol
How many moles are in 39.0 g of NaCl?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
mol
Hint Unavailable
First calculate the molar mass of NaCl is 58.44 g/mol...
Hint
Clear
Info
Incorrect Attempts:
CHECK
mol
Hint Unavailable
Mass and Moles
Calculate the unknown quantities in each of the following questions.
How many moles of oxygen atoms are in 3.0 mol of aluminum oxide?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
mols
Hint Unavailable
Al2O3 has 3 oxygen atoms per molecule. Given 3 mol of the molecules there are 3 x 3 = 9 moles of oxygen atoms.
Hint
Clear
Info
Incorrect Attempts:
CHECK
mols
Hint Unavailable
Determine the mass of 4.5 mol of H2CO3
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
g
Hint Unavailable
= 279 g
Hint
Clear
Info
Incorrect Attempts:
CHECK
g
Hint Unavailable
Determine how many molecules are in 10.0 g of NaCl given Avogadro's constant: 6.02 × 1023 particles/mol.
Solution
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
molecules
Hint Unavailable
= 1.03 × 1023 molecules
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
molecules
Hint Unavailable
Empirical and Molecular Formula
A molecule contains 85.7% carbon and 14.3% hydrogen.
Determine the empirical formula.
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
CH2 (Solution not shown)
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
If the molar mass of the compound is 56 g/mol, determine the molecular formula.
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
C4H8 (Solution not shown)
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
Determining the Limiting Reagent
Given 50 slices of bread, 24 leaves of lettuce, and 84 slices of cheese, determine the limiting ingredient in the following recipe:
Solution
2 Bread + 1 Lettuce + 3 Cheese → 1 Sandwich
Bread
Can make 50/2 = 25 sandwiches with the starting amount.
Lettuce
Can make 24/1 = 24 sandwiches with the starting amount.
Cheese
Can make 84/3 = 28 sandwiches with the starting amount.
Therefore the lettuce is the limiting ingredient.
Can make 50/2 = 25 sandwiches with the starting amount.
Lettuce
Can make 24/1 = 24 sandwiches with the starting amount.
Cheese
Can make 84/3 = 28 sandwiches with the starting amount.
Therefore the lettuce is the limiting ingredient.
In the imaginary reaction below, 10 mol of AB, 15 mol of CD, 6 mol of EF, and 16.5 mol of G react, which reactant is limiting?
Solution
4AB + 5CD + EF + 3G → 2HI + J + 8K
The lowest numer is limiting.
AB: 10/4 = 2.5
CD: 15/5 = 3.0
EF: 6/1 = 6
G: 16.5/3 = 5.5
Therefore AB is the limiting reactant
AB: 10/4 = 2.5
CD: 15/5 = 3.0
EF: 6/1 = 6
G: 16.5/3 = 5.5
Therefore AB is the limiting reactant
Determining the Limiting Reagent
Given 100g of HCl and 100g of CaCO3, which of the following will be consumed first as the limiting reagent (reactant)? (Careful: don't forget to balance your equation first.)
Solution
Don't forget to balance first.
Second: convert mass to moles.
Third: Divide moles by the stoichiometric coefficient - the lower number is from our limiting reagent.
Since CaCO3 has a lower ratio, then it is the limiting reagent.
Third: Divide moles by the stoichiometric coefficient - the lower number is from our limiting reagent.
Since CaCO3 has a lower ratio, then it is the limiting reagent.
Stoichiometry: Theoretical Yield
If O2(g) is in excess, and 42.0g of C2H4(g) is consumed in the following reaction, determine the theoretical yield of CO2(g).
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
g
Hint Unavailable
Since there are only two reactants and one of them is in excess, then the theoretical yield has to be based on the only other reactant → C2H4(g).
1st, convert mass to moles:
2nd, use the stoichiometric ratio of C2H4 to CO2.
3rd, convert moles to mass:
Hint
Clear
Info
Incorrect Attempts:
CHECK
g
Hint Unavailable
1st, convert mass to moles: 2nd, use the stoichiometric ratio of C2H4 to CO2. 3rd, convert moles to mass:
Percent Yield
If 50.0 g of K2S reacts with excess zinc chloride to produce 40.1 g of zinc sulfide, determine the percent yield of the precipitate.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
%
Hint Unavailable
Since there are only two reactants and one of them is in excess, then the theoretical yield has to be based on the only other reactant → K2S.
1st, convert mass to moles:
2nd, use the stoichiometric ratio of K2S to ZnS.
3rd, convert moles to mass:
4th, calculate percent yield
Hint
Clear
Info
Incorrect Attempts:
CHECK
%
Hint Unavailable
1st, convert mass to moles: 2nd, use the stoichiometric ratio of K2S to ZnS. 3rd, convert moles to mass: 4th, calculate percent yield
Units: Solutions
In solutions chemistry, the unit 'M' refers to
Solution
Capital 'M' stands for molarity, which is the unit of concentration. This is the same as mol/L.
Calculating Molarity
Determine the molarity (molar concentration) of 1.0 mol NaCl dissolved in 250 mL of water.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
mol/L
Hint Unavailable
Although 1 mol NaCl dissociates into 2 mols of ions: Na+ + Cl-, the molar concentration uses the mols of the solute, or compound instead of the total ion equivalent.
Hint
Clear
Info
Incorrect Attempts:
CHECK
mol/L
Hint Unavailable
The concentration of chloride anions (Cl-) in 1.0 mol of MgCl2, dissolved in 1.0 L of water is 2 mol/L
Solution
MgCl2 dissociates into 2 chloride (Cl-) ions:
1.0 mol of MgCl2 dissolved in 1.0L of water = 1 mol/L MgCl2.
Since there are every 1 MgCl2 forms 2 Cl- ions, then the molarity of chloride anions (Cl-)
= 2(1 mol/L)
= 2 mol/L
Since there are every 1 MgCl2 forms 2 Cl- ions, then the molarity of chloride anions (Cl-) = 2(1 mol/L)
= 2 mol/L
Calculating Molarity
Determine the mass of potassium nitrate (KNO3) required to make 1,250 mL of a 0.50 M solution.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
g
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
g
Hint Unavailable
120 mL of 4.5 mol/L potassium fluoride (KF) is added to 100 mL of water. Determine the new molarity of the solution.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
mol/L
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
mol/L
Hint Unavailable
25 mL of a 4 mol/L solution is used to prepare a 2.5 mol/L solution. Determine the final volume in milliliters.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
mL
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
mL
Hint Unavailable
Net Ionic Equation
Determine the net ionic equation for the reaction below. Show your work in your own notes.
Solution
Separate the ions of all soluble compounds (leaving the solid, liquid, and gases).
Cancel ions on the left and right side, leaving:
Cancel ions on the left and right side, leaving:
Acids and Bases
Which of the following is a strong acid?
Solution
This year you should memorize the 6 most common:
6 Most Common Strong Acids
HCl HBr HI HNO3 H2SO4 HClO4
| 6 Most Common Strong Acids | |||||||||||||||||
| HCl | HBr | HI | HNO3 | H2SO4 | HClO4 | ||||||||||||
Which of the following is a monoprotic acid?
Solution
"Monoprotic" means there is 1 (mono) acidic proton in the molecule.
Of the answer choices, acetic acid CH3COOH has only one acidic proton and forms the acetate ion plus one proton: CH3COO-1 + H+
Of the answer choices, acetic acid CH3COOH has only one acidic proton and forms the acetate ion plus one proton: CH3COO-1 + H+
Conjugate Pair of Acids and Bases
Which of the following is a conjugate acid-base pair?
Solution
The carbonic acid H2CO3 dissociates into the bicarbonate anion, which forms a salt with the available sodium ions, as sodium bicarbonate: NaHCO3
Solutions of Acids and Bases: Monoprotic Neutralization
A 3.33 L sample of 8.88 mol/L nitric acid (HNO3) is used to neutralize what volume of 4.44 mol/L potassium hydroxide (KOH)?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
L
Hint Unavailable
Neutralization equation:
Hint
Clear
Info
Incorrect Attempts:
CHECK
L
Hint Unavailable
Thermochemistry: Endothermic and Exothermic
A reaction that causes the temperature of the system to decrease from 12.˚C to 5.4˚C is endothermic.
Solution
Endothermic reactions absorb heat energy, causing the temperature of the system to decrease. Exothermic reactions release heat energy, causing the temperature of the system to increase.
Converting Kelvin and Celsius
Convert 273K to Celsius:
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
˚C
Hint Unavailable
Celsius = Kelvin - 273
Kelvin = 273K - 273
= 0˚C
Hint
Clear
Info
Incorrect Attempts:
CHECK
˚C
Hint Unavailable
Kelvin = 273K - 273
= 0˚C
Definition of Specific Heat
Specific heat is defined as
Solution
Specific heat is
The energy required to raise the temperature of one gram by 1˚C
The energy required to raise the temperature of one gram by 1˚C
Specific Heat
12 kJ of energy is added to water causing the temperature to increase from 296K to 343K. If the specific heat capacity of water is 4.18 J/(g·˚C) determine the mass of water.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
g
Hint Unavailable
q = mc(T2 - T1)
Make sure to use Joules and not Kilojoules in the equation...
Change in temperature can use either Kelvin or ˚C because the magnitude of the change is the same for both.
Hint
Clear
Info
Incorrect Attempts:
CHECK
g
Hint Unavailable
Make sure to use Joules and not Kilojoules in the equation...
Change in temperature can use either Kelvin or ˚C because the magnitude of the change is the same for both.
Gas Laws
Which of the following is Charles' Law?
Solution
Charles' Law:
Gay-Lussac's Law:
Avogadro's Law:
Boyle's Law: P1V1 = P2V2
Ideal Gas Law: PV = nRT
Gay-Lussac's Law:
Avogadro's Law:
Boyle's Law: P1V1 = P2V2
Ideal Gas Law: PV = nRT
Dalton's Law of Partial Pressure
If 12 kPa of O2 gas is mixed with the following gases in a 20 L container, determine the total pressure if they do not react: 20 kPa CO2, and 30 kPa N2.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
kPa
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
kPa
Hint Unavailable
Ideal Gas Law
Determine the temperature of 10.0 g of carbon dioxide gas (CO2) in a 500mL container at 1.5 atm. (R = 8.31 kPa·L/mol·K)
Solution
T =
Hint
Clear
Info
Incorrect Attempts:
CHECK
K
Hint Unavailable
First convert all units to those used in 'R': kPa·L/mol·K
500mL = 0.5L
1.5atm =
Convert 10.0g of CO2 to moles:
Plug into equation to solve for T.
T =
Hint
Clear
Info
Incorrect Attempts:
CHECK
K
Hint Unavailable
500mL = 0.5L
1.5atm =
Convert 10.0g of CO2 to moles:
Plug into equation to solve for T.
Molar Volume
At STP (0˚C and 101.3 kPa), the molar volume of a gas is 22.4 mol/L. Determine the volume that 50.0 g of fluorine gas occupies.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
L
Hint Unavailable
Convert to mol,
Use molar volume at STP:
Hint
Clear
Info
Incorrect Attempts:
CHECK
L
Hint Unavailable
Stoichiometry with Gases
100 g of nitrogen gas combines with excess hydrogen in the following synthesis reaction at (0˚C, 101.3 kPa, 22.4 mol/L), determine the mass of ammonia produced.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
g
Hint Unavailable
First: Convert mass to moles
Second: Use the stoichiometric ratio
Third: Convert moles to mass
Hint
Clear
Info
Incorrect Attempts:
CHECK
g
Hint Unavailable
Flashcards: Basic Review
| How many electron are in a Chlorine ion if there are 17 protons? |
| The ion Cl-1 has a total of 18 electrons. |
| How many neutrons are in a Carbon-14 atom if there are 6 protons? |
| 8 neutrons |
| What is a group in a periodic table? |
| A vertical column |
| What is a period in a periodic table? |
| A horizontal row |
| What are the group numbers of alkali metals, alkaline metals, halogens, and noble gases? |
| 1, 2, 17 (7A), and 18 (8A) |
| What is an anion and a cation? |
| Anion is a negative ion, cation is a positive ion |
| Do transition metals within the same group show the same chemical properties? |
| No transition metals do not, but all other elements within certain groups do show similar chemical properties within the group. |
| How is the periodic table organized? |
| By number of protons (atomic number). |
| What is the periodic trend in ionization energy? |
| Ionization increases left→right across a period and bottom→top up a group. This is due to electrons being held more tightly by the nucleus. |
| Is the second ionization energy always higher than the first ionization energy, even for group 2 elements? |
| Yes |
| What is the periodic trend in electron affinity? |
| The trend is the same as ionization energy, electron affinity increases left→right across a period and bottom→top up a group. Electron affinity is the energy released when an atom gains an electron. |
| What is the periodic trend in atomic radius of neutral atoms of elements? |
| This is the trend opposite to all others. Atomic radius decreases left→right across a period and bottom→top up a group. (This is because the number of energy levels decreases bottom→top up a group and the valence and nuclear charge attractions increase left→right across a period.) |
| What is the periodic trend in electronegativity? |
| The trend is the same as ionization energy, electronegativity increases left→right across a period and bottom→top up a group. |
| What classification of elements is the following? Boron, Silicon, Germanium, Arsenic, Antimony, and Tellurium |
| Metalloids |
| What are some of the physical properties of metals versus nonmetals? |
| Metals are malleable solids, good conductors of heat and electricity, shiny. Nonmetals are brittle solids, poor conductors of heat and electricity, dull. |
| Describe the 2 main intra-molecular bonds |
| Covalent bonds share electrons while ionic bonds involve the transfer of electrons. |
Organic Chemistry
Organic
What is considered the main requirement for a molecule to be classified as organic?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Must have carbon-carbon, or carbon-hydrogen bonds.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Which of the following molecules is considered organic ?
Solution
Only molecules with carbon-carbon, or carbon-hydrogen bonds are considered organic. The following are inorganic molecules: CO2, CO, CN-, H2CO3, CO32-, C22-, etc...
Naming Branched Alkanes
Take note of the 5-ish steps to naming an organic molecule. Use this in your journey ahead...
Solution
1) Determine the longest, continuous carbon-chain as the root.
2) Number the chain with the lowest number at the highest priority functional group, and with the lowest combination (sum) of numbers for the side group substituents.
3) Name the priority/parent functional group, and add ending/suffix if applicable. Name the side groups and add prefixes, if any, and place in alphabetical order with the assigned carbon number of each substituent. (Prefixes do not count for alphabetical order: di, tri, tetra).
4) If two of the same substituents exist then number each and include the prefix (di, tri, tetra) in-front of the substituent name.
5) Combine all substituents and the suffix for the carbon chain, including any suffix for alkenes or alkynes.
2) Number the chain with the lowest number at the highest priority functional group, and with the lowest combination (sum) of numbers for the side group substituents.
3) Name the priority/parent functional group, and add ending/suffix if applicable. Name the side groups and add prefixes, if any, and place in alphabetical order with the assigned carbon number of each substituent. (Prefixes do not count for alphabetical order: di, tri, tetra).
4) If two of the same substituents exist then number each and include the prefix (di, tri, tetra) in-front of the substituent name.
5) Combine all substituents and the suffix for the carbon chain, including any suffix for alkenes or alkynes.
Naming Branched Alkanes
The name of this molecule is
Solution
Video
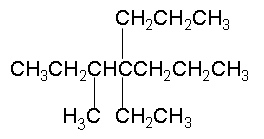
The lowest possible combination of numbers for the substituents is obtained by starting the numbering from the leftmost side of the molecule.
This results in 3, 4, 4 (rather than 4, 4, 5).
Also remember to list the substituents in alphabetical order (e → m → p).
This results in 3, 4, 4 (rather than 4, 4, 5).
Also remember to list the substituents in alphabetical order (e → m → p).
Halogen side groups have a greater priority than alkyl side groups. Therefore start numbering the parent backbone chain from the side closer to the halide group.
Solution
Halogen and alkyl side groups have an equal priority. Therefore just start numbering the backbone to give the lowest combination of numbers on side groups.
When naming a molecule with many different side groups, the side groups are listed alphabetically according to the root name of the side group and the prefixes.
Solution
When ordering the side groups in the name, the prefixes (mono, di, tri, tetra...) are not considered in the alphabetic ordering.
- Exception: only the prefixes cyclo-, iso-, and neo are considered for alphabetical order.
- Exception: only the prefixes cyclo-, iso-, and neo are considered for alphabetical order.
Naming Alkanes, Alkenes, Alkynes, and Alkyl Halides
Name the following hydrocarbons.
With lots of branching.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
3-ethyl-2-methyl-4-propylnonane
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
3-ethyl-2-methyl-4-propylnonane
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
With multiple double bonds.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
2,4-dimethylpent-1,5-diene
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
2,4-dimethylpent-1,5-diene
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
With branching, alkyne, and a halide.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
3-chloro-3-iodobut-1-yne
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
3-chloro-3-iodobut-1-yne
(Start numbering from the alkyne side)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(Start numbering from the alkyne side)
With equal numbers of carbon in the chain and cyclic.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The cyclic group takes priority as the backbone when the cyclic carbon number is 'greater than or equal to' the number of carbons in the straight chain.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The cyclic group takes priority as the backbone when the cyclic carbon number is 'greater than or equal to' the number of carbons in the straight chain.
The straight chain has 4C and the cyclic has 4C, so the backbone is cyclobutane.
sec-butyl cyclobutane
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The straight chain has 4C and the cyclic has 4C, so the backbone is cyclobutane.
sec-butyl cyclobutane
With a longer straight chain than the cyclic group.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The 8C straight chain takes priority over the 3C cyclic group...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The 8C straight chain takes priority over the 3C cyclic group...
4-cyclopropyl-octane
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
4-cyclopropyl-octane
With more carbons in the cyclic group.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The longest continuous carbon structure will take priority as the backbone... this is the 6C cyclohexane...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The longest continuous carbon structure will take priority as the backbone... this is the 6C cyclohexane...
When listing alphabetically, 'cyclo-' counts!
1-cyclobutyl-4-ethyl-cyclohexane
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
When listing alphabetically, 'cyclo-' counts!
1-cyclobutyl-4-ethyl-cyclohexane
With branching on cyclic.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
3-chloro-1-ethyl-6-methylcyclohexene
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
3-chloro-1-ethyl-6-methylcyclohexene
(Priority: Alkene > Alkyl > Halogen)
(Lowest numbering combination, must fully encompass double bond at start: 3-1-6 < 2-3-6)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(Priority: Alkene > Alkyl > Halogen)
(Lowest numbering combination, must fully encompass double bond at start: 3-1-6 < 2-3-6)
Structural Formula
Draw the structural formula for 4,4-dibromo-2-iodo-5,5-dimethyloctane.
Solution
Video
Remember in naming that the prefix does not count for alphabetical order (except for iso). The halogen and alkyl side groups have equal priority, so just make the lowest combination of numbers.
Start numbering from the side that will make the lowest combination of numbers of the side groups, from the left-hand side: 2, 4, 4, 5, 5. (Numbering from the right-hand side would be: 4, 4, 5, 5, 7)
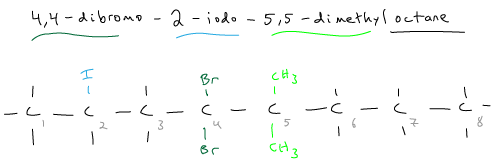
Start numbering from the side that will make the lowest combination of numbers of the side groups, from the left-hand side: 2, 4, 4, 5, 5. (Numbering from the right-hand side would be: 4, 4, 5, 5, 7)

Unsaturated Hydrocarbons
What does unsaturated mean? [1]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Unsaturated means it has double or triple bonds
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Physical Properties of Hydrocarbons
At room temperature, propane is a gas, octane is a liquid, and a 20-carbon hydrocarbon is a solid.
Solution
Melting point and boiling point of hydrocarbons increase with molecular weight. C1-C4 is gas, C5-C12 is liquid, and C20+ is solid.
Order the following hydrocarbons in order of decreasing boiling point from top to bottom.
Solution
Pentane
Decane
Ethane
Hexane
The 2 factors that affect boiling point: molecular weight, and intermolecular forces.
When the functional groups are the same, then the molecular weight is what determines the boiling point. Higher molecular weights have higher boiling points, and visa versa.
Pentane
Decane
Ethane
Hexane
When the functional groups are the same, then the molecular weight is what determines the boiling point. Higher molecular weights have higher boiling points, and visa versa.
Butane has a lower boiling point than 2-methylpropane.
Solution
Comparing the molecular weights first, they are roughly the same so we look at the branching next. Butane has a higher boiling point than 2-methylpropane because it packs more tightly. Branched molecules of a similar molecular weight will have a lower boiling point.
Choose the most correct statement.
Solution
- Butane has a lower solubility in water than Methane
- Ethane is slightly soluble in water (over 50mg/L at standard conditions)
- Hydrocarbons with less than 3 carbons have a low solubility in water -- yes, the are slightly soluble in water.
- Low-carbon compounds (1-3) carbons are slightly soluble in water and solubility decreases as carbon number of the hydrocarbon increases.
- Butane has a lower solubility in water than Methane
- Ethane is slightly soluble in water (over 50mg/L at standard conditions)
- Hydrocarbons with less than 3 carbons have a low solubility in water -- yes, the are slightly soluble in water.
- Low-carbon compounds (1-3) carbons are slightly soluble in water and solubility decreases as carbon number of the hydrocarbon increases.
Addition Reactions of Acid Halides with Alkenes (Markovnikov)
2-methyl-1-butene reacts with HBr to form what major product?
Solution
Video
Markovnikov Addition
In the major product, the hydrogen (H) atom attaches to the carbon with fewer alkyl (C) substituents, or the larger number of hydrogen atoms. The halide (X) group becomes attached to the carbon with more alkyl substituents.
The bromine attaches to the 3˚ carbon and the hydrogen attaches to the 1˚ carbon across the double bond.
The major product is 2-bromo-2-methylbutane (and the minor product is 1-bromo-2-methylbutane).
In the major product, the hydrogen (H) atom attaches to the carbon with fewer alkyl (C) substituents, or the larger number of hydrogen atoms. The halide (X) group becomes attached to the carbon with more alkyl substituents.
The bromine attaches to the 3˚ carbon and the hydrogen attaches to the 1˚ carbon across the double bond. The major product is 2-bromo-2-methylbutane (and the minor product is 1-bromo-2-methylbutane).
What reaction type results in the major product of the reaction shown below?
Solution

Markovnikov Addition in Hydrohalogenation
In the major product, the hydrogen (H) atom attaches to the carbon with fewer alkyl (C) substituents, or the larger number of hydrogen atoms. The halide (X) group becomes attached to the carbon with more alkyl substituents.
In the major product, the hydrogen (H) atom attaches to the carbon with fewer alkyl (C) substituents, or the larger number of hydrogen atoms. The halide (X) group becomes attached to the carbon with more alkyl substituents.
Adding water to which of the following will make an equal mixture of two different products?
Solution
Video
Markovnikov Addition
In the major product, the hydrogen (H) atom attaches to the carbon with fewer alkyl (C) substituents, or the larger number of hydrogen atoms. The hydroxide (OH) group becomes attached to the carbon with more alkyl substituents.
2-methyl-2-butene ✘
- Major product will form with -OH group attached to carbon 2, forming 2-methyl-2-butanol
- OH will add to the 3˚ carbon more than the 2˚ carbon
- (Minor product formed is 3-methyl-2-butanol)
Ethene (Ethylene) ✘
- Ethene is symmetrical about double bond, therefore will form 100% same molecule (highest yield)
- OH group adds to either of the 1˚ carbons across double bond
- Forms ethanol
2-pentene ✓
- Both carbons are 2˚, therefore there will be equal amounts of the two different products in a 50-50% mix of: 3-pentanol and 2-pentanol
- (The minor product on one is the major product of the other so it is only 50-50)
In the major product, the hydrogen (H) atom attaches to the carbon with fewer alkyl (C) substituents, or the larger number of hydrogen atoms. The hydroxide (OH) group becomes attached to the carbon with more alkyl substituents.
2-methyl-2-butene ✘
- Major product will form with -OH group attached to carbon 2, forming 2-methyl-2-butanol
- OH will add to the 3˚ carbon more than the 2˚ carbon
- (Minor product formed is 3-methyl-2-butanol)
- Ethene is symmetrical about double bond, therefore will form 100% same molecule (highest yield)
- OH group adds to either of the 1˚ carbons across double bond
- Forms ethanol
- Both carbons are 2˚, therefore there will be equal amounts of the two different products in a 50-50% mix of: 3-pentanol and 2-pentanol
- (The minor product on one is the major product of the other so it is only 50-50)
Similar to alkenes, addition of acid halides to alkynes follows Markovnikov's rule.
Solution
The halogen bonds to the more highly substituted carbon... And in the presence of excess acid halide, a further addition reaction will occur to the alkene to produce a di-halide carbon.
Structural (Constitutional) Isomers
Draw three structural (constitutional) isomers of hexane C6H14.
Solution
Video
Draw any three of: hexane, 2-methylpentane, 3-methylpentane, 2,3-dimethylpentane, 2,2-dimethylpentane


Isomers
Isomers must always have the same chemical formula.
Solution
All isomers have the same chemical formula, but either the bonding or the spatial arrangement is/are different.
Two isomers have the same bonding, but different arrangements in across carbon-carbon double bonds. Determine the classification of isomer.
Solution
Constitutional/Structural Isomers
Different bonding
Stereoisomers Isomers
Same bonding, dfferent arrangement... Eg)
- Geometric Diastereomers (different arrangement across C=C bonds)
- Enantiomers (mirror image, non-superimposable)

CC: Yassine Mrabet, 2008
Different bonding
Stereoisomers Isomers
Same bonding, dfferent arrangement... Eg)
- Geometric Diastereomers (different arrangement across C=C bonds)
- Enantiomers (mirror image, non-superimposable)
 |
Types of Isomers (Chart in Answer)
Classify the types of isomers below.
Alkenes...
Solution Video

cis-2-Butene and trans-2-Butene are geometric (cis-trans) isomers, which are under the category of diastereomer and stereoisomer.

CC: Yassine Mrabet, 2008
 |
Branched alkanes...
Solution
Video

Conformational isomers are a type of stereoisomer in which the bonding groups differ by rotation around a single C-C bond.

CC: Yassine Mrabet, 2008
 |
Cyclic molecules...
Solution
Video

These cyclic ether molecules are structural isomers (aka constitutional isomers) because they would have the same chemical formula (C3H6O3), but they have a different bond structure.

CC: Yassine Mrabet, 2008
 |
Cyclic, with side groups...
Solution

These diols (molecules containing two hydroxyl groups) are conformational isomers because the hydoxy group is rotated or flipped-up around a chiral carbon.
These are not enantiomers because they are not non-superimposable mirror images.

CC: Yassine Mrabet, 2008
(Not a diastereomer because does not have double bonds)
(Not constitutional/structural because carbons still have same things bonded to them)
These are not enantiomers because they are not non-superimposable mirror images.
 |
(Not constitutional/structural because carbons still have same things bonded to them)
Chirality: Enantiomers
What are the main requirements for molecules to be considered enantiomers? [2]
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Enantiomers are molecules that have chiral centers, and are non-superimposable mirror images.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
2-bromo-2-methylbutane exhibits chirality.
Solution
Video
Stereoisomers
Two stereoisomers are shown below. Determine the carbon number of the chiral center.
Solution
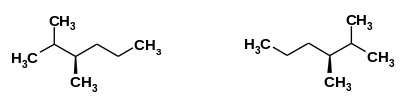 carbon #
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Carbon number 3 has four different groups on each bond, therefore it is a chiral center.
carbon #
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Carbon number 3 has four different groups on each bond, therefore it is a chiral center.
carbon #
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Chiral Centers (Stereocenters)
How many stereoisomers are possible with 3 chiral centers in a molecule?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The number of chiral centers in this Cholesterol molecule is
Solution
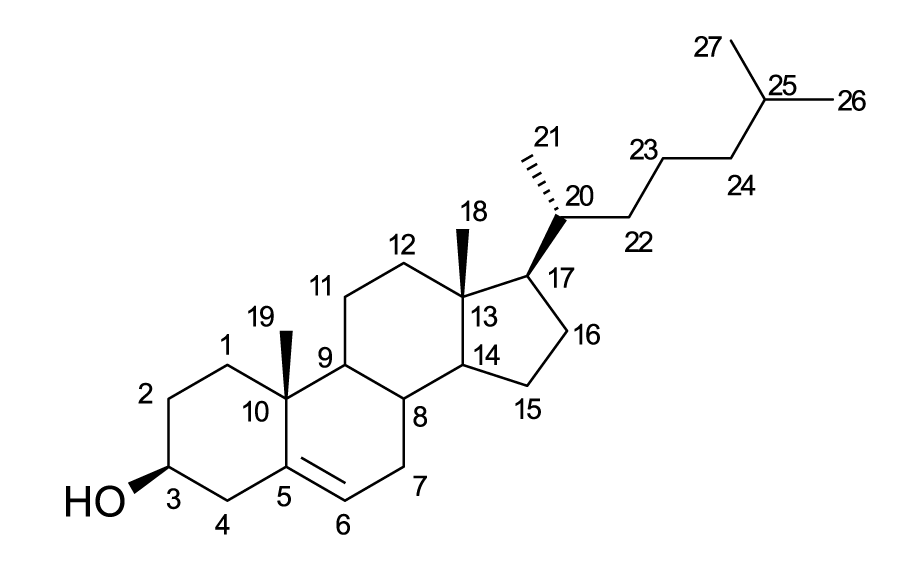 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Chiral centers have different groups on all 4 bonds around a carbon. (Remember that chiral carbons are asymmetric such that the mirror image is non-superimposable.)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Chiral centers have different groups on all 4 bonds around a carbon. (Remember that chiral carbons are asymmetric such that the mirror image is non-superimposable.)
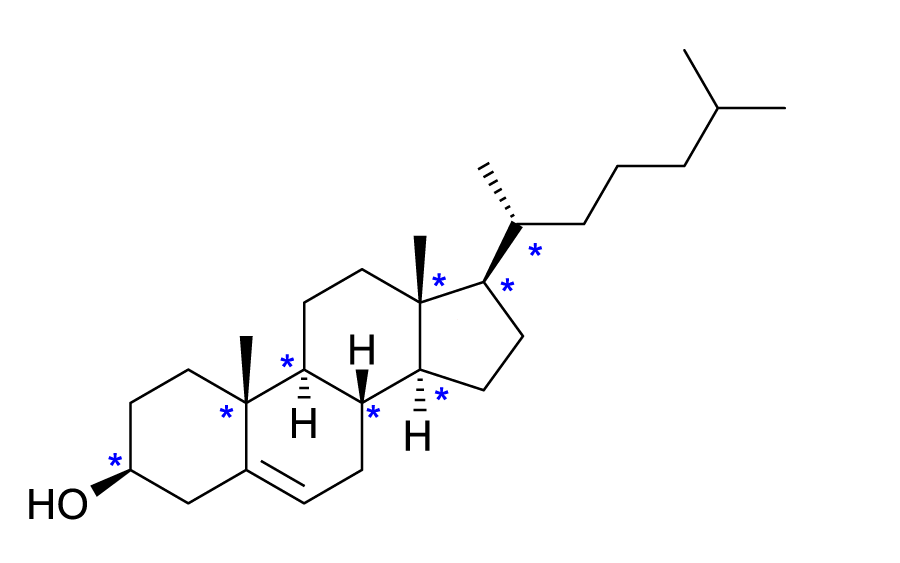
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable

Naming Alcohols
Name the following alcohols using IUPAC naming.
Which of the following synonyms is the correct IUPAC name?
Solution
IUPAC naming places the number next to the parent/functional group suffix...
butan-2-ol
Remember to always drop the last "e" from the hydrocarbon name.
With one alcohol...
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
2-methyl-pentan-2-ol
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
2-methyl-pentan-2-ol

Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable

With two alcohols...
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
2-methyl-pentan-2,3-diol
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
2-methyl-pentan-2,3-diol

Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable

With three alcohols...
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
2-methyl-hexan-2,4,5-triol
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
2-methyl-hexan-2,4,5-triol

Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable

Cyclic with two hydroxide groups
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
cyclopropan-1,2-diol
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
cyclopropan-1,2-diol
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Cyclic with three hydroxide groups, and more...
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Priority:
alcohol > alkene > alkyl
Steps:
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Priority:
alcohol > alkene > alkyl
Steps:
- Find the longest continuous carbon chain
- Start numbering from the side with the highest priority functional group
- Number the side groups with the lowest combination of numbers
- Add carbon numbers, prefixes, and drop the 'e' from root name.
- Order alphabetically
 4-methyl-cyclohex-1-en-1,3,5-triol
4-methyl-cyclohex-1-en-1,3,5-triol
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
- Find the longest continuous carbon chain
- Start numbering from the side with the highest priority functional group
- Number the side groups with the lowest combination of numbers
- Add carbon numbers, prefixes, and drop the 'e' from root name.
- Order alphabetically
 4-methyl-cyclohex-1-en-1,3,5-triol
4-methyl-cyclohex-1-en-1,3,5-triol
Naming Alcohols
The following name is incorrect. Determine the correct name.
Solution
1-methyl-cyclohexane-3-ol
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The alcohol takes priority so you should start numbering from the side with the alcohol... Also you should drop the 'e' at the end of the root name.
3-methyl-cyclohexan-1-ol
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Name the following saturated, branched alcohol molecule.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Steps...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Steps...
- Find the longest continuous carbon chain
- Start numbering from the side with the highest priority functional group
- Number the side groups with the lowest combination of numbers
- Add carbon numbers, prefixes, and drop the 'e' from root name.
- Order alphabetically
 4,7-diethyl-3,7-dimethyl-decan-2-ol
4,7-diethyl-3,7-dimethyl-decan-2-ol
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
- Find the longest continuous carbon chain
- Start numbering from the side with the highest priority functional group
- Number the side groups with the lowest combination of numbers
- Add carbon numbers, prefixes, and drop the 'e' from root name.
- Order alphabetically
 4,7-diethyl-3,7-dimethyl-decan-2-ol
4,7-diethyl-3,7-dimethyl-decan-2-ol
Name the following unsaturated alcohol molecule.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The alcohol has the highest priority, so start numbering from that end... 3,7-dimethyl-oct-6-en-1-ol
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The alcohol has the highest priority, so start numbering from that end... 3,7-dimethyl-oct-6-en-1-ol
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Terminology of Alcohols
Determine whether the following molecules are primary, secondary, or tertiary...
This ethanol (alcohol) molecule.
Solution

Primary, 1˚ because the carbon attached to the hydroxide group is attached to 1 other carbon.
This branched alcohol.
Solution

Tertiary, 3˚ because the carbon attached to the hydroxide group is attached to three other carbons.
This cyclic (cyclohexan-1-ol) alcohol.
Solution

Secondary, 2˚ because the carbon attached to the hydroxide group is attached to two other carbons.
Physical Properties: Melting & Boiling Points of Alcohols
Alcohols are composed of a non-polar, hydrophobic alkyl group (CXHY), and a polar, hydrophilic hydroxide group (OH). The electrostatic dipole in the hydroxide group allows the non-polar chain to dissolve in water.
CXHY—OHMelting and boiling point of alcohols depends on what two main factors? [2]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Molecular weight and side group branching.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Which of the following alcohols has the highest boiling point?
Solution

Because it can form the most hydrogen bonds, which makes the intermolecular force strong and increases the boiling point (the point at which intermolecular forces are overcome in the liquid phase to spread apart into the gas phase).
Reaction: Hydration of Alkene Produces Alcohol
Hydration of propene mainly produces
Solution
Video
Markovnikov's Rule
The hydrogen (H) attaches to the carbon atom with the most hydrogens, while the hydroxide (OH) attaches to the carbon with the highest alkyl substitution
The hydrogen (H) attaches to the carbon atom with the most hydrogens, while the hydroxide (OH) attaches to the carbon with the highest alkyl substitution
Reactions: Addition (Hydration) Reactions
Complete the reaction (draw in your notes) and name the product formed.
Solution
Video
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Markovnikov's Rule
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Markovnikov's Rule
The hydrogen (H) attaches to the carbon atom with the most hydrogens, while the hydroxide (OH) attaches to the carbon with the highest alkyl substitution.

3-methyl-hexan-3-ol
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The hydrogen (H) attaches to the carbon atom with the most hydrogens, while the hydroxide (OH) attaches to the carbon with the highest alkyl substitution.

3-methyl-hexan-3-ol
Reaction: Elimination (Dehydration) of Alcohol
Treating an alcohol with concentrated sulfuric acid (H2SO4) produces the following molecule. What would the starting molecule have been?
Solution
Video
 The concentrated sulfuric acid (H2SO4) catalyzes the dehydration of the alcohol in the starting molecule.
The concentrated sulfuric acid (H2SO4) catalyzes the dehydration of the alcohol in the starting molecule.
A hydrogen (H) and a neighboring hydroxyl (OH) group is then removed, resulting in the formation of a double bond (C=C).
Answer choice 'C' is incorrect because the dehydration of this alcohol would yield a major product with an internal double bond on more highly substituted carbons.
A hydrogen (H) and a neighboring hydroxyl (OH) group is then removed, resulting in the formation of a double bond (C=C).
Answer choice 'C' is incorrect because the dehydration of this alcohol would yield a major product with an internal double bond on more highly substituted carbons.
Reactions: Combustion of Alcohols
Complete combustion of one mole of 3-ethyl-2-methylhexan-1-ol would yield how many moles of carbon dioxide?
Solution
Video
 Hint
Clear
Info
Incorrect Attempts:
CHECK
mol
Hint Unavailable
The moles of carbon dioxide equals the number of carbons in one mole of the alcohol molecule.
Hint
Clear
Info
Incorrect Attempts:
CHECK
mol
Hint Unavailable
The moles of carbon dioxide equals the number of carbons in one mole of the alcohol molecule.
CxHYOZ + mO2 --> xCO2 + nH2O
Hint
Clear
Info
Incorrect Attempts:
CHECK
mol
Hint Unavailable
CxHYOZ + mO2 --> xCO2 + nH2O
Naming Aldehydes
The name of the following molecule is
Solution
Video
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Recognize the aldehyde functional group; aldehydes take the suffix -al
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Recognize the aldehyde functional group; aldehydes take the suffix -al
The backbone is 5 carbons long, so it takes the root name pentan-... = pentanal.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The backbone is 5 carbons long, so it takes the root name pentan-... = pentanal.
Naming Aldehydes
Name the following molecules
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
4-methylpentanal
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
4-methylpentanal
Start numbering from the higher priority functional group - the aldehyde.

Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Start numbering from the higher priority functional group - the aldehyde.

Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
5-bromo-7-hydroxy-4-methylheptanal
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
5-bromo-7-hydroxy-4-methylheptanal
Start numbering from the higher priority functional group - the aldehyde.

Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Start numbering from the higher priority functional group - the aldehyde.

Physical Properties of Aldehydes
Propanal has a lower boiling point than butane.
Solution

Propanal has a higher boiling point than butane. Due to: higher polarity and dipole-dipole interaction in the aldehyde.
Which of the following compounds has the lowest boiling point?
Solution
Between equivalent aldehydes and alcohols, like hexanal and hexanal, the aldehyde will always have the lower boiling point. Aldehydes cannot hydrogen bond!
Of course, molecules with lower molecular weights have lower boiling points (between hexanal and octanal).
Of course, molecules with lower molecular weights have lower boiling points (between hexanal and octanal).
Structural Isomers: Aldehyde
Which of the following is a structural isomer of 1-propanal?
Solution
Structural isomers (aka constitutional isomers) have the same chemical formula, but have different bond connectivity in their structures.
1-propanal is an aldehyde, and aldehydes have structural isomers with ketones (with same chemical formula).
1-propanal is an aldehyde, and aldehydes have structural isomers with ketones (with same chemical formula).
Reactions: Oxidation of Alcohols
In the presence of a strong oxidizing agent, propan-1-ol is fully oxidized into propanal as the end product.
Solution
A strong oxidizing agent will not stop at propanal, and will continue oxidation to form propanoic acid.
(To make aldehydes, a primary alcohol must be oxidized with a weak oxidizer like PCC).
(To make aldehydes, a primary alcohol must be oxidized with a weak oxidizer like PCC).
Reactions of Aldehydes
Determine the name of the product of the following reaction.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hydrogenation of an aldehyde will reduce it to an alcohol
Hydrogenation of an aldehyde will reduce it to an alcohol... propanol
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hydrogenation of an aldehyde will reduce it to an alcohol
Hydrogenation of an aldehyde will reduce it to an alcohol... propanol
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hydrogenation of an aldehyde will reduce it to an alcohol
Naming Ketones
Name the following ketone molecules.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Accept butanone (or 2-butanone), when the molecule is superimposable when rotated in 3D space, you don't have to indicate the carbon number. There is no other possible position for the internal carbonyl carbon in a butane chain.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Accept butanone (or 2-butanone), when the molecule is superimposable when rotated in 3D space, you don't have to indicate the carbon number. There is no other possible position for the internal carbonyl carbon in a butane chain.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
4-methyl-2-pentanone
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
4-methyl-2-pentanone
Start numbering from the end with the higher priority functional group - the ketone.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Start numbering from the end with the higher priority functional group - the ketone.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
3-methyl-2,6-heptdione
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
3-methyl-2,6-heptdione
Start numbering from the end with the higher priority functional group - the ketone.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Start numbering from the end with the higher priority functional group - the ketone.
Structural (Constitutional) Isomers of Ketones
Ketones have structural (constitutional) isomers that are aldehydes.
Solution
As long as it has the same molecular formula.
Draw a structural (constitutional) isomer of 3-methylpentanal.
Solution
Draw any ketone or aldehyde, with the same molecular formula. (not shown)
4-methyl-2-pentanone and 3-methylpentanal are structural isomers.
Solution
These two ketone and aldehyde molecules have the same molecular formula: C6H12O.
Properties of Ketones
Ketones have boiling points slightly higher than aldehydes of the same carbon chain length.
Solution
The molecular weight of ketones is slightly higher than that of aldehydes.
Reactions of Ketones: Oxidation of Alcohols
Oxidation of the following molecule will yield which product (if any)?
Solution

Tertiary (3˚ alcohols) do not react in oxidation reactions since further oxidation from the alcohol would make a double bond, and there is no space for additional bonds on the central carbon atom.
A tertiary alcohol is oxidized to form a ketone in the presence of potassium permanganate (KMnO4).
Solution
Although potassium permanganate (KMnO4) is a very strong oxidizer, 3˚ alcohols cannot be oxidized to produce a ketone group. Only 1˚ and 2˚ alcohols can do this, although oxidation of 1˚ alcohols form aldehydes or carboxylic acids rather than ketones.
Terminology of Carboxylic Acids
The standard name of the -COOH group in the diagram below is:
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The -COOH group is a carboxyl. (The -C=O group is a carbonyl).
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The -COOH group is a carboxyl. (The -C=O group is a carbonyl).
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Naming Carboxylic Acids
Name the following carboxylic acid molecules.
With a halide...
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
4-bromopentanoic acid
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
4-bromopentanoic acid
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
With lots of branching...
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
2-ethyl-3,5-dimethylheptanoic acid
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
2-ethyl-3,5-dimethylheptanoic acid

Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable

With two carboxyl groups...
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
butandioic acid
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
butandioic acid
(Notes: drop the 'e' and don't have to indicate 1,4 because carboxylic acids have to be terminal.)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(Notes: drop the 'e' and don't have to indicate 1,4 because carboxylic acids have to be terminal.)
Properties of Carboxylic Acids
Order the following molecules in order of decreasing boiling point from top to bottom.
Solution
Pentanal
Pentane
Pentanol
Pentanoic acid
If the molecular weights are all the same then...
The boiling point is based on the strength of the primary intermolecular force: hydrogen bonds are strongest, then dipole-dipole, then London dispersion.
Carboxylic acids have hydroxide groups (-OH) that have the strongest hydrogen bonding.
Alcohols have hydroxide groups (-OH) that hydrogen bond, but are less strong than the ones in carboxylic acids.
Amines have amino groups (-NH) that hydrogen bond, but are even weaker than alcohols.
Alkanes have very weak London dispersion intermolecular forces.
The boiling and melting points from high to low:
carboxylic acid → alcohol → aldehyde → alkane
Pentanal
Pentane
Pentanol
Pentanoic acid
The boiling point is based on the strength of the primary intermolecular force: hydrogen bonds are strongest, then dipole-dipole, then London dispersion.
Carboxylic acids have hydroxide groups (-OH) that have the strongest hydrogen bonding.
Alcohols have hydroxide groups (-OH) that hydrogen bond, but are less strong than the ones in carboxylic acids.
Amines have amino groups (-NH) that hydrogen bond, but are even weaker than alcohols.
Alkanes have very weak London dispersion intermolecular forces.
The boiling and melting points from high to low:
carboxylic acid → alcohol → aldehyde → alkane
Reactions of Carboxylic Acids
Oxidation of which molecule will produce the following carboxylic acid?
Solution

Oxidation of alcohols with a strong oxidizing agent like potassium permanganate (KMnO4) will make carboxylic acids.
Naming Esters
Name the following ester molecules.
With an alkane chain on the oxygen...
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
butyl methanoate
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
butyl methanoate

Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable

With an alkane chain on the carbonyl carbon...
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
methyl pentanoate
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
methyl pentanoate

Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable

With chains all over...
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
3-pentyl 2-ethylbutanoate
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
3-pentyl 2-ethylbutanoate
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Naming Esters
Name the following ester molecule.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
3-chlorobutan-1-ol 4-bromo-3-methylbutanoate
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
3-chlorobutan-1-ol 4-bromo-3-methylbutanoate

Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable

Properties of Esters
Different ester molecules have a wide range of characteristic odours. Smells are detected by olfactory receptors in the nose when an ester molecule lands on one of the receptors. Which molecule would have the strongest smell at room temperature?
Solution
To detect the smell, the ester molecule must be evaporated into the air as a gas. The molecule that evaporates most will have a relatively low boiling point; with a lower molecular weight. The long chain molecules will not vaporize at room temperature and not be easily detected.
Ester Reactions: Esterification
In the presence of heat and an acid, ethanol + acetic acid will produce an ester with four carbons.
Solution
Ethanol + Acetic Acid --> Ethylacetate
Ester Reactions: Synthesis of Esters
Esters are formed in a condensation reaction when hydrogen (-H) from a carboxylic acid and a hydroxyl (-OH) group from alcohol combine to form a water molecule, in the presence of heat.
Solution
Esters are formed when the hydroxyl (-OH) from a carboxylic acid and a hydrogen (-H) from alcohol combine to form a water molecule, in the presence of heat.
State the reactants required to synthesize the following molecule and provide the name for this Ester.
Solution

Alcohol + Carboxylic acid → Ester
(This is a dehydration reaction)
(This is a dehydration reaction)
Ester Reactions: Hydrolysis
Sodium hydroxide is added to a propylmethanoate ester, shown below. Determine (in your notes) the molecular structure of the conjugate base and conjugated acid products.
Solution



The following process is called...
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The ester bonds in triglycerides (fats, lipids) are cleaved with the base (NaOH), which creates an alcohol (glycerol) and a carboxylate anion salt with the sodium. This is basically how soap is made... saponification
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Naming Ethers
Name the following ether.
Solution
CH3CH2CH2CH2CH2-O-CH2CH2CH2CH3
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Take the longest carbon chain (-pentane) and that is the backbone. Then add the other chain on the oxygen (but-) as the prefix...
butoxypentane
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
butoxypentane
Properties of Ethers
The boiling point of butane is higher than the boiling point of ethoxyethane (diethyl ether).
Solution
The boiling point of butane is lower than the boiling point of ethoxyethane (diethyl ether). This is due to the polarity of the C-O bonds in ethers being higher than the polarity of C-C bonds in the alkane, resulting in greater intermolecular forces and an increase in boiling point.
Reactions: Ether Dehydration Reaction
Fill in the missing reactant, X, for the following condensation reaction.
Solution
This is a condensation reaction between a hydroxyl, OH group from one alcohol and a hydrogen, H from another alcohol.
Terminology of Amines
Match the molecule with the correct classification.
Solution

 Primary (1˚)
Secondary (2˚)
Tertiary (3˚)
Quaternary (4˚)
Both amine molecules are primary (1˚) because the nitrogen is attached to 1 carbon.
Primary (1˚)
Secondary (2˚)
Tertiary (3˚)
Quaternary (4˚)
Both amine molecules are primary (1˚) because the nitrogen is attached to 1 carbon.


Primary (1˚)
Secondary (2˚)
Tertiary (3˚)
Quaternary (4˚)
The following molecule is classified as:
Solution

Secondary (2˚) amines are bonded to 2 carbons. (1˚ amines are bonded to 1 carbon, and 3˚ amines are bonded to 3 carbons).
Naming Amines
Name the following molecule with IUPAC nomenclature.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
N-ethyl-N-methylaminopropane
The highest carbon chain gets the root name, while the remaining substituents are numbered with N and listed in alphabetical order. (Sometimes can be named with non-Iupac: ethylmethylpropylamine, or when CA naming convention: N-ethyl-N-methylpropanamine)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
N-ethyl-N-methylaminopropane
The highest carbon chain gets the root name, while the remaining substituents are numbered with N and listed in alphabetical order. (Sometimes can be named with non-Iupac: ethylmethylpropylamine, or when CA naming convention: N-ethyl-N-methylpropanamine)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Naming Amines
Name the following amine molecules.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
N-ethyl-2-aminobutane
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
N-ethyl-2-aminobutane
(or with CA naming convention: N-ethyl-2-butanamine)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(or with CA naming convention: N-ethyl-2-butanamine)
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
1,3-diaminopropane
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
1,3-diaminopropane
(or with CA naming convention: 1,3-propanediamine)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(or with CA naming convention: 1,3-propanediamine)
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
N-ethyl-N-methylaminoethane
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
N-ethyl-N-methylaminoethane
(or with CA naming convention: N-ethyl-N-methyl-1-ethanamine)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(or with CA naming convention: N-ethyl-N-methyl-1-ethanamine)
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
2-amino-3-methylhexane
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
2-amino-3-methylhexane
(or with CA naming convention: 3-methyl-2-hexanamine)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(or with CA naming convention: 3-methyl-2-hexanamine)
Solution
Video
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The ethyl group on the amine (N-ethyl) gets named first. The longest carbon-chain backbone is 10 carbons, decane...
N-ethyl-5-amino-2,9-dimethyl-5-propyldecane
(or CA naming convention: N-ethyl-2,9-dimethyl-5-propyl-5-decylamine)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The ethyl group on the amine (N-ethyl) gets named first. The longest carbon-chain backbone is 10 carbons, decane...
N-ethyl-5-amino-2,9-dimethyl-5-propyldecane
(or CA naming convention: N-ethyl-2,9-dimethyl-5-propyl-5-decylamine)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Naming Amines
Two lab partners are trying to name an amine product but they are in a disagreement over the correct IUPAC name. Determine who is correct.
Sydney wants to name it 2-chloro-4-aminoheptane, but Caroline wants to name it 4-amino-2-chloroheptane.
Solution
Caroline has the correct name:
4-amino-2-chloroheptane
(Also acceptable would be the CA naming convention for amines: 2-chloro-4-heptanamine)
Jukka wants to name it 3-amino-2-bromo-N-methyl-1-hexene, but Koji wants to name it N-methyl-3-amino-2-bromo-1-hexene.
Solution
Koji has the correct name:
N-methyl-3-amino-2-bromo-1-hexene
(In this example we would not use the -amine naming convention according to CA rules because the double bond has priority in the naming system).
Properties of Amines
All pure primary, secondary, and tertiary amines can hydrogen-bond.
Solution
Only primary and secondary amines have N-H bonds that can hydrogen bond. The N-C bonds in tertiary amines cannot hydrogen bond.
Properties of Amines
Order the following molecules in order of increasing boiling point (from bottom to top) by dragging them.
Solution
Video
Hexanol
Hexanamine
Hexane
Hexanoic acid
Hexanoic acid has the strongest hydrogen bonding and highest molecular weight, so it has the highest boiling point. Hexanol can hydrogen bond. Hexanamine can hydrogen bond but has a lower boiling point than hexanol because the N-H dipole is weaker than the O-H dipole in the alcohol.
Hexanol
Hexanamine
Hexane
Hexanoic acid
Reactions of Amines with Alkyl Halides
Draw and name the products (if any) of the following reactions between an amine and alkyl halide.
Solution
 There is no reaction. A tertiary (3˚) amine will not react because there is no hydrogen on the Nitrogen atom.
There is no reaction. A tertiary (3˚) amine will not react because there is no hydrogen on the Nitrogen atom.
Solution
 = N-ethyl-N-propyl-2-aminopentane + Hydrogen bromide
= N-ethyl-N-propyl-2-aminopentane + Hydrogen bromide


Solution
 = N-Ethylpropanamine + Hydrogen chloride
= N-Ethylpropanamine + Hydrogen chloride
 (or N-ethylaminopropane, or N-Ethylpropylamine)
(or N-ethylaminopropane, or N-Ethylpropylamine)
 (or N-ethylaminopropane, or N-Ethylpropylamine)
(or N-ethylaminopropane, or N-Ethylpropylamine)
Functional Groups
Name the following functional group.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
You should recognize the functional group, amide.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
You should recognize the functional group, amide.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Naming Amides
Name the following amide molecules.
Solution
Video
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
N-ethyl butanamide
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
N-ethyl butanamide
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
N,N-diethyl ethanamide
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
N,N-diethyl ethanamide
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Video
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
N,N-diethyl-3-methylpentanamide
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
N,N-diethyl-3-methylpentanamide
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Physical Properties of Amides
N-propyl-3-methyl butanamide can hydrogen bond.
Solution
The N-H bond in the amide is capable of hydrogen bonding.
Amide Condensation Reactions
Which of the following molecules cannot react with ethanoic acid in a condensation reaction?
Solution
Tertiary (3˚) amines like N,N-dimethylaminopropane cannot react in a condensation reaction with ethanoic acid because this reaction requires at least one N-H bond. All the other amines listed can react.
Synthesizing Amides
N,N-dimethyl butanamide can be synthesized from
Solution
Video
Draw the N,N-dimethyl butanamide amide molecule first to visualize the bonding.
To form the amide bond (C-N), there must have been a condensation (dehydration) reaction between a secondary (2˚) amine and carboxylic acid.

To form the amide bond (C-N), there must have been a condensation (dehydration) reaction between a secondary (2˚) amine and carboxylic acid.

Reactions of Amides
Complete the following reactions and name the products.
[Hydrolysis]
Solution
Video
 N-ethyl propanamide + water → propanoic acid + 1-amino ethane (ethylamine)
N-ethyl propanamide + water → propanoic acid + 1-amino ethane (ethylamine)


[Condensation]
Solution
Video
 3-methyl-butanoic acid + N-methyl-1-amino ethane → N-ethyl-N,3-dimethyl propanamide + water
3-methyl-butanoic acid + N-methyl-1-amino ethane → N-ethyl-N,3-dimethyl propanamide + water


Amides
Protein molecules can be split by adding water, separating into amino acids.
Solution
Protein molecules are polypeptide chains (polymers) joined together with amide bonds. These amide bonds can be hydrolyzed, broken with water.
Carbonyl Groups
Carbonyl (-C=O) groups are present in all of the following molecules:
Solution
Ester, Ketone, Amide, Carboxylic Acid, Aldehyde
Carbonyl groups are carbon atoms that are double-bonded to oxygen.
Naming Simple Aromatic Hydrocarbons
The common name for this aromatic molecule is:
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
...phenol (this is a benzene ring with one alcohol side group)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
...phenol (this is a benzene ring with one alcohol side group)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Benzene Structures
What is ortho, meta, and para and when are they used? [1]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The ortho, meta, and para naming system is an alternative system that is used when benzene rings are substituted with exactly 2 side groups. This naming system cannot be used when benzene has 1 or 3+ side groups.
Ortho side groups are on adjacent carbons. Meta side groups are on carbons that have one carbon between them. Para side groups are on carbons with two other carbons between them.

Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Ortho side groups are on adjacent carbons. Meta side groups are on carbons that have one carbon between them. Para side groups are on carbons with two other carbons between them.

Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
1-ethyl-3-methylbenzene
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
1-ethyl-3-methylbenzene
(aka m-methyl ethyl benzene) -- the ortho/meta/para nomenclature is interchangeable with the other naming system, but can only be used with two side groups. The other system can be used with two or more side groups.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(aka m-methyl ethyl benzene) -- the ortho/meta/para nomenclature is interchangeable with the other naming system, but can only be used with two side groups. The other system can be used with two or more side groups.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
4-methyl-1-propylbenzene
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
4-methyl-1-propylbenzene
The higher molecular weight propyl takes priority over methyl.
The substituents should be in alphabetical order with 'm' before 'p'. So 1-propyl-4-methylbenzene is not entirely correct.
(aka p-methyl propyl benzene) -- the ortho/meta/para nomenclature is interchangeable with the other naming system, but can only be used with two side groups. The other system can be used with two or more side groups.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The higher molecular weight propyl takes priority over methyl.
The substituents should be in alphabetical order with 'm' before 'p'. So 1-propyl-4-methylbenzene is not entirely correct.
(aka p-methyl propyl benzene) -- the ortho/meta/para nomenclature is interchangeable with the other naming system, but can only be used with two side groups. The other system can be used with two or more side groups.
Aromatic Hydrocarbons: Alyklbenzene
Name the following, which have benzene as a substituent.
Solution
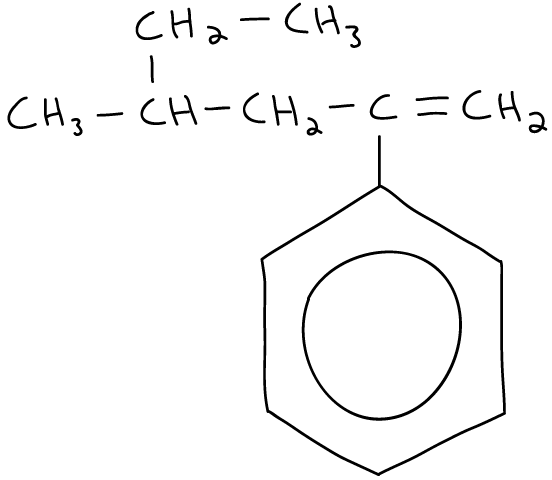 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
4-methyl-2-phenyl-1-hexene.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
4-methyl-2-phenyl-1-hexene.
(Benzene becomes phenyl as a side group).
The substituents should be in alphabetical order with 'm' before 'p'.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(Benzene becomes phenyl as a side group).
The substituents should be in alphabetical order with 'm' before 'p'.
Solution
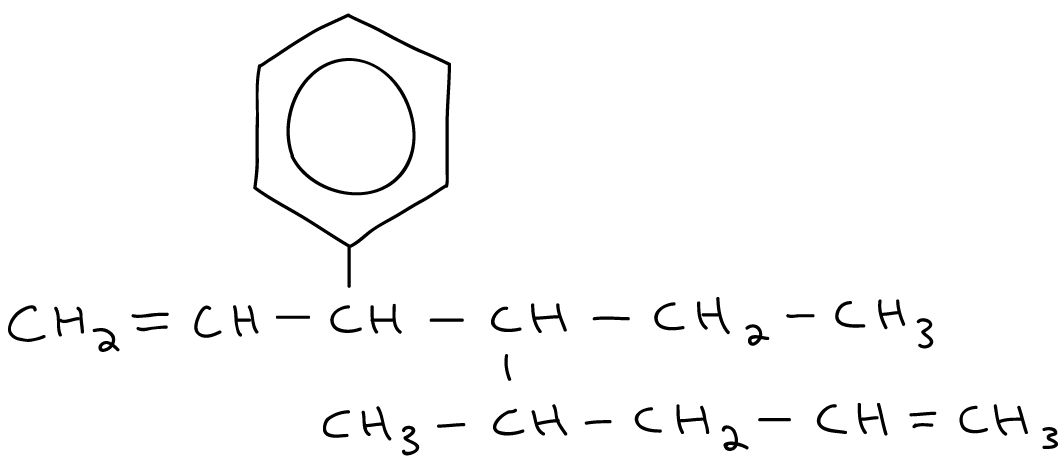 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
4-ethyl-5-methyl-3-phenyl-1,8-octadiene
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
4-ethyl-5-methyl-3-phenyl-1,8-octadiene
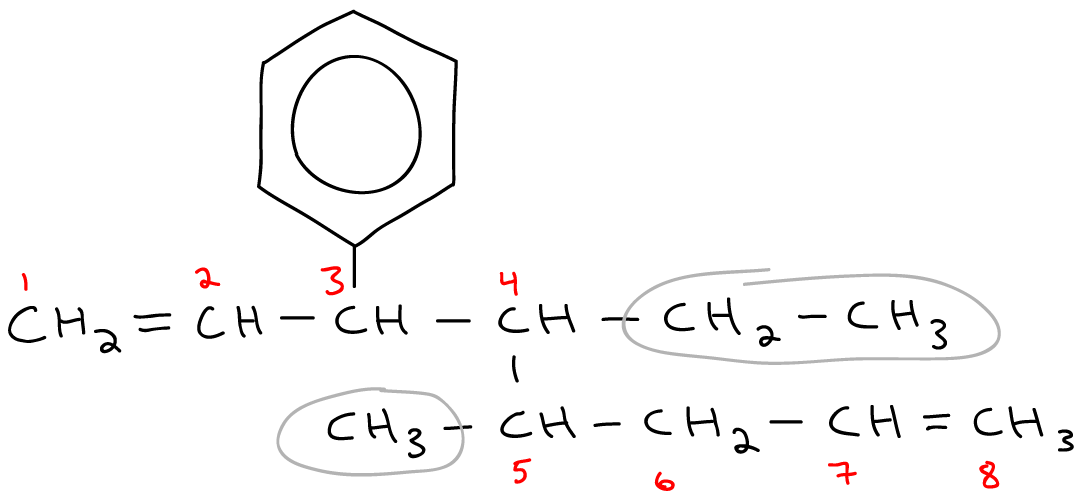
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable

Reactions of Aromatics
Given a simple benzene molecule as the reactant, what happens when it is reacted with...

Excess Cl2 (g) in the presence of AlCl3 at room temperature?
Solution
 At room temperature (and at regular pressure) the benzene ring maintains aromaticity (the double bond arrangement) and is substituted by one halogen.
At room temperature (and at regular pressure) the benzene ring maintains aromaticity (the double bond arrangement) and is substituted by one halogen.
 At room temperature (and at regular pressure) the benzene ring maintains aromaticity (the double bond arrangement) and is substituted by one halogen.
At room temperature (and at regular pressure) the benzene ring maintains aromaticity (the double bond arrangement) and is substituted by one halogen.
Excess Cl2 (g) in the presence of AlCl3 with heat (∆) at 300˚C and UV light (hv)?
Solution
 See the benzene ring loses aromaticity to become a substituted cyclohexane.
See the benzene ring loses aromaticity to become a substituted cyclohexane.
 See the benzene ring loses aromaticity to become a substituted cyclohexane.
See the benzene ring loses aromaticity to become a substituted cyclohexane.
Excess H2 (g) in the presence of heat (∆) and Platinum (Pt) or Nickel (Ni) catalysts.
Solution
 Hydrogenation removes the aromaticity of the benzene ring to form cyclohexane.
Hydrogenation removes the aromaticity of the benzene ring to form cyclohexane.
 Hydrogenation removes the aromaticity of the benzene ring to form cyclohexane.
Hydrogenation removes the aromaticity of the benzene ring to form cyclohexane.
The alkyl halide, chloroethane in the presence of AlCl3.
Solution
 Friedel-Crafts actylation adds the alkyl group attached to the chlorine to the benzene ring. The byproduct is hydrochloric acid where the hydrogen is from the benzene ring and the chlorine is from the alkyl halide substrate.
Friedel-Crafts actylation adds the alkyl group attached to the chlorine to the benzene ring. The byproduct is hydrochloric acid where the hydrogen is from the benzene ring and the chlorine is from the alkyl halide substrate.
 Friedel-Crafts actylation adds the alkyl group attached to the chlorine to the benzene ring. The byproduct is hydrochloric acid where the hydrogen is from the benzene ring and the chlorine is from the alkyl halide substrate.
Friedel-Crafts actylation adds the alkyl group attached to the chlorine to the benzene ring. The byproduct is hydrochloric acid where the hydrogen is from the benzene ring and the chlorine is from the alkyl halide substrate.
Reactions of Aromatics
Determine the product when phenylmethanol is oxidized in a controlled oxidation.
Solution
 The controlled oxidation of phenylmethanol will produce benzaldehyde...
The controlled oxidation of phenylmethanol will produce benzaldehyde...


Polymers
Polymers are made of identical monomer subunits.
Solution
It is true that polymers are made of many monomer subunits, but the monomer subunits do not have to be identical when joined by addition or condensation polymerization.
Which one of the following common molecules is not a polymer?
Solution
Glucose is not a polymer because it is a monomer! Glucose is a monosaccharide like the monomers that make polysaccharide polymers like starch or cellulose...
Examples of polymers...
- Polysaccharides (starch, cellulose...)
- Deoxyribonucleic Acid (DNA)
- Synthetic polymers (like Nylon, Teflon, Polyeser...)
- Proteins
- Rubber (vulcanized)
Examples of polymers...
- Polysaccharides (starch, cellulose...)
- Deoxyribonucleic Acid (DNA)
- Synthetic polymers (like Nylon, Teflon, Polyeser...)
- Proteins
- Rubber (vulcanized)
Carbohydrates and Amino Acids
Carbohydrates and amino acids are polymers.
Solution
Amino acids are monomers, the polymer of amino acids is a protein (polypeptide).
Amino Acid Polymerization
Fill in the blank: Polymerization of amino acids through a _____________ reaction creates a bond between ______________ atoms.
Solution

Polysaccharides
Sucrose is a polysaccharide made from the monosaccharide subunits
Solution
Polysaccharides are polymers of simple sugar molecules. In this case, Sucrose is a polysaccharide made from Glucose and Fructose.
Polymerization
The condensation reaction to polymerize the following molecules will form what monomer subunit?
Solution
Video

A carboxylic acid on one molecule and an alcohol on another molecule condense (dehydrate) to form the ester linkage (...CH2OOCCH2...) plus a water molecule H-OH.
 = [—OCH2CH2OOCCH2CH2CO—]n
= [—OCH2CH2OOCCH2CH2CO—]n
 = [—OCH2CH2OOCCH2CH2CO—]n
= [—OCH2CH2OOCCH2CH2CO—]n
Polymerization of Alkenes
Draw the monomer subunit when 3-bromo-5-methyl-1,6-heptadiene undergoes polymerization
Solution



Draw (in your own notes) and name the monomer subunit in the following polymer.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The monomer subunit is...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The monomer subunit is...
 BUT, it's considered best form to name the monomer before it polymerizes...
BUT, it's considered best form to name the monomer before it polymerizes...
 1-bromo-2-chloro-ethene (not 1-bromo-2-chloro-ethane)
1-bromo-2-chloro-ethene (not 1-bromo-2-chloro-ethane)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
 BUT, it's considered best form to name the monomer before it polymerizes...
BUT, it's considered best form to name the monomer before it polymerizes...
 1-bromo-2-chloro-ethene (not 1-bromo-2-chloro-ethane)
1-bromo-2-chloro-ethene (not 1-bromo-2-chloro-ethane)
Polymerization of Carboxylic Acids and Amines
Draw the monomer subunit that forms when a di-carboxylic acid, butanedioic acid undergoes polymerization with a di-amine, N,N-dimethyl-1,3-diaminopropane.
Solution
Video
 This condensation reaction (dehydration of a water molecule) will create an amide bond. The monomer subunit contains one of each 'type' of molecule and shows the repeating unit as if it had undergone the polymerization (condensation in this case) reactions on both ends of the monomer subunit molecule.
This condensation reaction (dehydration of a water molecule) will create an amide bond. The monomer subunit contains one of each 'type' of molecule and shows the repeating unit as if it had undergone the polymerization (condensation in this case) reactions on both ends of the monomer subunit molecule.


Other: Free Radical Mechanism
The steps shown in the following chain mechanism of free radicals is called
Solution

In these steps you can see the free radical propagating through to the next molecules in a chain reaction.
Naming Functional Groups
Name all of the functional groups present in this molecule. [5]
Solution

Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Benzene, Amine, Amide, Alkene, Ether
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Priority of Naming with Multiple Functional Groups
Name the following molecule given the priority table below.
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
| Priority Ranking | Functional Group |
| 1 (Highest Priority) | Carboxylic acid |
| 2 | Ester |
| 3 | Amide |
| 4 | Aldehyde |
| 5 | Ketone |
| 6 | Alcohol |
| 7 | Amine |
| 8 | Ether |
| 9 | Alkene |
| 10 | Alkyne |
| 11 | Halide |
| 12 (Lowest Priority) | Alkane branch |
5-amino-3-hydroxy-oct-7-enoic acid
Carboxylic acids rank highest on the list. Start numbering from the carbonyl carbon on the carboxylic acid functional group.
Carboxylic acids rank highest on the list. Start numbering from the carbonyl carbon on the carboxylic acid functional group.
Synthesis
Determine the structure of each unknown molecule in the pathways below.
The two possible molecules that would make the given alcohol in the reactions below.
Solution



The molecules along the pathway to form the ester.
Solution



Starting with an alkene.
Solution



Starting with an alkene and ending with an amide.
Solution



Flashcards: Organic Chemistry
| What is the prefix of an alkane with 1 carbon? |
| meth |
| What is the prefix of an alkane with 2 carbons? |
| eth |
| What is the prefix of an alkane with 3 carbons? |
| prop |
| What is the prefix of an alkane with 4 carbons? |
| but |
| What is the prefix of an alkane with 5 carbons? |
| pent |
| What is the prefix of an alkane with 6 carbons? |
| hex |
| What is the prefix of an alkane with 7 carbons? |
| hept |
| What is the prefix of an alkane with 8 carbons? |
| oct |
| What is the prefix of an alkane with 9 carbons? |
| non |
| What is the prefix of an alkane with 10 carbons? |
| dec |
Name: |
| 2,4-dimethylpenta-1,5-diene |
Name: |
| 3-chloro-1-ethyl-6-methylcyclohexene |
| Which of the following functional groups is the highest priority, receiving the lower number in the molecule name? Alkyne, Ester, Alcohol |
| The Ester is the highest priority. Order: Carboxylic acid → Ester → Amide → Aldehyde → Ketone → Alcohol → Amine → Ether → Alkene → Alkyne → Alkyl halide |
| What is the functional group in CH3COOH? |
| COOH is a carboxylic acid |
| What are the prefix and suffix for an alcohol? |
| Prefix: hydroxy- Suffix: -ol |
| What are the prefix and suffix for a ketone |
| Prefix: oxo- Suffix: -one |
| What are the prefix and suffix for an aldehyde? |
| Prefix: oxo- Suffix: -al |
| What are the prefix and suffix for a carboxylic acid? |
| Prefix: carboxy- Suffix: -oic acid |
| What is the suffix for an ester? |
| -oate |
| What is the suffix for an ether? |
| -ether |
| What is the suffix for an amide? |
| -amide |
| What are the prefix and suffix for an amine? |
| Prefix: amino- Suffix: -amine |
Name: |
2-methyl-pentan-2-ol |
Name: |
2-methyl-pentane-2,3-diol |
Name: |
4-methylpentanal |
Name: |
5-bromo-7-hydroxy-4-methylheptanal  |
Name: |
| 4-methyl-2-pentanone |
Name: |
| 3-methyl-2,6-heptadione |
Name: |
| 4-bromopentanoic acid |
Name: |
butyl methanoate  |
Name: |
methyl pentanoate  |
| Name: CH3CH2CH2CH2CH2-O-CH2CH2CH2CH3 |
| butoxypentane |
Name: |
| N-ethyl-N-methylpropanamine |
Name: |
| N-ethyl-2-aminobutane |
Name the functional group: |
| Amide |
Name: |
| N-ethyl butanamide |
Name: |
| N,N,3-triethyl butanamide |
Name: |
| 1-ethyl-3-methylbenzene |
Name: |
| 4-methyl-2-phenyl-1-hexene |
| What is a constitutional isomer? |
| A constitutional (or structural) isomer has different connectivity of atoms with the same chemical formula |
| What is the difference between a constitutional isomer and a sterioisomer? |
| While the chemical formula of each isomers remains the same, constitutional isomers have different connectivity of atoms while stereoisomers have the same connectivity but different spatial arrangement. |
| Are all of the following considered stereoisomers? Conformation isomer, enantiomer, and diastereomer |
| Yes. (Diastereomers are cis-trans, conformational isomers are anti/eclipse/gauche, and enantiomers are R/S) |
What type of isomers?  |
| Geometric/Diastereomers (of the Stereoisomer category) |
| What type of isomers exhibit chirality? |
| Enantiomers (Chiral isomers have the same connectivity, but are non-superimposable mirror images because of the different spatial arrangement of atoms) |
How many chiral centers are in this molecule?  |
8!  |
| Can ketones and aldehydes form structural isomers? |
| Yes For example C3H6O could be either a ketone (propan-2-one) or an aldehyde (propanal) |
| Describe the trend in boiling and melting point in the molecular weight of straight chain hydrocarbons |
| Melting point and boiling point of hydrocarbons increase with molecular weight. C1-C4 is gas, C5-C12 is liquid, and C20+ is solid. |
| Describe the trend in boiling and melting point in branched hydrocarbons (of the same molecular weight) |
| Melting point and boiling point of hydrocarbons decreases with more branching |
| What is a tertiary (3˚) carbon? |
| A carbon that is bonded to three other carbons. (There are also 1˚, 2˚, and 4˚) |
Compare the melting point and boiling point of cis-2-Butene and trans-2-Butene |
| cis-2-Butene has a higher boiling point (because of the higher polarity in the molecule, they hold tighter intermolecular forces in liquid) trans-2-Butene has a higher melting point (because of the shape they pack tighter in a solid) |
| Describe the major product of Markovnikov addition of an acid halide to an alkene |
| In the major product, the hydrogen (H) atom attaches to the carbon with fewer alkyl (C) substituents, or the larger number of hydrogen atoms. The halide (X) group becomes attached to the carbon with more alkyl substituents. |
| Would the addition of excess chlorine (Cl2) to an alkyne produce a substituted alkane or alkene? |
| Substituted alkene |
| Reduction of an alkyne to an alkane is completed through what type of reaction? |
| Hydrogenation |
| Addition of water to an alkene results in what type of functional group? |
| Alcohol |
| How does the hydroxyl (-OH) group affect the boiling point of alcohols? |
| Hydrogen bonding increases the intermolecular forces, requiring greater energy to pull apart during vaporization/evaporation. |
| Hydration of a straight-chain alkene produces what type of alcohol? |
| Secondary (2˚) alcohol E.g.) propan-2-ol |
| Adding concentrated sulfuric acid (H2SO4) to an alcohol produces what? |
| A double bond (alkene). |
| Which reducing agent is strong enough to reduce a carboxylic acid into an alcohol? Sodium tetrahydridoborate, NaBH4 Lithium tetrahydridoaluminate, LiAlH4 |
| Lithium tetrahydridoaluminate, LiAlH4 (NaBH4 is too weak an can only reduce aldehydes). |
| Treating butanoic acid with LiAlH4 would produce what molecule? |
| butanol |
| Adding an acid halide to an alcohol produces what? |
| alkyl halide |
| Adding PCC to a primary (1˚) alcohol produces what? |
| An aldehyde (PCC is a weak-ish oxidizer) |
| What is the major product when concentrated sulfuric acid (H2SO4) is added to a primary 1˚) alcohol? |
| An internal alkene (the minor product is a terminal alkene) |
| What is the product when water is added to 1-chloropropane? |
| propanol (A hydroxyl from the water replaces the halogen, with a byproduct HCl) |
| Can aldehyde functional groups hydrogen-bond amongst themselves? |
| No. (Hydrogen bonding requires a hydrogen bonded to a highly electronegative atom like N, O, or F) |
| How does the boiling point of an aldehyde compare to an alkene of a similar molecular weight? |
| The boiling point of the aldehyde is higher because of the polarity in the carbonyl carbon, resulting in dipole-dipole intermolecular interactions. |
| What has a lower boiling point? Octanal or Octanol |
| The Octanal aldehyde has a lower boiling point than the alcohol because aldehydes cannot form hydrogen bonds |
| What is the weaker oxidizing agent that will oxidize a primary (1˚) alcohol into an aldehyde and not a carboxylic acid? |
| PCC |
| Reacting an aldehyde with hydrogen in the presence of a catalyst, heat, and pressure will produce what type of molecule? |
| A primary (1˚) alcohol |
| Can ketone functional groups hydrogen-bond amongst themselves? |
| No. (Hydrogen bonding requires a hydrogen bonded to a highly electronegative atom like N, O, or F) |
| Oxidation of what type of molecule with potassium dichromate (K2Cr2O7) produces a ketone? |
| A secondary (2˚) alcohol |
Explain why this molecule cannot be oxidized  |
| Tertiary (3˚) alcohols be oxidized to produce a ketones since oxidation from the alcohol would make a double bond, and there is no space for additional bonds on the central carbon atom. |
| Treating a ketone with a reducing agent (like LAH or NaBH4) produces what type of molecule? |
| A secondary (2˚) alcohol |
| Hydrogenation of a ketone with Hg and an acid produces what type of molecule? |
| An alkane |
| Treating a carboxylic acid with a reducing agent (LAH) produces what type of molecule? |
| Alcohol |
| Treating an aldehyde or 1˚ alcohol with KMnO4 will make what type of molecule? |
| Carboxylic acid |
| How does the boiling point of a carboxylic acid compare to an aldehyde (of a similar molecular weight)? |
| Carboxylic acid has a higher b.p. |
| How does the boiling point of a carboxylic acid compare to an alcohol (of a similar molecular weight)? |
| Carboxylic acid has a higher b.p. |
| What is the proper name of acetic acid? |
| This carboxylic acid (CH3COOH) is called ethanoic acid |
| What is one of the main sensory characteristics of esters? |
| Smell (Different ester molecules have a wide range of characteristic odours.) |
| Reduction of an ester with LAH produces what type of molecule? |
| A primary alcohol |
| What does the following combination produce? Ethanol + Butanoic Acid |
| Ester Ethyl butanoate  |
| What is the general type of reaction between Ethanol + Butanoic Acid called? |
| Condensation reaction (condensation between a hydroxyl, OH and a hydrogen, H) |
| Saponification of esters in the presence of NaOH and heat produces what two general products? |
| Soap and alcohol |
| Hydrolysis of an ester produces what two molecules? |
| Carboxylic acid + alcohol |
| Can ether functional groups hydrogen-bond amongst themselves? |
| No. (Hydrogen bonding requires a hydrogen bonded to a highly electronegative atom like N, O, or F) |
| Compare the boiling point between an ether and an alkane with an equivalent molecular weight. |
| The boiling point of the alkane is lower than the ether because the polar C-O bonds in the ether cause greater intermolecular forces and higher boiling points in ethers. |
| Ethers can be formed in the presence of concentrated sulfuric acid (H2SO4) and two molecules of what? |
| Alcohol. This is a condensation reaction between a hydroxyl, OH group from one alcohol and a hydrogen, H from another alcohol |
Is this amine 1˚, 2˚, or 3˚? |
| 2˚ |
| What type of amine cannot form hydrogen bonds with itself? |
| 3˚ amines (Both 1˚ and 2˚ amines can form hydrogen bonds) |
| Which has the highest boiling point, an amine or alcohol (of similar molecular weight)? |
| The alcohol has the higher boiling point because the OH hydrogen bonding in alcohols is stronger than the NH hydrogen bonding in amines. |
| Treating an alkyl halide with ammonia in the presence of NaOH produces what type of molecule? |
| Amine |
| Can amides form hydrogen bonds with other amides? |
| Yes. (The N-H can hydrogen bond) |
| What is the name of reaction between an amide and carboxylic acid? |
| Condensation reaction |
| Combining what two functional groups can synthesize amides? |
| Combining (secondary) amines and carboxylic acids. |
| Hydrolysis of an amide yields what functional group products? |
| Carboxylic acid + amine |
| Reduction of an amide (with LAH) will yield what functional group? |
| Amine |
| Reacting an ester and ammonia will yield what two functional groups as products? |
| Alcohol + Amide |
| What is an aromatic molecule? |
| An unsaturated ring structure with alternating double bonds. |
| Does an aromatic ring have to contain 6 carbon atoms? |
| No, the ring could contain 10 carbons, or any combination of (4n + 2 carbons, or pi electrons) |
| What does a molecule of phenol look like? |
 |
| Are the following compounds all aromatic? Aniline, Toluene, Phenol. |
| Yes, monosubstituted benzene rings are still aromatic. |
| Does a benzene ring have the same structure as a phenyl group? |
| No, when a benzene ring is a substituent it is called a phenyl group. The phenyl group has one less hydrogen atom than benzene because it must bond to the main molecule at this position. |
| Are all carbohydrates polymers? |
| No. While most carbohydrates are polymers of several monosaccharides, technically glucose (a monosaccharide) is a carbohydrate. |
| Carbohydrates are polymers of monosaccharides, called polysaccharides. What is the polymer of protein called? What are the subunits of protein? |
| The polymer of protein is the polypeptide. The subunits are amino acids. |
| What type of reaction joins two glucose monosaccharides? |
| Condensation (between adjacent hydroxide groups) |
| What type of reaction joins two amino acid monosaccharides? |
| Condensation (between adjacent amine and carboxylic acid groups) |
| What type of bond joins two amino acid monosaccharides? |
| Peptide bond |
| Can amino acids be acidic or alkaline? |
| Yes |
| Can amino acids be hydrophilic or hydrophobic? |
| Yes |
| What causes the primary structure of polypeptides to form secondary structures? |
| Hydrogen bond interactions between the amino acids in the polypeptide |
Structure and Properties of Matter
Atomic Structure
The region around an atom where an electron is most likely to be found is called an energy level.
Solution
The energy levels are discrete energetic regions where electrons are located, with a high probability.
The Aufbau Principle
Electrons fill orbitals in the following order: 1s 2s 2p 3s 3p 3d 4s 4p 4d 4f 5s 5p 5d 5f ...
Solution
Aufbau Principle:
Electrons are placed in the lowest energy subshell available. Orbitals hold up to two electrons. Electrons must occupy each orbital of a subshell before being paired up.
Electrons fill in the following order: 1s 2s 2p 3s 3p 4s 3d 4p 5s 4d 5p 6s 4f 5d 6p 7s 5f 6d ...

Electrons are placed in the lowest energy subshell available. Orbitals hold up to two electrons. Electrons must occupy each orbital of a subshell before being paired up.
Electrons fill in the following order: 1s 2s 2p 3s 3p 4s 3d 4p 5s 4d 5p 6s 4f 5d 6p 7s 5f 6d ...

The highest energy sublevel in a Titanium, Ti atom is:
Solution
Electrons fill in the following order of sublevels from low to high energy: 1s 2s 2p 3s 3p 4s 3d 4p 5s 4d 5p 6s 4f 5d 6p 7s 5f 6d ...
Aufbau principle - fills lower energy sublevels first. Notice the 3d sublevel has higher energy than the 4s because it is filled after 4s, despite being a lower energy level, n.

Aufbau principle - fills lower energy sublevels first. Notice the 3d sublevel has higher energy than the 4s because it is filled after 4s, despite being a lower energy level, n.

Electron Configurations
The shorthand, ground state electron configuration for Silicon is [Ne] 3s24p2
Solution
The shorthand, ground state electron configuration for Silicon is [Ne] 3s23p2
Electron Configurations: Half-filled d Orbital
The ground-state electron configuration 1s2 2s2 2p 6 3s2 3p 6 4s1 3d5 is for the element...
Solution
Chromium (Cr) takes this configuration because there is extra stability from the half-filled d orbital.
This occurs with the other elements in the same group: Molybdenum (Mo) and Tungsten (W).
(The 6 elements with unexpected configurations are Cu, Ag, Au, and Cr, Mo, W).
This occurs with the other elements in the same group: Molybdenum (Mo) and Tungsten (W).
(The 6 elements with unexpected configurations are Cu, Ag, Au, and Cr, Mo, W).
Electron Configurations: s Vs. d Orbital
The ground state electron configuration for Copper is
Solution
This same thing occurs for the other elements in the same group as Copper (Cu): Silver (Ag) and Gold (Au).
The expected configuration: 4s2 3d9
The actual, more stable configuration: 4s1 3d10
The valence electrons are more stable when the s sublevel is half full and the d sublevel is full.
The expected configuration: 4s2 3d9
The actual, more stable configuration: 4s1 3d10
The valence electrons are more stable when the s sublevel is half full and the d sublevel is full.
Electron Configurations: Transition Metal Ions
The Iron atom Fe3+ is formed by when iron loses
Solution
Video
Iron is multivalent, most common is Fe3+. Ground state iron has 6 electrons in the 3d shell, and 2 electrons in the 4s.
The higher energy 3d loses 1 electron, to become half full. The lower energy 4s loses both electrons to become empty.
1s22s22p63s23p64s23d6
...
1s22s22p63s23p64s03d5 = 1s22s22p63s23p63d5
Writing 4s2 before 3d6 follows the Aufbau principle order, however some other sources show the other way with 3d before 4s.
The higher energy 3d loses 1 electron, to become half full. The lower energy 4s loses both electrons to become empty.
1s22s22p63s23p64s23d6 ... 1s22s22p63s23p6
Sublevels and Orbitals
The p sublevel contains how many orbitals?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
There are 3 orbitals in the 'p' sublevel. (1 orbital in the 's' sublevel, and 5 orbitals in the 'd' sublevel).
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Orbital
One orbital can not have which of the following?
Solution
One orbital can hold up to 2 electrons with opposite spins. They can be empty, with zero electrons. Note that orbitals should not be confused with 'octet'.
'
Electron Configuration: Orbitals
The number of orbitals in the 3rd energy level is
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Number of orbitals = (n energy level)2 = (3)2 = 9
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Rutherford's Gold Foil Experiment
Ernest Rutherford's observations of alpha particle deflection from gold foil allowed him to conclude that the nucleus was a large proportion of the atom.
Solution
The reflection of any alpha particles at all was surprising proof that the atom did contain something inside it.
However, only a small number of alpha particles were deflected, so the atom was mostly empty space with a very small nucleus. The large majority of an atom is the electron cloud. Rutherford coins the term 'proton' in 1914.
However, only a small number of alpha particles were deflected, so the atom was mostly empty space with a very small nucleus. The large majority of an atom is the electron cloud. Rutherford coins the term 'proton' in 1914.
Geiger–Marsden (Rutherford's) Gold Foil Experiment
If Thomsons's atomic model (1897) was correct, Rutherford would have observed which of the following during the gold foil experiment?
Solution
Thompson's model spaced the negatively charged particles evenly throughout a positively charged substance in the atom, like a "plum pudding", or chocolate chips in a cookie. The alpha particles need a mass like a nucleus to reflect, and would not be reflected from these tiny, lone subatomic particles in Thomson's model.
The Photoelectric Effect
The photoelectric effect is one of the experiments that demonstrates light behaves not just as waves, but as particles too.
Solution
Light clearly behaves as electromagnetic waves, and the photoelectric effect shows that light behaves is discreet quanta of energy as photons or particles. The experiment involved shining light at a certain frequency on a metal to cause electrons to be released. Although Hertz did this experiment in 1887, it was Einstein who used it in 1905 to explain the quantum (packet) energy of light depends on its frequency. Einstein later won the Nobel Prize for this explanation in 1921.
Isotopes and Mass Spectrometer
A mass spectrometer measures the
Solution
A mass spectrometer accelerates the particles (charges) through a uniform magnetic field, and the amount of deflection or curvature indicates the mass.
Different masses of ions were explained by different numbers of neutrons: isotopes!
Different masses of ions were explained by different numbers of neutrons: isotopes!
Isotopes and Mass Spectrometer
Heavier isotopes are deflected more than lighter isotopes in a mass spectrometer.
Solution
A mass spectrometer accelerates the particles (charges) through a uniform magnetic field, and the amount of deflection or curvature indicates the mass.
Heavier isotopes are deflected less in a mass spectrometer. Their radius of curvature is larger.
Heavier isotopes are deflected less in a mass spectrometer. Their radius of curvature is larger.
Bohr Theory
Bohr's theory of atomic structure was based on the idea that electrons orbit the nucleus on energy levels and when discreet quanta of energy is absorbed, electrons can transition or jump to higher energy levels. Conversely when electrons return or fall back down to lower energy levels, discreet quanta of energy, called photons are released.
Solution
When discreet quanta of energy is absorbed, electrons can transition or jump to higher energy levels.
When electrons return or fall back down to lower energy levels, discreet quanta of energy, called photons are released.
The discrete quanta is based on the distance between energy levels and partly shows the existence of energy levels in atoms.
When electrons return or fall back down to lower energy levels, discreet quanta of energy, called photons are released.
The discrete quanta is based on the distance between energy levels and partly shows the existence of energy levels in atoms.
Quantum Numbers
What does the secondary quantum number represent? Solution
| Principal Quantum Number | n | Energy Level, or Shell, n = 1, 2, 3, 4... |
| Secondary, Azimuthal Quantum Number | l | Sublevel/Subshell, (0)s, (1)p, (2)d, (3)f |
| Third, Magnetic Quantum Number | ml | Orientation, _, _ _ _, _ _ _ _ _, _ _ _ _ _ _ _. |
| Fourth, Spin Quantum Number | ms | Electron Spin, +½, -½ |
Get the range of l...
±l = n-1
The second, azimuthal quantum number allows the third quantum number to be determined. For example, for
n = 1 →→ l = 0 →→ 0 →→ s sublevel
n = 2 →→ l = 0, 1 →→ -1, 0, +1 →→ p sublevel
n = 3 →→ l = 0, 1, 2 →→ -2, -1, 0, +1, +2 →→ d sublevel
S (shart), P (principal), D (diffuse), F (fundamental)... these sublevels or subshells have different shapes.
n = 1 →→ l = 0 →→ 0 →→ s sublevel
n = 2 →→ l = 0, 1 →→ -1, 0, +1 →→ p sublevel
n = 3 →→ l = 0, 1, 2 →→ -2, -1, 0, +1, +2 →→ d sublevel
S (shart), P (principal), D (diffuse), F (fundamental)... these sublevels or subshells have different shapes.
Quantum Numbers
For the principle quantum number of n = 3, which of the following are the values of secondary azimuthal, l and magnetic, ml quantum numbers, respectively?
Solution
- 1 only
- 2 only
- 3 only
- 0, or 1
- 0, or 1, or 2
- 1, or 2
- 1, or 2, or 3
- -1, 0, 1
- -2, -1, 0, 1, 2
- -3, -2, -1, 0, 1, 2, 3
Secondary quantum number, l = (n-1)
l = 3 - 1
l = 2 (l can be a maximum of 2: 0, or 1, or 2)
for the highest l = 2, then ml is from -2 --> +2
Magnetic quantum number is from -l to +l. The secondary quantum number indicates the shape of the electron orbit on subshells from the number of values for l. The magnetic quantum number is the number of orientations of orbitals that can exist. E.g.) A secondary quantum number = (1)p would have the following number of orbitals (_ _ _) according to (-1, 0, 1).
- 1 only
- 2 only
- 3 only
- 0, or 1
- 0, or 1, or 2
- 1, or 2
- 1, or 2, or 3
- -1, 0, 1
- -2, -1, 0, 1, 2
- -3, -2, -1, 0, 1, 2, 3
l = 3 - 1
l = 2 (l can be a maximum of 2: 0, or 1, or 2)
for the highest l = 2, then ml is from -2 --> +2
Magnetic quantum number is from -l to +l. The secondary quantum number indicates the shape of the electron orbit on subshells from the number of values for l. The magnetic quantum number is the number of orientations of orbitals that can exist. E.g.) A secondary quantum number = (1)p would have the following number of orbitals (_ _ _) according to (-1, 0, 1).
Quantum Numbers
An atom with the quantum numbers, n = 2 and l = 2, has 8 electrons in the shell.
Solution
The following combination of quantum numbers is not possible: n = 2 and l = 2.
The secondary, azimuthal quantum number (l) is (n-1) = 1. So n = 2 and l = 1.
(It is true that there are 8 electron in the 2s, 2p shell).
The secondary, azimuthal quantum number (l) is (n-1) = 1. So n = 2 and l = 1.
(It is true that there are 8 electron in the 2s, 2p shell).
The quantum number responsible for explaining the interaction of atoms with magnetic fields is called the magnetic quantum number, ml.
Solution
This is misleading. The magnetic quantum number actually describes the electron's orientation/location in space, with one, three, or five possible orientations according to the following positions:
ml = 0
ml = -1, 0, or 1.
ml = -2, -1, 0, 1, or 2.
It is actually the different spin of electrons (+½, -½) from the spin quantum number, m2 that explains if the atom will be attracted or repelled by a magnetic field. Paired electrons are diamagnetic and are not attracted to magnetic fields, rather slightly repelled. Unpaired electrons are paramagnetic and are attracted to magnetic fields.
ml = 0
ml = -1, 0, or 1.
ml = -2, -1, 0, 1, or 2.
It is actually the different spin of electrons (+½, -½) from the spin quantum number, m2 that explains if the atom will be attracted or repelled by a magnetic field. Paired electrons are diamagnetic and are not attracted to magnetic fields, rather slightly repelled. Unpaired electrons are paramagnetic and are attracted to magnetic fields.
Which of the following symbols corresponds to the quantum numbers: n = 2, l = 1?
Solution
The principal quantum number (n)
The second, azimuthal quantum number (l)
The third, magnetic quantum number (ml)
The fourth, spin quantum number (ms).
n = 2 → this tells us it's in the 2nd energy level.
l = 1 → this tells us the number of orbitals in the sublevel from -l to +l, which would be -1, 0, +1 → which is 3 orbitals → the p sublevel has 3 orbitals.
The second, azimuthal quantum number (l)
The third, magnetic quantum number (ml)
The fourth, spin quantum number (ms).
n = 2 → this tells us it's in the 2nd energy level.
l = 1 → this tells us the number of orbitals in the sublevel from -l to +l, which would be -1, 0, +1 → which is 3 orbitals → the p sublevel has 3 orbitals.
State the maximum number of electrons in an atom that can have the following quantum numbers in total in all principle quantum rows (n) and any sublevel: n = 2, ml = 0.
Solution
Using the first quantum number (n = 2), there are 2 azimuthal values (l) from 0 to (n-1): 0, 1
The two azimuthal values are written from -l to +l, giving us the number of orbitals in a sublevel:
0 = 1 orbital in s
-1, 0, +1 = 3 orbitals in s.
2s has 2e- with Ml = 0
2p has 2e- with Ml = 0.
2e- + 2e- = 4e-
Think of this like a notation for each orbital containing electrons:
- n = 2, l = 0, ml = 0
- n = 2, l = 1, ml = -1
- n = 2, l = 1, ml = 0
- n = 2, l = 1, ml = +1
See that there are 4 possible combinations, with 2 ml values.
(Note that we don't count the n=1 sublevel 1s, which has a ml=0
The two azimuthal values are written from -l to +l, giving us the number of orbitals in a sublevel:
0 = 1 orbital in s
-1, 0, +1 = 3 orbitals in s.
2s has 2e- with Ml = 0
2p has 2e- with Ml = 0.
2e- + 2e- = 4e-
Think of this like a notation for each orbital containing electrons:
- n = 2, l = 0, ml = 0
- n = 2, l = 1, ml = -1
- n = 2, l = 1, ml = 0
- n = 2, l = 1, ml = +1
(Note that we don't count the n=1 sublevel 1s, which has a ml=0
Quantum Numbers: f-block
The f sublevel has 7 orbitals and the d sublevel can hold 10 electrons.
Solution
True, the f sublevel has 7 orbitals and the d sublevel can hold 10 electrons.
What energy levels are the f-blocks in? [2]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
4-f & 5-f
(Not 6 & 7 as many people think)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(Not 6 & 7 as many people think)
Pauli Exclusion Principle
Two electrons in the same orbital have the same spin directions.
Solution
Wolfgang Pauli, Austrian physicist (1900-1958). The Pauli exclusion principle states that no two electrons in an atom have the same four quantum numbers: principle n, secondary l, magnetic ml, and spin ms.
Hund's Rule
The 2p subshell in an oxygen atom contains the following electron configuration
Solution
Each of the three orbitals must fill with at least one electron before the electrons begin to pair up.
An orbital can hold up to 8 electrons
Solution
An orbital can only hold up to 2 electrons. Orbitals are not to be confused with subshells, which contain orbitals, and have the same values of n and l, e.g. 2s, 3p...
Heisenberg's uncertainty principle
"The more precisely the position [of a subatomic particle] is determined, the less precisely the ____________ is known in this instant, and vice versa."
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
"The more precisely the position [of a subatomic particle] is determined, the less precisely the momentum is known in this instant, and vice versa." -Heisenberg
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Max Planck's Explanation of Blackbody Radiation
Max Planck's experiments with blackbodies (perfectly black objects that emit, rather than reflect light) showed that energy of atoms in solids are not quantized, rather the energy is continuous.
Solution
The experiment(s) showed that energy of atoms in solids are quantized, and not continuous.
The spectrum curves appear continuous when presented on a simple line graph, but this line actually misrepresents the very small differences in discreet, quantized energies. These 'quanta' of light energy are photon particles.
The spectrum curves appear continuous when presented on a simple line graph, but this line actually misrepresents the very small differences in discreet, quantized energies. These 'quanta' of light energy are photon particles.
Electronegativity
Which of the following covalent bonds has the highest polarity?
Solution
Oxygen has the highest electronegativity of all the elements included here. Therefore the electronegativity difference with hydrogen will be highest, giving the O-H bond the highest polarity.
Hydrogen Bonding
Hydrogen bonding is possible whenever a molecule contains hydrogen bonds
Solution
Hydrogen bonding is possible whenever the molecule contains hydrogen atoms bonded to N, O, and F atoms
Central Atoms
In addition to carbon, sulfur and phosphorus can act as central atoms in a compound.
Solution
And they can form more than an octet on the central atom: SF6 and PCl5
Bonding and Electron Configurations
Determine the compound that will form by combining an element that has the electron configuration [Ne]3s2, plus Oxygen.
Solution
[Ne]3s2 is Magnesium, Mg and forms a Mg2+ cation because it is in group two and can easily donate the two electrons to become isoelectronic with the noble gas Neon.
Oxygen forms an O2- anion because it is in group 6A (16) and can easily gain two more electrons to get a full octet.
The net charges are balanced in the electron transfer: Mg2+O2-
Since the charges are balanced, the compound takes one of each cation and anion: MgO.
Oxygen forms an O2- anion because it is in group 6A (16) and can easily gain two more electrons to get a full octet.
The net charges are balanced in the electron transfer: Mg2+O2-
Since the charges are balanced, the compound takes one of each cation and anion: MgO.
Lewis Diagram
The Lewis structure of an atom with the electron configuration 1s22s22p63s23p4 would have
Solution
One pair in the 3s sublevel, one pair and two unpaired in the 3p sublevel.
Lewis Diagram
The lewis structure of a molecule of carbon dioxide, CO2 would display how many total electrons?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
CO2 has 4 valence electrons in carbon, and 6 valence electrons in each oxygen.
4 + 6 + 6 = 16.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
4 + 6 + 6 = 16.
Lewis Diagram for Ions
A lewis structure for the Scandium ion, Sc3+ would contain how many electrons?
Solution
The scandium has given away three electrons to become the Sc3+ ion, leaving the valence shell with zero electrons remaining.
Lewis Diagrams for Ionic Compounds
Draw lewis diagrams for the following molecules
NaCl
Solution


MgBr2
Solution


Li2S
Solution


CaO
Solution


Lewis Diagrams for Covalent Compounds with Single Bonds
Draw lewis diagrams for the following molecules using the rules below:
| Step | What to Do |
| 1 | Arrange the atoms with the element that forms most bonds in the central position. |
| 2 | Add the total number of valence electrons. |
| 3 | Start by placing one bonding pair of electrons between each atom. |
| 4 | Put remaining electrons as lone pairs on all atoms except central atom, to a maximum octet of 8 electrons per atom. |
| 5 | If octet on central atom is incomplete, move peripheral lone pairs into bonding electrons that are shared with the central atom. |
| 6 | Make sure central and peripheral atoms have complete octets. Now if there are extra electrons, place these as lone pairs on the central atom (*exception to octet rule). |
NF3
Solution
Trigonal pyramidal (a.k.a. Pyramidal)


H2S
Solution
Video
Bent (this is not linear because the two lone pairs will bend the molecule in 3D space due to the high repulsion).


CH3Cl
Solution
Tetrahedral


C2H6
Solution


PCl3
Solution
Trigonal pyramidal (a.k.a. Pyramidal)


Lewis Diagrams for Charged Compounds
Draw lewis diagrams for the following molecules
H3O+
Solution
Trigonal pyramidal.


NH4+
Solution
Tetrahedral


NO3-
Solution
Trigonal planar


CO32-
Solution
Trigonal planar


SO42-
Solution
Tetrahedral (many dative bonds)


HCO3-
Solution
Trigonal planar


Lewis Diagrams for Covalent Compounds with Double or Triple Bonds
Draw lewis diagrams for the following molecules
O2
Solution
Linear


P2H2
Solution


C3H6
Solution


C2F2
Solution
Linear


SO2
Solution
V-shaped


HCN
Solution
Linear


N2O
Solution
Linear


Lewis Diagrams for Covalent Compounds with Exceptions to the Octet Rule
Draw lewis diagrams for the following molecules
BF3
Solution
Trigonal planar (like BI3, BCl3, BBr3, BH3...)


SO3
Solution
Trigonal Planar


XeF4
Solution
Square Planar


H2SO4
Solution
Tetrahedral


PI5
Solution
Trigonal Bipyramidal


SF6
Solution
Octahedral


Using Orbitals to Explain Bonding Exceptions
Explain how SF6 can have 12 electrons around the central Sulfur. Use orbitals in your explanation, and determine all the different bond angles. [3]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
This hybridizes to sp3d2, or one in 's' three in 'p' and 2 in 'd'.
This creates space for 6 bonds with each of the unpaired electrons.
The different bond angles are: 90˚, 120˚, and 180˚.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
This creates space for 6 bonds with each of the unpaired electrons.
The different bond angles are: 90˚, 120˚, and 180˚.
VSEPR Shapes
The molecular geometry of the NH3 molecule is predicted by VSEPR to be...
Solution
See the 3D shape is Trigonal Pyramidal... A pyramid with a three-sided base
 It doesn't matter if it's drawn 2-dimensionally...
It doesn't matter if it's drawn 2-dimensionally...
 (Note that the 'electron group geometry' is tetrahedral).
(Note that the 'electron group geometry' is tetrahedral).
 It doesn't matter if it's drawn 2-dimensionally...
It doesn't matter if it's drawn 2-dimensionally...
 (Note that the 'electron group geometry' is tetrahedral).
(Note that the 'electron group geometry' is tetrahedral).
NF3 is trigonal pyramidal, while BF3 is trigonal planar. Use your understanding of Lewis diagrams and VSEPR theory to briefly explain. [2]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Think about what causes the differences in molecular geometries
Nitrogen has 5 valence electrons, and forms 3 covalent bond plus one lone pair. The lone pair of electrons in NF3 repels the three fluorine atoms downwards, to create the trigonal pyramidal molecule geometry with ~107˚ bond angles.
Boron has 3 valence electrons, and forms 3 covalent bonds, with no lone pair. The three identical fluorine atoms arrange themselves furthest apart in space, forming 120˚ bond angles.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Think about what causes the differences in molecular geometries
Boron has 3 valence electrons, and forms 3 covalent bonds, with no lone pair. The three identical fluorine atoms arrange themselves furthest apart in space, forming 120˚ bond angles.
VSEPR Theory
The VSEPR shape of a molecule with 2 lone pairs and 2 bonding pairs is called, Linear.
Solution
This molecule is V-shaped.
VSEPR Theory
Predict the molecular geometry (not electron pair arrangement) and state the polarity for the following compounds. Make a sketch in your own notes, if it helps.
BH3
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Trigonal Planar, Non-polar
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
PCl3
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Trigonal Pyramidal, Polar
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
H2O
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Bent (V-shaped), Polar
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
CO2
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Linear, Non-polar
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
SiH4
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Tetrahedral, Non-polar
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
PF5 (Extended)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Trigonal Bipyramidal, Non-polar
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Valence Bond Theory
Fill in the blank: Two _________ orbitals overlap to form a bonding orbital, that contains a maximum of two electrons.
Hybridization
Show with a series of sketches, how the orbitals in the s and p subshells combine to form hybridized bonding orbitals between one carbon atom and four hydrogen atoms.
Hybridization
How many pi bonds are found at the central carbon atom in carbon dioxide, CO2?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The central carbon has 2 sigma bonds, and 2 pi bonds, with a total of 4 bonding-pairs of electrons.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
One s orbital and two pairs of p orbitals overlapping creates a triple bond.
Solution
Ethyne is an example where this occurs in the C-C bond.
Dipole Polarity of Molecules
Determine the polarity (polar or non-polar) of the following molecules.
HCl
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
polar
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
BH3
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
non-polar
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
NH3
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
polar
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
O2
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
non-polar
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
CH4
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
non-polar
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
CH3Cl
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
polar
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
HO
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
polar
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Molecular Forces
Which of the following is the strongest intermolecular force?
Solution
Hydrogen Bonding is the strongest
The van der Waals intermolecular force is composed of two forces: dipole-dipole and London.
Solution
True
Increasing the number of electrons would increase the London force
Solution
London forces are caused by the attraction of the electrons from one molecule to the positive centre in an adjacent molecule. So, the strength of the London force is directly proportional to the number of electrons (and/or protons) in the molecule(s).
Molecular Forces
Describe the following types of intermolecular forces.
London Dispersion. [2]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
London Dispersion is the weakest intermolecular force, which is temporary and induced by dipole moments. These forces exist in both polar and non-polar molecules. While polar molecules have many different types of forces, non-polar molecules only have London dispersion forces.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hydrogen Bonding. [2]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hydrogen Bonding is the strongest intermolecular force. These forces exist mostly in polar molecules (but there are exceptions). The force itself is polar. Only hydrogens bonded to Nitrogen, Oxygen, or Fluorine can form hydrogen bonds with other electronegative atoms. Hydrogen bonds are not actually bonds, rather they are more of an attraction.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Molecular Forces: Physical Properties
Order the following compounds from high to low boiling point.
Solution
C5H8
C4H10
C2H6
C3H4
C5H12
Melting and boiling point is proportional to the molecular weight (g/mol) of the molecule if all functional groups are the same. Each of the given compounds are just simple hydrocarbons with the same intermolecular forces, so only the molecular weight is compared. The London dispersion intermolecular force is too weak to cause any significant increase in boiling point.
C5H8
C4H10
C2H6
C3H4
C5H12
Use your understanding of polarity, molecular forces, and molecular mass to determine which compound will have the lowest melting point.
Solution
The weakest force is non-polar London forces. This is in the non-polar CO2 and CH4 molecules. Between these two CH4 has the lower melting point because it is lighter (lower molecular mass, g/mol): 16.04g/mol compared to 44.01g/mol for the CO2.
Explain the types of intermolecular forces in the following molecule, and why there is a difference in the boiling points. Solution
| Molecule | Boiling Point (˚C) |
| Nitrogen, N2 | -195.8 ˚C |
| Carbon Monoxide, CO | -191.5 ˚C |
Iso-electronic species, meaning same number of electrons. Comparing the intermolecular forces, non-polar nitrogen has London, and polar carbon monoxide has van der Waals (London + Dipole). The stronger van der Waals forces causes the molecules to be more attracted to one another and it is harder for the molecules to split apart as the phase changes from liquid to a gas - hence the higher boiling point for carbon monoxide.
Explain how water travels up thin glass tubes (capillary action) using the terms cohesion and adhesion.
Solution
- Molecules stick to themselves in cohesion
- Molecules stick to something else in adhesion
- For thin tubes with low surface area, the adhesion is greater than the cohesion in water. The intermolecular force between the water and glass pulls the water up the glass by capillary action
- It is necessary to have strong intermolecular forces in the cohesion to pull the molecules upward. For example, liquid mercury metal does not undergo capillary action.
- Molecules stick to themselves in cohesion
- Molecules stick to something else in adhesion
- For thin tubes with low surface area, the adhesion is greater than the cohesion in water. The intermolecular force between the water and glass pulls the water up the glass by capillary action
- It is necessary to have strong intermolecular forces in the cohesion to pull the molecules upward. For example, liquid mercury metal does not undergo capillary action.
Explain how a safety pin floats on the surface of water when placed horizontally, but sinks when placed vertically, using the terms cohesion and adhesion.
Solution
- The surface tension of the water is due to cohesion (sticking of the water molecules amongst themselves)
- If the mass of the safety pin is low and the surface area in contact with the water molecules is high, then the pin will be supported by the strong cohesion of the water molecules underneath
- When the pressure of the pin is increased by placing it vertically, the weight is great enough to separate the cohesion intermolecular force between the water molecules and the pin pulls apart the water molecules to fall and sink
- The surface tension of the water is due to cohesion (sticking of the water molecules amongst themselves)
- If the mass of the safety pin is low and the surface area in contact with the water molecules is high, then the pin will be supported by the strong cohesion of the water molecules underneath
- When the pressure of the pin is increased by placing it vertically, the weight is great enough to separate the cohesion intermolecular force between the water molecules and the pin pulls apart the water molecules to fall and sink
Electrolytes
Which of the following can conduct electricity in either a solid, liquid, gaseous, or aqueous state? (More than one answer: check all that apply)
Solution
Metallic elements can conduct in the solid and liquid phase (like copper wire, or molten gold), while ionic can conduct only when in the aqueous state (like electrolytes, e.g. saltwater).
Crystal Structure
Describe the relation between the lattice and the unit cell. [2]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
- There are many different types of unit cells (over 14), that are the smallest repeating unit, which combine to form the organized lattice grid structure.
- The atoms are arranged on the lattice points, in various configurations, forming various crystal structures.
- Pure crystals are made of these lattice arrangements.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
- There are many different types of unit cells (over 14), that are the smallest repeating unit, which combine to form the organized lattice grid structure.
- The atoms are arranged on the lattice points, in various configurations, forming various crystal structures.
- Pure crystals are made of these lattice arrangements.
Classify the type of unit cell below.
Solution
This is a face-centered cubic.
Classify the type of unit cell below.
Solution
This is a body-centered cubic.
Physical Properties of Ionic Crystals
State at least one physical property of ionic crystals. [1] Solution
_onder_de_microscoop_creativeCommons.jpg) |
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Some physical properties
- High melting and boiling point because of the ionic bonds
- Crystals are brittle and hard
- The solid crystals do not conduct electricity (unless molten liquid, or dissolved as aqueous)
Metallic Crystals
What property of metallic crystals forms the bond and also allows these crystals to conduct electricity?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The answer is looking for:
- The "sea of electrons" or "delocalized electrons"
These negatively charged electrons form the bond between the nuclei and also propagate any current through the material.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
- The "sea of electrons" or "delocalized electrons"
Metal Crystals
All natural and processed metals exist in a single crystal form.
Solution
False. You might think this because of the densely packed atomic structure of metals, but the malleability of metals allows the metal to be compact, without being a single crystal.
You can make metal crystals though the process of repeatedly heating and cooling... Crystals are typically stronger structures. In nature, crystals are occasionally formed, but more slowly over hundreds or millions of years.
You can make metal crystals though the process of repeatedly heating and cooling... Crystals are typically stronger structures. In nature, crystals are occasionally formed, but more slowly over hundreds or millions of years.
Strength of Metal Crystals
Determine the most significant factor contributing to the strength of pure, elemental metallic crystals.
Solution
The positively charged nucleus and the negatively charged sea of electrons is the basis for the strength of atomic bonding. Elements with a greater nuclear charge and number of valence electrons will be stronger and have higher boiling/melting points.
Note that the metal with the greatest atomic mass doesn't necessarily have the strongest bonds because you have to take into account the atomic radius; greater distances reduce the net force due to inner electrons shielding the outer...
Note that the metal with the greatest atomic mass doesn't necessarily have the strongest bonds because you have to take into account the atomic radius; greater distances reduce the net force due to inner electrons shielding the outer...
Types of Crystals
Classify the type of crystal with the following properties...
Solution
Doesn't conduct electricity, low melting point, soft.
Molecular (covalent) compounds do not conduct electricity because there are no free electrons or charged particles. They have a relatively low melting point, and are relatively soft crystalline solids because of the weak intermolecular forces in the crystal.
There is a wide range of molecular crystal strengths from strong quartz (SiO2) to weaker sucrose sugar (C12H22O11).
There is a wide range of molecular crystal strengths from strong quartz (SiO2) to weaker sucrose sugar (C12H22O11).
Sucrose sugar crystals are what type of crystal?
Solution
Sucrose sugar is polar molecules that form molecular crystals.
Which of the following is the strongest type of crystal?
Solution
Covalent network (macromolecular - molecules with very large numbers of atoms) are the strongest because they are truly one molecule connected by covalent bonds.
Molecular Crystals
What are the possible forces within molecular crystals?
Solution
Van der Waals forces are made of induced London dispersion force and/or permanent dipole-dipole force. Basically Van der Waals is any force except for covalent and ionic. This is the most accurate
Covalent Network Solids
Covalent network crystals are ____________ electrical conductors and are ____________ in most solvents.
Solution
Covalent network crystals are poor electrical conductors and are insoluble in most solvents.
Carbon Crystals
C60 Fullerines are crystals.
Solution

Yes they are considered crystals. They are covalently bonded macromolecules that have a high boiling/melting point
Which of the following carbon-containing solid can conduct electricity?
Solution
Actually, graphite can conduct electricity due to its special form. The sp2 hybridized carbons have π bonds above and below the plane of the sheets. These π bonds overlap and form an extensive bonding network. The delocalized π electrons move freely around the sheet... conducting electricity.
Flashcards: Structure and Properties
| Who developed the most generally accepted model of the atom? |
| Niels Bohr |
| What causes emission and absorption? |
| Electrons orbit the nucleus on energy levels and when discreet quanta of energy is absorbed, electrons can transition or jump to higher energy levels. Conversely when electrons return or fall back down to lower energy levels, discreet quanta of energy is released as emission. |
| Which transition has a greater change in energy? 2 → 1 or 4 → 3 |
| 2 → 1 |
| How many energy levels are in the 24Mg atom? |
| 3 |
| Does O2- and F1- have the same number of protons? |
| No, the number of protons are always different for different elements. O2- and F1- have the same number of electrons. |
| What is the principle quantum number (n) ? |
| The energy level (shell) number |
| What is the second, azimuthal quantum number (l) ? |
| The subshell: s, p, d, or f |
| What is the third, magnetic quantum number (ml) ? |
| The specific orbital within a subshell |
| What is the fourth quantum number (ms) ? |
| The electron spin, +½ or -½ |
| What is the Pauli exclusion principle? |
| Two electrons in the same atom can never have the same 4 quantum numbers |
| What is the maximum number of electron in the first, second, and third energy levels? |
| = 2n2 = 2, 8, 18 |
| What are the possible orbitals within the p subshell? |
| p = -1 → +1 = -1, 0, +1 = 3 orbitals |
| How many valence electrons are in the atom? [Ne] 3s24p2 |
| 4 (2 in the s and 2 in the p) |
| What is Hund's rule? |
| Electrons will fill the subshell with single electrons in each orbit before forming pairs in an orbit because half-filled orbitals are stable. |
| What is Heisenberg's uncertainty principle? |
| "The more precisely the position [of a subatomic particle] is determined, the less precisely the momentum is known in this instant, and vice versa." -Heisenberg |
| What is paramagnetic and diamagnetic? |
| Paramagnetic materials have unpaired electrons in orbitals and are attracted to magnets. Diamagnetic materials have all paired electrons in orbitals and are repelled by magnets. |
| The Ca2+ cation loses electrons from what subshell/sublevel? |
| s |
| How many electrons can fit in one d sublevel? |
| 10 |
| What fills first, 4s or 3d? |
| 4s |
| What fills first, 3d or 3p? |
| 3p |
| What has a higher energy, 4s or 3d? |
| 3d (the lower energy sublevel, 4s fills first) |
| Evidence from what apparatus indicated the existence of isotopes of elements? |
| Mass spectrometer |
| Would this be paramagnetic or diamagnetic? |
| Paramagnetic |
| Determine the valence electron configuration of carbon, which has 4 valence electrons |
| 2s22p2 |
| What is a sigma (σ) and a pi (π) bond? |
| A sigma bond is a single bond, a pi bond is a double bond that can only occur with the presence of a sigma bond. |
| What are the components of a triple bond? |
| 1 sigma and 2 pi bonds |
| Can some electrons have a full valence without 8 electrons? |
| Yes, hydrogen and helium have a full valence with 2 electrons |
| How does bond length compare to bond strength? |
| Shorter bonds are stronger. |
| How does bond length compare to the number of bonds? |
| More bonds are shorter in length, for example triple bonds are shorter than single bonds. |
| What type of bond would form with the following electronegativity ranges? 0 - 0.5 0.5 - 1.7 1.7 + |
| Non-polar covalent Polar covalent Ionic |
| How many total electrons are distributed in a lewis structure of NH3? |
| 8 |
| What are resonance structures? |
| Structures that differ in lone pair arrangement and bonding, but with the same relative positioning of the atoms |
| What is the bond angle in a tetrahedral arrangement? |
| 109.5˚ |
| What is the electron arrangement of a carbon dioxide molecule? |
| linear |
| What is the electron arrangement of a water molecule? |
| tetrahedral |
| What is the electron arrangement of a molecule with two single bonds, and one lone pair? |
| trigonal planar |
| What is the electron arrangement of an ammonia (NH3) molecule? |
| tetrahedral (don't forget about the lone pair) |
| What is the strongest intermolecular force? |
| Hydrogen bonding |
| How does intermolecular force affect melting and boiling point? |
| Stronger intermolecular forces have higher melting and boiling points |
Thermochemistry - Energy Changes
| Specific Topic | General Topic | School | Date |
|---|---|---|---|
| Enthalpy of Reaction ∆Hrxn | Equation | North Toronto | Nov 2013 |
| Enthalpy of Reaction ∆Hrxn | Hess's Law | North Toronto | Nov 2013 |
Pathways of Simple Chemical Reactions
Given a graph of the energy during a reaction pathway.

Which of the following represents the activation energy, Ea?
Solution
Activation energy (Ea) is the energy required for the reaction to progress from the reactants to reach the temporary intermediate state at which the molecules in rearranged and bonds are broken and new bonds start to form.
= 'A'
This energy 'hump' represents a threshold or barrier for the reaction to overcome for the reaction to proceed. Catalysts (like enzymes or certain metals) lower the activation energy and increase the rate of reaction.
Which of the following represents change in enthalpy, ∆H?
Solution
Enthalpy (∆H) is the difference in energy between the reactants and products. When products have less energy, -∆H is exothermic. When products have more energy, +∆H is endothermic. The difference between products and reactants 'C' is the enthalpy, ∆H. (Also could be A - B) In this graph it is endothermic, +∆H.
Heat Exchange
An increase in heat in a system is indicated as:
Solution
For heat in a system:
+ q is an increase,
- q is a decrease.
+ q is an increase,
- q is a decrease.
Thermochemistry: Exothermic and Endothermic
Endothermic reactions have heat on the right side of the equation
Solution
Endothermic reactions absorb heat, therefore heat is on the same side as the reactants.
In endothermic reactions
Solution
Because energy is absorbed giving the products more potential energy than the reactants.
Thermochemistry: Exothermic and Endothermic
The following reaction is exothermic.
Solution
Heat is released when the water condenses from higher energy gas to a lower energy liquid. This heat must go somewhere into the surroundings, which makes this condensation reaction exothermic.
Cold packs feel cold because they absorb heat from the surroundings and are exothermic.
Solution
Cold packs feel cold because they absorb heat from the surroundings and are endothermic.
Determine which of the following is an endothermic process.
Solution
Photosynthesis is endothermic because the plant cells gain (light) energy from the Sun.
Thermochemistry: Exothermic and Endothermic
On a potential energy diagram, the enthalpy change, ∆H is assumed to be the amount of heat released or absorbed during the reaction progress.
Solution
This is true for adiabatic reactions (constant pressure, pressure is unconstrained). Enthalpy is based on the change (∆) in heat because enthalpy cannot be measured directly, without a change.
Systems
A closed system can
Solution
It is closed to the exchange of matter only, not heat. For example, hot and cold packs can exchange heat, but not matter.
In isolated system cannot exchange matter nor energy with the surroundings.
Solution
Think of an isolate system like a closed system that has perfect insulation, and therefore does not exchange heat.
(Contrast that with an open system, which allows the transfer of both matter and energy with the surroundings).
(Contrast that with an open system, which allows the transfer of both matter and energy with the surroundings).
Which of the following is an example of an isolated system?
Solution
Isolated systems have no change of mass or heat. Only the vacuum chamber has absolutely no change in either.
Definition of Specific Heat
Specific heat is defined as
Solution
The energy required to raise the temperature of one gram by 1˚C
(Note that this is the same as raising the temperature of one gram by 1 Kelvin since ∆˚C = ∆K)
(Note that this is the same as raising the temperature of one gram by 1 Kelvin since ∆˚C = ∆K)
Specific Heat Capacity Theory
The international standard units of specific heat capacity are:
Solution
J/(g·˚C)
(and sometimes stated as J/kg·˚C).
(and sometimes stated as J/kg·˚C).
Specific Heat Theory
What unit of temperature is used for the change in temperature in the equation q = m c ∆T?
Solution
- Kelvin
- Celsius
- Joules
- Calories
The magnitude of the change (∆) in temperature (∆T) would be the same for a change in Kelvin or degrees Celsius. For example +100K = +100˚C
- Kelvin
- Celsius
- Joules
- Calories
What unit of energy is used for heat in the equation q = m c ∆T.
Solution
- Kelvin
- Celsius
- Joules
- Calories
The Joule is a unit of heat, and energy.
- Kelvin
- Celsius
- Joules
- Calories
Calorimetry
A calorimeter measures
Solution
A calorimeter is a device used to measure changes in heat in chemical and physical reactions.
Processes
Isobaric means constant pressure, and adiabatic means no heat exchange.
Solution
'Iso' means equal and bar is a unit of pressure, so iso-baric means equal pressure.
Adiabatic systems do not exchange heat.
Adiabatic systems do not exchange heat.
Specific Heat
If the specific heat of aluminum is 2.01 J/(g·˚C), how much heat is required to raise the temperature of 2 g by 1˚C?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
J
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
J
Hint Unavailable
Specific Heat: q = m c ∆T
100 J of heat is added to a 25 g unknown block at 5.45˚C causing the block to heat to 10.00˚C. Determine the identity of the unknown sample.
Solution
Specific Heat: q = nH
Calculate the heat required to vaporize 100 g of nitrogen gas at -196˚C if the enthalpy of vaporization of nitrogen is 5.56 kJ/mol
Solution
q
Hint
Clear
Info
Incorrect Attempts:
CHECK
kJ
Hint Unavailable
Molar enthalpy is given here, in kJ/mol...
q
Hint
Clear
Info
Incorrect Attempts:
CHECK
kJ
Hint Unavailable
Specific Heat, 2 Samples, Find mass: q = m c ∆T
The laboratory scale is broken and a chemist needs to figure out the mass of a known sample of pure silver. The chemist has a heat source, calorimeter, and thermometer to use so they decide to find the mass using calorimetry. Starting at room temperature, 25˚C, the sample is placed in the calorimeter and immersed in 0.45kg of water (4.18 J·g-1·˚C-1). It takes 142,875 J of heat to bring the sample to a boil at 100˚C. Given the specific heat capacity of silver is 0.240 J·g-1·˚C-1, determine the mass of the silver.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
g
Hint Unavailable
Make sure to plug in 450g for water, and not 0.45kg
Hint
Clear
Info
Incorrect Attempts:
CHECK
g
Hint Unavailable
Specific Heat, 2 Samples, Find Tf: q = m c ∆T
Equal masses of ethanol (2.46 J·g-1·˚C-1) and water (4.18 J·g-1·˚C-1) are mixed to form a 700g solution at room temperature, 298K. The solution is heated with 124,031.88 J of energy.
Total Heat Added = Heat gain in Ethanol + Heat gain in Water
Determine the final temperature of the mixture.
Solution
Tf =
Hint
Clear
Info
Incorrect Attempts:
CHECK
K
Hint Unavailable
Tf =
Hint
Clear
Info
Incorrect Attempts:
CHECK
K
Hint Unavailable
Specific Heat, 2 Samples, Find Tf Mass Ratio: q = m c ∆T
A 1,050 ˚C glowing-hot block of gold (0.129 J·g-1·˚C-1) is placed in a calorimeter filled with nothing but air (1.02 J·g-1·˚C-1) at room temperature, 298K. If the mass of gold is 5 times the mass of air, calculate the final temperature in the calorimeter assuming no heat loss.
Solution
Video
Tf =
Hint
Clear
Info
Incorrect Attempts:
CHECK
˚C
You don't need mass. Mass cancels when you set the heat of gold equal to the heat of air.
Let the mass of the air be m, and the mass of the gold be 5m.
IMPORTANT: gain in heat = +q, loss of heat = -q
Tf =
Hint
Clear
Info
Incorrect Attempts:
CHECK
˚C
You don't need mass. Mass cancels when you set the heat of gold equal to the heat of air.
IMPORTANT: gain in heat = +q, loss of heat = -q
Specific Heat With Phase Change: q = m c ∆T + mH
You want to make ice tea in the summertime by brewing a pot of 1.0 L (1.0 kg) of tea at 372K, and cooling it to the drinking temperature of 275K. You have an unlimited supply of 50 g ice cubes at 263K. Determine the number of ice cubes to bring the ice tea to the perfect temperature. (cwater = 4.18 J·g-1·˚C-1, cice = 2.1 J·g-1·˚C-1, Hf (water) = 373 J/g)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
cubes
qtea = -(qice cube + qcube phase change + qcube water)
Since the tea and ice cubes reach the same temperature, the heat lost in the tea equals the heat gained in the ice cube.
Let the total mass of ice cubes be 50n (where 'n' is the number of ice cubes, and each cube is 50g)
Therefore (rounding up), 21 ice cubes are needed.
Hint
Clear
Info
Incorrect Attempts:
CHECK
cubes
qtea = -(qice cube + qcube phase change + qcube water)
Let the total mass of ice cubes be 50n (where 'n' is the number of ice cubes, and each cube is 50g) Therefore (rounding up), 21 ice cubes are needed.
Specific Heat: Propane Fridge and Liquid Nitrogen
The following values are all used in the questions below.
| boiling point N2 (l) = -196˚C |
| melting point N2 (s) = -210˚C |
| enthalpy of vaporization N2 (l), Hvap = 199 J/g |
| enthalpy of fusion N2 (l), Hfus = 25.7 J/g |
| specific heat N2 (g), c = 1.34 J/gK |
| specific heat N2 (l), c = 2.042 J/gK |
| specific heat N2 (s), c = 2 J/gK |
| boiling point NH3 (l) = -33˚C |
| enthalpy of vaporization NH3 (l), Hvap = 1,370 J/g |
| specific heat NH3 (l), c = 4.7 J/gK |
| specific heat NH3 (g), c = 1.64 J/gK |
A propane fridge uses fire to cool things down (for real!). We want to freeze 250 grams of nitrogen gas at room temperature (25˚C) into a solid at -220˚C. Calculate the total heat that must be transferred (from the nitrogen gas by the refrigerator). The nitrogen is releasing heat (exothermic), and the refrigerator is gaining this energy (endothermic).
Solution
q =
Hint
Clear
Info
Incorrect Attempts:
CHECK
J
Heat transferred out of a system is negative
The nitrogen gas must go through the 5 heat changes:
Note that (g) → (l) and (l) → (s) is exothermic, which is -∆H...
q =
Hint
Clear
Info
Incorrect Attempts:
CHECK
J
Heat transferred out of a system is negative
Propane gas combustion is used to convert NH3 (l) → NH3 (g). The ammonia is gaining energy in this process, which is endothermic. The gaseous ammonia passes through cooling fins and condenses into liquid ammonia. From here, the liquid ammonia evaporates, which ______(I)______ energy in the food in the refrigerator, which is an ______(II)______ process for the ammonia. [2]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
...the liquid ammonia evaporates which removes energy from the food in the refrigerator, which is an endothermic process.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Assuming the ammonia is at room temperature (it isn't in real life) calculate the mass of liquid ammonia to freeze the nitrogen above, if the ammonia starts at -35˚C and ends up at 20˚C.
Solution
m =
Hint
Clear
Info
Incorrect Attempts:
CHECK
g
Hint Unavailable
T1 = -35˚C, T2 = 20˚C...
From before... qtotal = -142,452 J ... which becomes +142,452 J for the ammonia (endothermic, +∆H)...
m =
Hint
Clear
Info
Incorrect Attempts:
CHECK
g
Hint Unavailable
Enthalpy
An endothermic reaction has a
Solution
Endothermic reactions have positive enthalpy change, + ∆H.


The following reaction is exothermic.
Solution
You can see this is exothermic (releases heat) because it has 802kJ of heat as a product on the righthand side of the equation.
Enthalpy and Stoichiometry
How much heat is released if 32.0 g of methane reacts with excess oxygen?
Solution
q =
Hint
Clear
Info
Incorrect Attempts:
CHECK
kJ
Hint Unavailable
Determine the molecular weight of methane: 16 g/mol.
32.0 g of methane = 2 mol.
Given the exothermic equation, 1 mol of CH4 = -890kJ
q =
Hint
Clear
Info
Incorrect Attempts:
CHECK
kJ
Hint Unavailable
32.0 g of methane = 2 mol.
Given the exothermic equation, 1 mol of CH4 = -890kJ
Standard State Enthalpy of Formation
Explain why the enthalpy of formation, Hf of O2 (g) is zero. [1]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The standard enthalpy of formation is the enthalpy to form 1.0 mol of a compound from its elements in their standard states. The diatomic form of gaseous oxygen, O2 (g), exists in the lowest energy form already. Since this is the lowest energy state and cannot be formed from lower energy constituent elements, then the enthalpy of formation starts at zero. Enthalpy of formation of all diatomic gases is zero.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Enthalpy
Given the molar heat of combustion of methane is -890 kJ/mol, calculate the enthalpy of reaction, Hrxn in the reaction given below.
Solution
Hrxn =
Hint
Clear
Info
Incorrect Attempts:
CHECK
kJ
Hint Unavailable
This reaction is a combustion reaction, the enthalpy of combustion is the enthalpy of reaction, so enthalpy (H) is negative.
Each methane combustion is -890kJ/mol.
= 3mol(-890 kJ/mol)
= -2,670 kJ
Hrxn =
Hint
Clear
Info
Incorrect Attempts:
CHECK
kJ
Hint Unavailable
Each methane combustion is -890kJ/mol.
= 3mol(-890 kJ/mol)
= -2,670 kJ
Heat of Formation Hf˚
The enthalpy of formation of a compound is equal and opposite to the enthalpy of combustion.
Solution
The enthalpy of reaction is the enthalpy of combustion, which is calculated using each of the enthalpies of formation of each compound.
Use the enthalpies of formation of each compound in the reaction to calculate the total enthalpy of reaction... using the equation:
Use the enthalpies of formation of each compound in the reaction to calculate the total enthalpy of reaction... using the equation:
Given the following information including the enthalpy of the reaction (combustion, Hc), calculate the enthalpy of formation, Hf˚ of sucrose C12H22O11 (s)
Solution
Hf˚ =
Hint
Clear
Info
Incorrect Attempts:
CHECK
kJ/mol
Hint Unavailable
Hf˚ =
Hint
Clear
Info
Incorrect Attempts:
CHECK
kJ/mol
Hint Unavailable
Calculating Enthalpy with Bond Energies and Hess' Law
Bond energy is the same magnitude and sign as enthalpy of formation.
Solution
Bond energy is usually positive because this is the energy required to break the bonds. In the form C → A + B
Enthalpy of formation is usually negative because it is the energy released when the compound is made from its constituent elements. In the form A + B → C
Enthalpy of formation is usually negative because it is the energy released when the compound is made from its constituent elements. In the form A + B → C
Hess' law basically states that the change in energy in a chemical process does not depend on the number of steps to occur.
Solution
Basically, the change in energy (enthalpy) of a target reaction does not depend on intermediate steps, and is the sum of the energy changes of all steps.
Given the reaction and the following bond energies, the enthalpy of formation of hydrofluoric acid would be calculated by which of the following generalized equations?
Solution
These are bond energies given in the form C → A + B because the compound is breaking apart and the enthalpy is positive.
Bond Energy Calculations are Reversed: Reactants - Products
Calculating Enthalpy with Bond Energies II
Given the reaction and the following bond energies, calculate the enthalpy of formation of hydrochloric acid.
Solution
Hf =
Hint
Clear
Info
Incorrect Attempts:
CHECK
kJ/mol
Hint Unavailable
You can see these are bond energies given in the form C → A + B because the compound is breaking apart and the enthalpy is positive. (Bond Energy Calculations are Reversed: Reactants - Products)
Hf =
Hint
Clear
Info
Incorrect Attempts:
CHECK
kJ/mol
Hint Unavailable
Given the reaction and the following bond energies, calculate the enthalpy change for the formation of water.
Solution
H =
Hint
Clear
Info
Incorrect Attempts:
CHECK
kJ/mol
Hint Unavailable
You can see these are bond energies given in the form C → A + B because the compound is breaking apart and the enthalpy is positive. (Bond Energy Calculations are Reversed: Reactants - Products)
H =
Hint
Clear
Info
Incorrect Attempts:
CHECK
kJ/mol
Hint Unavailable
ENTROPY
The Symbols
Explain the difference between ∆G, ∆H, ∆S and ∆G˚, ∆H˚, ∆S˚. [1]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The degree (˚) symbol in ∆G˚, ∆H˚, and ∆S˚ means standard-state conditions: 1 atm, 298 K, and 1 mol/L (if aqueous).
If there are any non-standard-state conditions (1 atm, 298 K, and 1 mol/L), then the specific values of ∆G, ∆H, and ∆S must be calculated based on the non-standard-state reaction conditions.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
If there are any non-standard-state conditions (1 atm, 298 K, and 1 mol/L), then the specific values of ∆G, ∆H, and ∆S must be calculated based on the non-standard-state reaction conditions.
The Equations
The equations for Gibbs free energy (G) and entropy (S) have the same format as enthalpy (H).
Solution
Video
True. And don't forget to multiply by the number of moles (n) if the individual formation equations get multiplied, or to switch the signs by multiplying by (-1) if the equations get reversed.
Incase you were dying to know, the generally accepted units are:
∆H˚f kJ/mol
∆H˚rxn kJ
∆S˚ J/mol·K
∆S˚rxn J/K
∆G˚ kJ/mol
∆G˚rxn kJ
Incase you were dying to know, the generally accepted units are:
| ∆H˚f | kJ/mol |
| ∆H˚rxn | kJ |
| ∆S˚ | J/mol·K |
| ∆S˚rxn | J/K |
| ∆G˚ | kJ/mol |
| ∆G˚rxn | kJ |
Gibbs Free Energy
What is Gibbs free energy?
Solution
Video
Gibbs free energy is the excess energy available from a reaction, used to do work. It is calculated by the entropy of a reaction minus the product of entropy and temperature. This is the work exchanged during a chemical reaction, between the system and surrounding. Gibbs free energy is at a minimum when the system (reaction) is at equilibrium.
Gibbs Free Energy ∆G
Match the different values of Gibbs free energy with their correct meaning.
Solution
Video
+ ∆G
- ∆G
∆G = 0
Spontaneous (Exergonic). The reaction is highly likely to occur because the conditions have enough energy.
The system is at Equilibrium. The forward and reverse reactions occur equally with the reverse reaction; no net change.
Non-spontaneous (Endergonic). At this temperature, the forward reaction will not occur, but the reverse reaction is more probable. There is not enough energy to drive the reaction forward (think endothermic).
Spontaneous (Exergonic) = - ∆G
Non-spontaneous (Endergonic) = + ∆G
Equilibrium, ∆G = 0 where ∆H = T∆S
+ ∆G
- ∆G
∆G = 0
Spontaneous (Exergonic). The reaction is highly likely to occur because the conditions have enough energy.
The system is at Equilibrium. The forward and reverse reactions occur equally with the reverse reaction; no net change.
Non-spontaneous (Endergonic). At this temperature, the forward reaction will not occur, but the reverse reaction is more probable. There is not enough energy to drive the reaction forward (think endothermic).
Non-spontaneous (Endergonic) = + ∆G
Equilibrium, ∆G = 0 where ∆H = T∆S
Gibbs Free Energy ∆G and Spontaneity
Determine whether reactions with the following conditions will be spontaneous.
Solution
-∆H, -∆S
+∆H, +∆S
-∆H, +∆S
+∆H, -∆S
Spontaneous (favorable) at any temperature
Non-spontaneous (unfavorable) at any temperature
Spontaneous at 'low' temperatures
Spontaneous at 'high' temperatures
The reactions that are spontaneous (favorable) at certain temperatures must use the Gibbs free energy equation to calculate the magnitude of temperature.
-∆H, +∆S → Spontaneous (favorable) at any temperature = -∆G
+∆H, -∆S → Non-spontaneous (unfavorable) at any temperature = +∆G
-∆H, -∆S → Spontaneous at 'low' temperatures
+∆H, +∆S → Spontaneous at 'high' temperatures
-∆H, -∆S
+∆H, +∆S
-∆H, +∆S
+∆H, -∆S
Spontaneous (favorable) at any temperature
Non-spontaneous (unfavorable) at any temperature
Spontaneous at 'low' temperatures
Spontaneous at 'high' temperatures
-∆H, +∆S → Spontaneous (favorable) at any temperature = -∆G
+∆H, -∆S → Non-spontaneous (unfavorable) at any temperature = +∆G
-∆H, -∆S → Spontaneous at 'low' temperatures
+∆H, +∆S → Spontaneous at 'high' temperatures
Laws of Thermodynamics
Know your thermodynamic laws. Fill in the blanks.
2nd Law of Thermodynamics: Entropy of the universe always ___________ during a spontaneous change.
Solution
Entropy of the universe always increases during a spontaneous change.
3rd Law of Thermodynamics: Entropy of a pure crystalline solid is ___________ at ___________ kelvin.
Solution
Entropy of a pure crystalline solid is 0 at 0 kelvin.
Entropy of Reaction
Calculate the entropy of reaction (∆S˚rxn) given the absolute entropies (∆S˚) in the table below, at SATP (298K, 1atm). Solution Video
| S˚ Carbon graphite (s) | 5.6 J/mol·K |
| S˚ Oxygen, O2(g) | 205.1 J/mol·K |
| S˚ Carbon dioxide (g) | 213.7 J/mol·K |
∆S˚rxn =
Hint
Clear
Info
Incorrect Attempts:
CHECK
J/K
Hint Unavailable
Remember the equation for entropy of reaction
Plug the data into the equation...
Therefore there is a decrease in entropy.
Entropy Situations
An increase in entropy is an increase in disorder where ∆S > 0, or (+∆S). Classify each of the following.
Which does not affect entropy?
Solution
Video
 All of these affect entropy:
All of these affect entropy:
Physical phase (s, l, g, aq), Temperature, Pressure, Volume, and Moles.
 All of these affect entropy:
All of these affect entropy:Physical phase (s, l, g, aq), Temperature, Pressure, Volume, and Moles.
Match the changes to the correct theoretical entropy change.
Solution
Increase volume of a gas from 500mL to 2.0L
Increase pressure of an inert gas from 1atm to 2atm
Increase in entropy (+∆S)
Decrease in entropy (-∆S)
Increase in entropy:
- Increase volume
- Decrease pressure
(Basically if the molecules are spread further apart, occupying more space, then there is an increase in entropy. For example increasing temperature would cause volume to increase, increasing entropy...)
Increase volume of a gas from 500mL to 2.0L
Increase pressure of an inert gas from 1atm to 2atm
Increase in entropy (+∆S)
Decrease in entropy (-∆S)
- Increase volume
- Decrease pressure
(Basically if the molecules are spread further apart, occupying more space, then there is an increase in entropy. For example increasing temperature would cause volume to increase, increasing entropy...)
Which of the following phase changes is a theoretical decrease in entropy?
Solution
Decrease in entropy (-∆S):
(higher entropy +∆S) gas > liquid > solid (lower entropy -∆S)
Decrease in entropy (-∆S) for soluble substances:
aqueous > solid
The entropies are:
- (s) → (aq) = +S
- (l) → (g) = +S
- (s) → (g) = +S
- (l) → (s) = -S
(higher entropy +∆S) gas > liquid > solid (lower entropy -∆S)
Decrease in entropy (-∆S) for soluble substances: aqueous > solid The entropies are:
- (s) → (aq) = +S
- (l) → (g) = +S
- (s) → (g) = +S
- (l) → (s) = -S
Match the changes to the correct theoretical entropy change.
Solution
2H2O → 2H2 + O2
2O(g) → O2 (g)
Increase in entropy (+∆S)
Decrease in entropy (-∆S)
Increasing the number of moles in a reaction is an increase in entropy, +S.
2H2O → 2H2 + O2
2O(g) → O2 (g)
Increase in entropy (+∆S)
Decrease in entropy (-∆S)
Molecule A has a melting point at 10˚C, and molecule B has a melting point at 35˚C. At room temperature (25˚C), which molecule would have the lower entropy?
Solution
Lower melting point = higher entropy.
Higher melting point = lower entropy.
The molecule that is has melted from a solid to a liquid has more kinetic motion in its molecules, would occupy a larger volume... and therefore would have a higher entropy.
The molecule that is still solid at room temperature would have the lower entropy. Molecule A melts first, leaving Molecule B still solid.
Higher melting point = lower entropy.
The molecule that is has melted from a solid to a liquid has more kinetic motion in its molecules, would occupy a larger volume... and therefore would have a higher entropy.
The molecule that is still solid at room temperature would have the lower entropy. Molecule A melts first, leaving Molecule B still solid.
If a chemical reaction proceeds such that 2 moles are converted into 4 moles (A + B → 4C), in a container with fixed volume, at constant temperature, then determine the change in entropy.
Solution
There would be no change in entropy over all
If the reaction occurs in a fixed volume container (cannot expand) then the increase in moles would cause an increase in pressure.
Individually the increase in moles would increase entropy, and the increase in pressure would decrease entropy. The net effect would cancel, so no net change in entropy.
If the reaction occurs in a fixed volume container (cannot expand) then the increase in moles would cause an increase in pressure.
Individually the increase in moles would increase entropy, and the increase in pressure would decrease entropy. The net effect would cancel, so no net change in entropy.
Equal amounts of a saturated (animal) fat and unsaturated (plant) fat are at room temperature. Which fat would have the higher entropy?
Solution
The fat that is melted into liquid would have a higher entropy than the fat that is still solid at room temperature. You should know that unsaturated fats (like olive oil) are liquid at room temperature, while saturated fats (like butter) are solid at room temperature. Therefore the unsaturated fat has the higher entropy.
Entropy (S)
Calculations with entropy must use what unit of temperature?
Solution
Must use Kelvin (K)
Entropy: Spontaneous and Non-spontaneous
For a non-spontaneous reaction, calculate the temperature at which the reaction will become spontaneous, given ∆H˚ = 500 kJ, and ∆S˚ = 100 J/K.
Solution
T =
Hint
Clear
Info
Incorrect Attempts:
CHECK
K
Hint Unavailable
The (instantaneous) point at which a reaction changes from non-spontaneous to spontaneous is at equilibrium where ∆G = 0
Therefore it would take a huge amount of energy (high temperature, T = 5,000 K) to make this reaction spontaneous.
T =
Hint
Clear
Info
Incorrect Attempts:
CHECK
K
Hint Unavailable
A Question with Enthalpy, Entropy, and Gibbs... The Whole Lot
Ethanol reacts with excess oxygen in a combustion reaction to produce carbon dioxide and water, both in gaseous states. Use the standard state (298 K) enthalpy of formation (Hf˚) and entropy (S˚) in the table to answer the questions.
| ∆Hf˚ (kJ/mol) | ∆S˚ (J/mol·K) | |
| C2H6O (l) | -278 | 160 |
| O2 (g) | 0 | 205 |
| CO2 (g) | -394 | 214 |
| H2O (l) | -286 | 70 |
The balanced reaction equation is...
Solution
Video
The balanced reaction is:
Calculate ∆H˚rxn.
Solution
Video
∆H˚rxn =
Hint
Clear
Info
Incorrect Attempts:
CHECK
kJ
Hint Unavailable
This is a lot of energy, it is exothermic, at 1.37 MJ.
(But as a comparison, high octane gasoline is over 5 MJ.)
∆H˚rxn =
Hint
Clear
Info
Incorrect Attempts:
CHECK
kJ
Hint Unavailable
(But as a comparison, high octane gasoline is over 5 MJ.)
Calculate ∆S˚rxn.
Solution
Video
∆S˚rxn =
Hint
Clear
Info
Incorrect Attempts:
CHECK
kJ
Hint Unavailable
∆S˚rxn =
Hint
Clear
Info
Incorrect Attempts:
CHECK
kJ
Hint Unavailable
Determine if the reaction is spontaneous at standard state temperature, 25˚C.
Solution
Video
Hint
Clear
Info
∆G˚rxn =
MJ ,
∴ the reaction is:
Incorrect Attempts:
CHECK
Hint Unavailable
25˚C = 298K
Calculate ∆G to determine if spontaneous (make sure energy units are the same)...
-∆G means the reaction, combustion of ethanol at room temperature, will be spontaneous.
Hint
Clear
Info
∆G˚rxn =
MJ ,
∴ the reaction is:
Incorrect Attempts:
CHECK
Hint Unavailable
Calculate ∆G to determine if spontaneous (make sure energy units are the same)... -∆G means the reaction, combustion of ethanol at room temperature, will be spontaneous.
Describe how diatomic gases used as reactants increases the available heat of the reaction greatly (more negative enthalpy).
Solution
Video
H2, O2, F2, Br2, I2, N2, Cl2
The diatomic gases (X2) have enthalpy of formation equal to zero (∆H˚f = 0 kJ/mol). In the equation, the enthalpy of reactants becomes positive and reduces the "exothermic-ness" of the reaction, for example...
The resulting ∆H˚rxn is largely negative and is highly exothermic. When combined with entropy in the Gibbs (∆G) equation, this results in a highly spontaneous reaction (-∆G).
In fact many rocket propellents use liquid oxygen, O2 (aka LOX) and liquid hydrogen H2 in the primary and upper stages of rocket launches.
In fact many rocket propellents use liquid oxygen, O2 (aka LOX) and liquid hydrogen H2 in the primary and upper stages of rocket launches.
Entropy of Fusion
Given the molar enthalpy of fusion and vaporization of ice and water below...
| ∆ Hfusion ice | 6 kJ/mol = 6,000 J/mol |
| ∆ Hvaporization water | 40.7 kJ/mol = 40,700 J/mol |
Determine the equation for change in entropy during a phase change (units J/K) to use in the next part below. Note that this is not the same as change in molar entropy (units J/mol·K).
Solution
Video
Determine the equation for entropy during a phase change... This occurs when the system is in equilibrium, therefore ∆ = 0...
Multiply by number of moles...
If 496.47 g of ice melts with the same change in entropy as vaporizing an unknown amount of water, calculate the mass of the water that gets vaporized. Note the melting point of water is 0˚C and the boiling point is 100˚C.
Solution
Video
m =
Hint
Clear
Info
Incorrect Attempts:
CHECK
g
Hint Unavailable
You should remember: Ice melts at 273 K, water vaporizes at 373 K, and water is 18 g/mol...
The question says they have the "same change in entropy" so set entropy of fusion equal to entropy of vaporization...
The mass of the water that gets vaporized is 100 g.
m =
Hint
Clear
Info
Incorrect Attempts:
CHECK
g
Hint Unavailable
The question says they have the "same change in entropy" so set entropy of fusion equal to entropy of vaporization... The mass of the water that gets vaporized is 100 g.
Calculate the entropy of sublimation. (Note this is not molar entropy).
Solution
Video
∆Ssub =
Hint
Clear
Info
Incorrect Attempts:
CHECK
J/K
Hint Unavailable
Sublimation is a phase change from (solid) to (gas). The entropy of the phase changes are additive...
∆Ssub =
Hint
Clear
Info
Incorrect Attempts:
CHECK
J/K
Hint Unavailable
Flashcards: Thermochemistry
| What does the symbol q represent? |
| Heat transfer |
| A hot mug of coffee is placed in a refrigerator. If the mug is -100J, then what is the heat transfer of the fridge? |
| +100J |
| What type of energy is shown on an energy diagram of exothermic and endothermic reactions? |
| Potential energy |
| What is the difference between exothermic and endothermic reactions on an energy diagram? |
| In endothermic reactions reactants have less potential energy than the products, in exothermic reactions reactants have more potential energy than the products |
| Is vaporization an exothermic or endothermic process? |
| Endothermic. The process absorbs heat as the liquid turns into a gas, cooling down the surroundings. |
| What is adiabatic? |
| No heat transfer between the system and surroundings |
| What is isothermal? |
| Constant temperature between the system and surroundings |
| What is isobaric? |
| Constant pressure between the system and surroundings |
| Distinguish between an open, closed, isolated/insulated system. |
| Open: exchange energy and matter Closed: exchange energy only Isolated/insulated: No exchange of heat nor energy |
| What is specific heat? |
| The energy required to raise the temperature of one gram by 1˚C |
| What are the units for q, m, and T in the equation: q = m c ∆T |
| q = Joules (J) m = mass (g) T = Kelvin (K) or Celsius (˚C) |
| What is the quantity, c in the equation: q = m c ∆T |
| Specific heat capacity, with standard units of J/(g·˚C) |
| What is the difference in physical property that results from different materials having different specific heat (c) capacities? |
| The materials hold different amounts of heat energy (q) per unit of mass (m) |
| - ∆H indicates what type of reaction? |
| -∆H = Exothermic reaction (+∆H = Endothermic reaction) |
| Is the reaction exothermic or endothermic? |
| Endothermic |
| What makes enthalpy of formation (H˚f) zero? |
| Enthalpy of formation (H˚f) is zero when the compound cannot be produced from lower energy building blocks, in other words if the energy of the compound is less than or equal to the energy of the starting constituents required to make the compound. An example the diatomic gases which are formed from standard state elements. |
| How is the enthalpy of reaction (∆Hr) calculated with Hess's Law? |
| Σ(∆H˚f of products) - Σ(∆H˚f of reactants) |
| If the decomposition of a reaction is +10kJ/mol, what would be the enthalpy change for the synthesis? |
| -10kJ/mol |
Kinetics - Rates of Reactions
Rates of Reaction
In most reactions, the rate of reaction tends to ___________ over time.
Solution
In most reactions, the rate of reaction tends to decrease over time (as the reactants get consumed).
Which (one) of the following does not affect the rate of a reaction?
Solution
The number of moles would only affect the amount of product produced or the equilibrium, not the rate. It's the concentration (moles ÷ volume) of the reactants that affects rate...
Rates of Reaction: Rate Constant
Which of the following would affect the value of the rate constant, k?
Solution
k only depends on the specific reaction, temperature, the presence of catalysts in the reaction, or the nature of the solvent(s).
k=Ae(-Ea/RT)
k = rate constant
A = frequency factor (constant that depends on temperature, frequency of collisions, orientation...)
e = mathematical quantity (e = 2.718...)
Ea = activation energy (in J/mol)
R = gas constant (from pV=nRT)
T = temperature (in K)
k=Ae(-Ea/RT)
k = rate constant
A = frequency factor (constant that depends on temperature, frequency of collisions, orientation...)
e = mathematical quantity (e = 2.718...)
Ea = activation energy (in J/mol)
R = gas constant (from pV=nRT)
T = temperature (in K)
Rates of Reaction
Decreasing the surface area of NaOH(aq) or HCl(aq) will increase the rate of reaction.
Solution
NaOH(aq) + HCl(aq) ↔ NaCl(s) + H2O(l)
Surface area only affects heterogeneous reactions in which some of the reactants are in different phases from one another like dissolving and reacting a solid with an aqueous compound. In this example, the reactants are both aqueous so the rate of reaction will not depend on surface area.
Collision Theory
Chemical reactions occur when particles collide with sufficient energy and orientation for bonds to be broken, and new bonds formed. Collisions that don't have enough energy, do not result in a reaction. Increasing the temperature causes a higher frequency of collisions, resulting in reactions between particles.
Solution
Increasing the temperature increases the kinetic energy (speed) of the reactant molecules. This would increase the energy of collision, as well as the frequency of collisions.
Catalysts
Two examples of common catalysts are enzyme proteins and platinum metal.
Solution
Catalysts lower the energy required for a reaction to occur -- they increase the rate of reaction and increase the yield. Enzymes are catalysts in biology. Platinum is a common catalyst in chemistry.
Catalysts and Reaction Rate
Catalysts reduce the enthalpy of the reaction, allowing the reaction to proceed more to completion.
Solution
Catalysts reduce the activation energy and not the enthalpy of a reaction. Activation energy is the energy required to rearrange the bonds in the molecule into a higher energy transition state. A catalyst reduces this energy, increasing the amount and rate of the reaction.
What is the order of a catalyst, such as an enzyme, in a rate equation?
Solution
A catalyst reduces activation energy, increasing the amount and rate of the reaction...
However, this is tricky, the addition of a catalyst is all-or-none, meaning the concentration of the catalyst does not matter like it matters for the reactants. Since a catalyst does not get used/consumed in the reaction it is considered to have no affect and is ZEROTH order, [Catalyst]0.
However, this is tricky, the addition of a catalyst is all-or-none, meaning the concentration of the catalyst does not matter like it matters for the reactants. Since a catalyst does not get used/consumed in the reaction it is considered to have no affect and is ZEROTH order, [Catalyst]0.
Reaction Rates
Increasing the surface area of the reactants in which of the following reactions would increase the reaction rate?
Solution
Increasing the surface area of the solid Sodium, Na(s) will increase the rate of reaction. For example, crushing the solid into a fine powder. Surface area affects all heterogeneous reactions, in which some of the reactants are in different phases from one another like dissolving and reacting a solid with an aqueous compound...
Determining Rates of Reaction with Molar Ratios
In the following reaction, if reactant 'A' gets used at a rate of 1.25 × 10-6 mol/(L·s), then at what rate is product 'D' formed?
Solution
2A + 3B → C + 5D
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
Hint Unavailable
Use the ratios:
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
Hint Unavailable
Orders of Reaction
The rate constant (k) affects the overall order of reaction.
Solution
The rate constant (k) does not affect the order of reaction.
The overall order of reaction in the following rate law is
Solution
r = k[A]2[B]3[C]2
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Overall reaction order is found by adding the orders of reaction (superscripts) in the rate law equation.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
For the following equation, the rate of the reaction is always r = k[A]2[B]3
Solution
2A + 3B → 2C
The orders of reaction (superscripts) in the rate law equation are determined empirically and are not always the same as the molar coefficients.
(However, if the reaction is elementary and the slow, rate-determining step, with no intermediates, then the rate equation would be based on the coefficients.)
(However, if the reaction is elementary and the slow, rate-determining step, with no intermediates, then the rate equation would be based on the coefficients.)
Orders of Reaction
If the initial concentration of 'A' is doubled, while the other concentrations are kept constant, the overall reaction rate will increase by a factor of...
Solution
r = k[A]3[B]1
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Assuming the other concentrations are kept constant, the rate of the reaction will increase by
Rate Factor:
= (concentration multiple)order
= (2)3
= 8
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
= (concentration multiple)order
= (2)3
= 8
If the order of reactant 'A' is two, then tripling the concentration of [A] would increase the overall reaction rate by how much?
Solution
r = k[A]2[B]3
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
[concentration]order
= [A]2
= [3]2
= 9
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
= [A]2
= [3]2
= 9
Determining Reaction Rate Directly
In the complete combustion of methane with excess oxygen, if 88.0 g of CO2(g) is produced in 32.4 s, what is the rate of the reaction?
Solution
CH4(g) + 2O2(g) → CO2(g) + 2H2O(g)
Hint
Clear
Info
Incorrect Attempts:
CHECK
mol/s
Hint Unavailable
= 88g ÷ 44g/mol ÷ 32.4s
= 0.062 mol/s
Hint
Clear
Info
Incorrect Attempts:
CHECK
mol/s
Hint Unavailable
= 0.062 mol/s
Rates of Reaction
The rate law equation can be predicted from the stoichiometry (coefficients) in the reaction equation.
Solution
The rate law must always be calculated experimentally. Sometimes the rate law is consistent with the stoichiometry, but this would be a coincidence because often the rate law is usually not consistent with the stoichiometry. (EXCEPT FOR THE SLOW, RATE-DETERMINING STEP, IF THERE ARE NO INTERMEDIATES...)
Rate Determining Step
The rate determining step in a reaction is always the slowest step in the theorized reaction mechanism.
Solution
The slowest reaction within the overall reaction is often many orders of magnitude slower and is the main determinant of the reaction speed, especially of all other sub-reactions occur very quickly.
Orders of Reaction
When [A] is doubled, the rate increases by a factor of 8.
When [B] is doubled, the rate does not change.
A + 2B → 3C + D
Determine the rate equation given the information for the reaction above.
Solution
rate =
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
Rate factor increase = (multiple)Order
r = k[A]3[B]0
r = k[A]3
rate =
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
r = k[A]3[B]0
r = k[A]3
Determine (the concentration of) [A] in the reaction above given the values in the table. Solution
| Rate = 0.5 × 10-6 mol/(L·s) |
| k = 4.0 × 10-5 L2/(mol2·s) |
| [B] = 0.50 mol/L |
[A] =
Hint
Clear
Info
Incorrect Attempts:
CHECK
mol/L
Hint Unavailable
Notice that we don't need [B]... this is called a 'red herring' in a question...
Propose an equation for the rate (r) of the rate-determining step in the slow-step of the reaction mechanism.
Solution
Given the overall reaction:
A + 2B → 3C + D
The rate-determining step is the slowest step out of all the different steps in the reaction mechanism.
Normally we go from the reaction to determine the order... But for the slow-step of the reaction mechanism, we can say that the order (3) is the coefficient on 'A'... 3A...
Since r = k[A]3, a rate determining step would be:
3A → product(s)
(We are not concerned with what all the other reaction mechanisms might be. Reaction mechanisms come from some reactions that cannot be completed in a single step like an elementary reaction, so sometimes overall reactions occur through several smaller 'sub-steps' or reaction mechanism steps.)
Normally we go from the reaction to determine the order... But for the slow-step of the reaction mechanism, we can say that the order (3) is the coefficient on 'A'... 3A...
Since r = k[A]3, a rate determining step would be: 3A → product(s) (We are not concerned with what all the other reaction mechanisms might be. Reaction mechanisms come from some reactions that cannot be completed in a single step like an elementary reaction, so sometimes overall reactions occur through several smaller 'sub-steps' or reaction mechanism steps.)
Rate-Determining Step
If two moles of a molecule or two different molecules are involved in the rate-determining step in the reaction mechanism, then the overall reaction is considered second order.
Solution
THIS ONLY WORKS FOR THE RATE-DETERMINING STEP. (If there aren't any intermediates)
r = k[A]2, the rate determining step would be: 2A → product(s)
or
r = k[A]1[B]1, the rate determining step would be: 1A + 1B → product(s)
r = k[A]2, the rate determining step would be: 2A → product(s)
or
r = k[A]1[B]1, the rate determining step would be: 1A + 1B → product(s)
Rates of Reaction
Rate can be calculated with the following...
Solution
For example, the rate can be in terms of concentration , volume , or mass ...
In the reaction below, AB decomposes from 5.5 mol/L at 15 seconds, to 0.83 mol/L at 60 seconds. Calculate the average rate of decomposition of AB.
Solution
AB → C + D
ravg =
Hint
Clear
Info
Incorrect Attempts:
CHECK
mol/L·s
Hint Unavailable
Average rate is like 'slope' of the change in concentration over the change in time...
ravg =
Hint
Clear
Info
Incorrect Attempts:
CHECK
mol/L·s
Hint Unavailable
Determining Order of Reactions Empirically
The table contains the experimental information for the reaction given below, at a certain temperature.
3A + B + C → 2D + E| Test | Initial [A] (mol/L) | Initial [B] (mol/L) | Initial [C] (mol/L) | Rate of Production of E (mol/(L·s)) |
| 1 | 0.4 | 0.2 | 0.3 | 0.75 × 10-2 |
| 2 | 0.8 | 0.2 | 0.3 | 3.0 × 10-2 |
| 3 | 0.4 | 0.4 | 0.3 | 1.5 × 10-2 |
| 4 | 0.4 | 0.2 | 0.6 | 3.0 × 10-2 |
Given the experimental information, calculate the rate law equation and make a general equation for the rate-determining step.
Solution
rate =
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
Here we are calculating the rate law equation experimentally... as we should.
Rate Factor:
= (Concentration Multiple)Order
Calculate the order of [A] using trials 1 & 2:
[Concentration] 0.4 → 0.8 = ×2
Rate 0.75 → 3.0 = ×4
Rate Factor:
= (Concentration Multiple)Order
4 = 2Order
Order = 2
Calculate the order of [B] using trials 1 & 3:
[Concentration] 0.2 → 0.4 = ×2
Rate 0.75 → 1.5 = ×2
Rate Factor:
= (Concentration Multiple)Order
2 = 2Order
Order = 1
Calculate the order of [C] using trials 1 & 4:
[Concentration] 0.3 → 0.6 = ×2
Rate 0.75 → 3.0 = ×4
Rate Factor:
= (Concentration Multiple)Order
4 = 2Order
Order = 2
Rate law equation: rate = k[A]2[B]1[C]2
Rate-determining step: 2A + 1B + 2C → Product(s)
rate =
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= (Concentration Multiple)Order Calculate the order of [A] using trials 1 & 2:
[Concentration] 0.4 → 0.8 = ×2
Rate 0.75 → 3.0 = ×4 Rate Factor:
= (Concentration Multiple)Order
4 = 2Order
Order = 2 Calculate the order of [B] using trials 1 & 3:
[Concentration] 0.2 → 0.4 = ×2
Rate 0.75 → 1.5 = ×2 Rate Factor:
= (Concentration Multiple)Order
2 = 2Order
Order = 1 Calculate the order of [C] using trials 1 & 4:
[Concentration] 0.3 → 0.6 = ×2
Rate 0.75 → 3.0 = ×4 Rate Factor:
= (Concentration Multiple)Order
4 = 2Order
Order = 2
Rate law equation: rate = k[A]2[B]1[C]2
Rate-determining step: 2A + 1B + 2C → Product(s)
Calculate the rate constant for this reaction.
Solution
k =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Use any one of the tests, and substitute it into the rate law equation you determined from before. I will use the data from test 1...
k =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Determine the rate of production given the initial concentrations below... Solution
| Reactant | Initial Concentration |
| [A] | 0.1 mol/L |
| [B] | 0.2 mol/L |
| [C] | 0.3 mol/L |
r =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
mol/L·s
Hint Unavailable
Since you already calculate the rate constant, just substitute the given concentrations into the rate equation.
Determining Order of Reaction Graphically
Given the graphs of (concentration over time of) production and decomposition, determine the order of reaction.
Solution

If the graph of [Concentration] Vs. Time is LINEAR, then the reaction is 0th, Zeroth order.
Solution

If the graph of the log or ln of concentration, Log[Concentration] Vs. Time or Ln[Concentration] Vs. Time is LINEAR, then the reaction is 1st, First order.


Solution

If the graph of the reciprocal of concentration, 1/[Concentration] Vs. Time is LINEAR, then the reaction is 2nd, Second order.


Given the following information, determine the overall order of the reaction. Solution
| Time (s) | [Concentration] (mol/L) |
| 10 | 1.0 |
| 20 | 0.50 |
| 30 | 0.33 |
To determine the order, sketch the three following graphs.
Look for the graph that is LINEAR. This is the order of the reaction:
0th, Zeroth order: [Concentration] Vs. Time (Regular)
1st, First order: Log[Concentration] Vs. Time (Log)... or Ln[Concentration] Vs. Time
= 2nd, Second order: 1/[Concentration] Vs. Time (Reciprocal)
↑ This is the LINEAR graph, therefore the reaction is 2nd order.
Look for the graph that is LINEAR. This is the order of the reaction:
0th, Zeroth order: [Concentration] Vs. Time (Regular)
1st, First order: Log[Concentration] Vs. Time (Log)... or Ln[Concentration] Vs. Time
= 2nd, Second order: 1/[Concentration] Vs. Time (Reciprocal)
↑ This is the LINEAR graph, therefore the reaction is 2nd order.
Which of the following is not associated with the rate of reaction?
Solution
All of the above are associated with the rate
Note that mol/L·s is the same as once rearranged.
The Varying Units of Rate Constants, k
If the units for a rate of reaction are mol/(L·s) and the units of concentration are mol/L, what would the units of k be in the following reaction?
Solution
rate = k[A]2[B]1
Try substituting to see what happens to the units
Rate Determining Step
Given the overall reaction and the mechanism steps...
Which of the following is classified as a reaction intermediate?
Solution
Reaction intermediates do not appear in the overall, net reaction. Therefore 'D' is a reaction intermediate because it gets canceled between step 2 and 3. Note that the intermediate is never included in the rate law equation.
The reaction, is an elementary reaction.
Solution
An elementary reaction goes directly from reactants to products, with no intermediate mechanism steps. However, steps 1-3 are considered elementary reaction steps...
Determine the rate law equation based on the rate-determining step.
Solution
rate =
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
Since 'D' is an intermediate it is not in the rate law equation...
Rate Law = k[B][D]
The rate determining step is based on the slow step, where the reactant coefficients of the reaction are the rate law orders. But wait there's an exception! ...
... If the slow step contains intermediates, then all the reactants in the fast step that contains the slow-step intermediate are included in the rate law...
∴ rate = k[B]2[C]1
Explanation: step 2 is 'so fast' that adding more [C] will instantly turn into [D] and is 'like adding' more [D] (even though [D] is an intermediate) which is what the slow step is 'waiting for'. Basically if [C] is doubled then [D] will quickly double. [D] produced in step 2 is limiting and dependent for step 3!
rate =
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
... If the slow step contains intermediates, then all the reactants in the fast step that contains the slow-step intermediate are included in the rate law... ∴ rate = k[B]2[C]1 Explanation: step 2 is 'so fast' that adding more [C] will instantly turn into [D] and is 'like adding' more [D] (even though [D] is an intermediate) which is what the slow step is 'waiting for'. Basically if [C] is doubled then [D] will quickly double. [D] produced in step 2 is limiting and dependent for step 3!
Integrated Rate Law, First Order
Given the integrated rate law for first order reactions, where [A]t is the concentration at time 't', k is the rate constant, and ln[A]0 is the initial concentration of the reactant.
ln[A]t = -kt + ln[A]0State what each of the quantities represents on a cartesian plane (graph). Solution Video
| Quantity | Graph Value |
| ln[A]t | |
| -k | |
| t | |
| ln[A]0 |
Based on the linear equation: y = mx + b...
| Quantity | Graph Value |
| ln[A]t | y-value (output, dependent) |
| -k | slope, m |
| t | x-value (input, independent) |
| ln[A]0 | y-intercept, b |
Why is the slope of this graph decreasing?
Solution
The slope (-k) is decreasing because the y-value, the reactant, ln[A]t is decreasing over time as it is consumed in the reaction.
The pharmacokinetics of ibuprofen shows first-order kinetics with a serum (blood) half life of approximately 2 hours. Based on a 400 mg dose, the serum concentration of ibuprofen is 30 mg/L. If the rate constant, k equals 0.3466 hr-1, determine the time for one dose to reach 1 mg/L in the blood. [This uses numbers from real lab tests]
Solution
Video
t =
Hint
Clear
Info
Incorrect Attempts:
CHECK
hours
Hint Unavailable
Given: initial concentration [A]0 = 30 mg/L, final concentration [A]t = 1 mg/L, and the rate constant k = 0.3466 hr-1...
(Notice we don't need the 2 hour half-life or the 400 mg dose.)
Rearrange the first order integrated rate law for time, then sub in...
Therefore it takes approximately 9.81 hours for the serum concentration of ibuprofen to dissipate from 30 mg/L to 1 mg/L.
t =
Hint
Clear
Info
Incorrect Attempts:
CHECK
hours
Hint Unavailable
(Notice we don't need the 2 hour half-life or the 400 mg dose.)
Rearrange the first order integrated rate law for time, then sub in... Therefore it takes approximately 9.81 hours for the serum concentration of ibuprofen to dissipate from 30 mg/L to 1 mg/L.
Integrated Rate Law, First Order Example
Determine an equation for time in a half-life equation in terms of the rate constant, k. Given that for half life, the final concentration [A]t equals half the initial concentration [A]0:
Solution
t =
Hint
Clear
Info
━━━
Incorrect Attempts:
CHECK
Hint Unavailable
Sub this into the first order integrated rate law equation for [A]t and [A]0...
t =
Hint
Clear
Info
━━━
Incorrect Attempts:
CHECK
Hint Unavailable
Integrated Rate Law, First Order Example
Half-life equations mostly follow first order kinetics. Given:
ln[A]t = -kt + ln[A]0A radioisotope decays in 145.2 days. Calculate the rate constant, k.
Solution
k =
Hint
Clear
Info
Incorrect Attempts:
CHECK
days-1
Hint Unavailable
Use the equation for time in a half-life equation, in terms of the rate constant, k
k =
Hint
Clear
Info
Incorrect Attempts:
CHECK
days-1
Hint Unavailable
If 100.0 g of this isotope decayed over 15 years, calculate the final amount remaining...
Solution
Amount =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
grams
Hint Unavailable
The equation works for concentration as well as masses...
Note that 15 years = 5475 days...
Amount =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
grams
Hint Unavailable
Note that 15 years = 5475 days...
Integrated Rate Law, Second Order
Given the integrated rate law for second order reactions, where [A]t is the concentration at time 't', k is the rate constant, and ln[A]0 is the initial concentration of the reactant.
Based on the given integrated rate law for second order reactions, what quantity is represented by the slope?
Solution
The slope is 'k'
Based on the given integrated rate law for second order reactions, what quantity is represented by the slope? What quantity is represent by the y-intercept?
Solution
The slope is 'k'
The y-intercept is
The y-intercept is
If a particular insecticide follows second order kinetics and has a rate law constant (k) of 0.555 M-1s-1, determine the initial concentration if the concentration after 10 minutes is 0.00298 M.
Solution
[A]0 =
Hint
Clear
Info
Incorrect Attempts:
CHECK
M
Hint Unavailable
Don't forget to convert 10 minutes to 600 seconds.
Therefore the initial concentration, [A]0 is 0.389 mol/L
[A]0 =
Hint
Clear
Info
Incorrect Attempts:
CHECK
M
Hint Unavailable
Flashcards: Kinetics
| What factors affect the rate of a reaction? |
| Concentration, surface area, temperature, pressure, catalysts, and solvent type. |
| Under what conditions can the reaction coefficients be used as the orders in the rate law equation? |
| Only if the coefficients are from the elementary step (no intermediates) and it is the slow, rate determining step. |
| Are reactants from fast steps sometimes included in the rate law equation? |
| Yes! If there are several mechanism steps that make up the overall reaction and the slow step contains intermediates, then the fast reaction with that intermediate has all its reactants in the rate equation. |
| Does increasing the amount of moles affect reaction rate? |
| No |
| What is a reaction intermediate? |
| Reaction intermediates do not appear in the overall, net reaction |
| Are intermediates included in the rate law equation? |
| No, never |
| What factors affect the value of the rate constant (k) in the rate equation? |
| k only depends on temperature, presence of a catalyst, or the nature of the solvent. |
| What do catalysts change in a reaction? |
| The activation energy, Ea |
| If the initial concentration of reactant A is tripled, what will happen to the rate? r = k[A]3[B]1 |
| The overall reaction rate will increase by a factor of 27 ( = [3]3 = 27) |
| What is the overall order of the reaction? r = k[A][B]2[C]2 |
| 5 |
| If the initial concentration of reactant A is doubled, what will happen to the rate? r = k[A]0[B]1[C]2 |
| Nothing happens with changes to a zero order reactant. |
| What is the rate-determining step? |
| The rate determining step in a reaction is always the slowest step in the theorized reaction mechanism. |
| Is the activation energy for the forward reaction equal in magnitude to the activation energy for the reverse of the same reaction? |
| No, the magnitudes are different, depending on the potential energies of the reactants, products, and intermediates. |
Chemical Systems and Equilibrium
Equilibrium
For the reaction equation, determine the equilibrium constant equation assuming all reactants and products are aqueous. Interpret what a low Keq value indicates.
Solution
Video
The equilibrium constant equation is:
A low Keq value indicates that at equilibrium, the concentration of the reactants [A] and [B] are greater than the concentration of the products [C] and [D]. This means that the reaction will not proceed to produce much products.
When equilibrium is reached in a chemical reaction, the forward and reverse reactions have stopped.
Solution Video
The forward and reverse reactions are always occurring, even at equilibrium - when the forward rate equals the reverse rate.
When the ion product (Q) equals Kc, or Keq, or Ksp, or Kp, the reaction is at equilibrium and can be summarized with Gibbs free energy...
Solution
∆G = 0
Gibbs free energy (when ∆G = 0) indicates the reaction is at equilibrium, similar to Q = K ...
Equilibrium Constant
A high Keq value indicates
Solution
Video
A high value indicates that at equilibrium the concentration, [] compares like this: [products] > [reactants]...
E.g.)
Equilibrium Constant Expression
Determine the correct keq equation for the following reaction.
Solution
Video
The keq equation is made of products over the reactants, and the concentration is raised to the exponent of the coefficient in front.
Equilibrium Constant Expression for Heterogeneous (2 or More Phase) Systems
Determine the correct keq equation for the following reaction.
Solution
Video
Pure solids and liquids/solvents do not appear in equilibrium constant expressions because the concentration of these things does not even make sense.
Equilibrium Constant Forward and Reverse
Determine the equilibrium constant, keq for the reverse of the following reaction.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Write the keq equations for the forward and for the reverse of the reaction and notice the reciprocal relationship.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Equilibrium and Catalysts
Catalysts shift the equilibrium position in a reaction to increase the amount of products.
Solution
Catalysts do not move the equilibrium, they only change the activation energy and the rate of reaction.
Le Châtelier’s Principle with Gases and Aqueous
Determine the effect of increasing the pressure in the system by a reasonable amount.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Since solids do not respond to typical changes in pressure (nor do liquids) because they have a constant volume, the reaction will not shift to the right, in fact it will shift to the left. Only consider the gaseous molecules that can change volume...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Which three of the following will shift the reaction to the left?
Solution
To shift the reaction to the left...
- Increase temperature, add heat
- Decrease pressure (by increasing volume)
- Remove [H2] or [O2]
- Increase [H2O]
- Increase temperature, add heat
- Decrease pressure (by increasing volume)
- Remove [H2] or [O2]
- Increase [H2O]
Determine the change that would increase the solubility of rubidium fluoride, RbF.
Solution
- Since energy is a product this is an exothermic reaction. You can drive exothermic reactions to the right, increasing solubility, by removing energy (decreasing temperature).
- Adding more reactant will not increase the solubility (molarity) of the reactant.
- Pressure does not affect solid and aqueous.
- Adding more water or shaking the solution would increase the rate of dissolving the solid, but would not increase the solubility (molarity) of the reactant, which is based on the ksp magnitude.
- Since energy is a product this is an exothermic reaction. You can drive exothermic reactions to the right, increasing solubility, by removing energy (decreasing temperature).
- Adding more reactant will not increase the solubility (molarity) of the reactant.
- Pressure does not affect solid and aqueous.
- Adding more water or shaking the solution would increase the rate of dissolving the solid, but would not increase the solubility (molarity) of the reactant, which is based on the ksp magnitude.
Different 'k' Constants
Describe some of the similarities and differences between Keq, Ksp, Kc, and Kp?
Solution
With calculations...
- They are all calculated with [products] ÷ [reactants], and raised to the power of the coefficients
- None use solids or liquids in the equations
Generally...
- Keq is the general equilibrium constant used for gases or aqueous ions...
- Kc is also the general equilibrium constant used for gases or aqueous ions...
- Ksp is used only with concentrations for solubility of aqueous ions, and uses brackets in the equation
- Kp is used only for pressure of gases, and uses parenthesis in the equation
- They are all calculated with [products] ÷ [reactants], and raised to the power of the coefficients
- None use solids or liquids in the equations
- Keq is the general equilibrium constant used for gases or aqueous ions...
- Kc is also the general equilibrium constant used for gases or aqueous ions...
- Ksp is used only with concentrations for solubility of aqueous ions, and uses brackets in the equation
- Kp is used only for pressure of gases, and uses parenthesis in the equation
Given the equation below where R is the gas constant (0.0821 L·atm/mol·K), T is temperature, and n is the amount of moles, is it possible for kp to equal kc? If not explain why, if so provide an example in support.
Solution
Yes it is possible for them to be equal. Consider the example where the moles on the left side is 2 and mols on the right side is 2...
So,
Here we can see they are the same, but often they are different.
Equilibrium Constant
Which of the following will affect the equilibrium, Ksp?
Solution
- Temperature
- Catalysts
- Concentration
Only temperature affects ksp, keq
- Temperature
- Catalysts
- Concentration
Equilibrium Calculations with ICE
Given the reaction equation below and the following initial concentrations, determine the concentration of NO(g), once equilibrium is reached after adding 0.7 mol/L of NO(g) to the system. Solution
| [ClNO2] | [NO] | [NO2] | [ClNO] |
| 0.8 mol/L | 0.1 mol/L | 0.2 mol/L | 0.3 mol/L |
[NO] =
Hint
Clear
Info
Incorrect Attempts:
CHECK
M
Hint Unavailable
The equation below can be used to determine when the 'x' value can be neglected, when it is added (or subtracted) from the initial amount.
Solution
Use this to simplify the equilibrium amount before plugging into Kc, Keq equations...
We are able to do this because a low Kc or Keq means the reaction has low amount of products at equilibrium so there is a small enough change in 'x' for the reactants or products, and can be neglected if it is added or subtracted from the initial amount... see next question for an example of this...
We are able to do this because a low Kc or Keq means the reaction has low amount of products at equilibrium so there is a small enough change in 'x' for the reactants or products, and can be neglected if it is added or subtracted from the initial amount... see next question for an example of this...
Given the reverse reaction and the following initial concentrations, determine the concentration of the products at equilibrium. Solution
| [NO2] | [ClNO] | [ClNO2] | [NO] |
| 0.1 mol/L | 0.3 mol/L | 0 mol/L | 0 mol/L |
Hint
Clear
Info
[ClNO2(g)] =
M
[NO(g)] =
M
Incorrect Attempts:
CHECK
Hint Unavailable
With a low keq (0.00083) first check if we can neglect 'x'...
When the ratio is over 100 we can neglect 'x' when it is added or subtracted.
But cannot neglect the lone 'x's...
Set up the Keq equation...
Therefore there is 0.17 M of both ClNO2 (g) and NO(g).
But cannot neglect the lone 'x's...
| [NO2] | [ClNO] | [ClNO2] | [NO] | |
| I | 0.1 mol/L | 0.3 mol/L | 0 mol/L | 0 mol/L |
| C | -x | -x | +x | +x |
| E | 0.1 - | 0.3 - | x | x |
Understanding Solubility Product Constant Ksp
Given the following reaction...
Determine the ksp formula.
Solution
Remember that solids are not used in Ksp equation because the concentration of a solid does not make sense.
What would a low Ksp value mean?
Solution
The reaction does not proceed significantly to the right, since,
A low Ksp means the [reactants] > [products]
For example, if [reactants] is over 100 times greater than [products]...
For example, if [reactants] is over 100 times greater than [products]...
You are going to calculate the ksp of a solution of calcium phosphate, Ca3(PO4)2 in your lab. Eventually you evaporate 10 L of the solution until a powder is left, which weighs 3.53 × 10 -4 grams. You got this!
Solution
ksp =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
M
Hint Unavailable
Ca3(PO4)2 is 309.9 g/mol
Moles:
The molar solubility (concentration) is
Make an ice table,
Ca3(PO4)2 (s) 3Ca2+(aq) 2PO4 (aq)3-
I -- 0 mol/L 0 mol/L
C -- + 3x + 2x
E -- 3x 2x
Calculate ksp, where x = 1.14 × 10-7 M
ksp =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
M
Hint Unavailable
Moles: The molar solubility (concentration) is Make an ice table,
| Ca3(PO4)2 (s) | 3Ca2+(aq) | 2PO4 (aq)3- | |
| I | -- | 0 mol/L | 0 mol/L |
| C | -- | + 3x | + 2x |
| E | -- | 3x | 2x |
Molar Solubility
Given the general equation below...
If the molar solubility of the compound XaYb (s) is 0.1 M, determine the solubility of the ion products in terms of a and b.
Solution
0.1 M XaYb (s) would dissociate into,
X(aq): 0.1a M
And,
Y(aq): 0.1b M
Starting from zero products, can the molar solubility of the products X(aq) and Y(aq) be different from molar solubility of XaYb (s) times the coefficient 'a' or 'b'?
Solution
No, the molar solubility would always be 0.1a M of X(aq) and 0.1b M of Y(aq) because the reaction equation would always have a coefficient of one, so like 1XaYb (s)...
Solubility Product Constant Ksp Calculation
Given the following equation, determine the solubility of calcium hydroxide in water by determining the concentration of the calcium ion at equilibrium.
Solution
[Ca(OH)2] =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
M
Hint Unavailable
Set up the ICE table for Ksp just like you are used to for keq...
Ca(OH)2 Ca2+ 2OH-
initial n/a 0 0
change n/a +x +2x
equilibrium n/a x 2x
Remember Ksp does not include solids because the concentration of a solid does not make sense.
[Ca(OH)2] =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
M
Hint Unavailable
| Ca(OH)2 | Ca2+ | 2OH- | |
| initial | n/a | 0 | 0 |
| change | n/a | +x | +2x |
| equilibrium | n/a | x | 2x |
Temperature and Ksp
Nitrate salts are typically highly soluble and can be assumed to dissociate completely. Solid silver nitrate, AgNO3 is dissolved until saturation in water at 1 atm at the three different temperatures in the test tubes below.
| Tube A, 20˚C | Tube B, 60˚C | Tube C, 100˚C |
| 12.7 M | 25.9 M | 43.1 M |
Calculate the Ksp at each temperature.
Solution
Hint
Clear
Info
Tube A, 20˚C Tube B, 60˚C Tube C, 100˚C
12.7 M 25.9 M 43.1 M
Ksp = Ksp = Ksp =
Incorrect Attempts:
CHECK
Hint Unavailable
(Only temperature can affect Ksp...)
At 20˚C...
At 60˚C...
At 100˚C...
Hint
Clear
Info
| Tube A, 20˚C | Tube B, 60˚C | Tube C, 100˚C |
| 12.7 M | 25.9 M | 43.1 M |
| Ksp = | Ksp = | Ksp = |
Incorrect Attempts:
CHECK
Hint Unavailable
At 20˚C... At 60˚C... At 100˚C...
Calculate the percent increase in Ksp from 20˚C → 100˚C.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
%
Hint Unavailable
Percent increase is,
Hint
Clear
Info
Incorrect Attempts:
CHECK
%
Hint Unavailable
Determine Ksp Given Equilibrium Concentration
It is possible to calculate the solubility product constant, Ksp given only the solubility of a salt at a certain temperature.
Solution
For example with copper(II) fluoride, the equation is
If the solubility at a certain temperature is 0.05M, then this is the concentration at equilibrium of the copper ions and 2 times the fluoride ions.
Create an ICE table and the Ksp formula to calculate...
Create an ICE table and the Ksp formula to calculate...
Determine the Ksp of CuF2 if the equilibrium concentration (at a certain extreme temperature) of F-(aq) is 0.002 mol/L and the reaction starts with 100% reactants.
Solution
Ksp =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
M
Hint Unavailable
CuF2 Cu2+ 2F-
initial n/a 0 0
change n/a +x +2x
equilibrium n/a x 2x
At equilibrium, the [F-] = 2x = 0.002 mol/L
x = 0.001 mol/L
Solids are not included in Ksp equations...
Ksp = [Cu2+]1[F-]2
= [x]1[2(x)]2
= [0.001]1[2(0.001)]2
= 4.0 × 10-9 mol/L
Ksp =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
M
Hint Unavailable
| CuF2 | Cu2+ | 2F- | |
| initial | n/a | 0 | 0 |
| change | n/a | +x | +2x |
| equilibrium | n/a | x | 2x |
x = 0.001 mol/L
Solids are not included in Ksp equations... Ksp = [Cu2+]1[F-]2
= [x]1[2(x)]2
= [0.001]1[2(0.001)]2
= 4.0 × 10-9 mol/L
Determine Ion Concentration at Equilibrium Given Ksp
Given the Ksp below, the molar solubility of CaF2 (s) is 0.40 M, so [F-] = 0.40 M, and [Ca2+] = 9.25 × 10-8 M.
Solution
CaF2 Ca2+ 2F-
initial n/a 0 0
change n/a +x +2x
equilibrium n/a x 2x
Do not include solids in k constant equation...
CaF2 Ca2+ 2F-
initial n/a 0 0
change n/a +x +2x
equilibrium n/a 0.0021 M 2(0.0021 M) = 0.0042 M
False, [F-] does not equal 0.40 M, and [Ca2+] does not equal 9.25 × 10-8 M.
| CaF2 | Ca2+ | 2F- | |
| initial | n/a | 0 | 0 |
| change | n/a | +x | +2x |
| equilibrium | n/a | x | 2x |
| CaF2 | Ca2+ | 2F- | |
| initial | n/a | 0 | 0 |
| change | n/a | +x | +2x |
| equilibrium | n/a | 0.0021 M | 2(0.0021 M) = 0.0042 M |
Given the solubility product constant (Ksp) of calcium phosphate, Ca3(PO4)2 is 2.1 × 10-33, determine the concentration of phosphate, PO4 in the calcium fluoride solution at equilibrium.
Solution
[PO4] =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
M
Hint Unavailable
You already calculated the concentration of calcium is 0.0021 M at equilibrium. Use this as the initial amount for the dissociation of calcium phosphate.
Ca3(PO4)2 3Ca2+ 2PO43-
initial n/a 0.0021 M 0 M
change n/a + 3x + 2x
equilibrium n/a 0.0021 M + 3x 2x
Hopefully this made sense to you, you used the solubility product constant of calcium phosphate and neglected the change in x for the calcium.
[PO4] =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
M
Hint Unavailable
| Ca3(PO4)2 | 3Ca2+ | 2PO43- | |
| initial | n/a | 0.0021 M | 0 M |
| change | n/a | + 3x | + 2x |
| equilibrium | n/a | 0.0021 M | 2x |
Gases (With and Without Partial Pressures)
The breakdown of ammonia is the reverse of the Haber process. Calculate the reaction quotient, q for the breakdown of ammonia under certain conditions...
Starting with 1.2 mol ammonia, 3.2 mol nitrogen, and 4.5 mol hydrogen, in a 2L container at a certain temperature.
Solution
q =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Don't need to calculate the partial pressures here... the reaction quotient, q just uses the molarity of the gas (mol/L)...
Calculate reaction quotient, q...
(Then you would compare this value with k to see where the reaction is compared to equilibrium, hence if shifts to left or right...)
q =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
If the total pressure is 7.5 atm at a different temperature, use mole fractions to calculate partial pressure to calculate the new reaction quotient.
Solution
qp =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(The partial pressure is the pressure that a gas in the mixture would exert if it was the only gas in the container.)
First calculate the mole fraction of each of the gases...
Then calculate the partial pressures..
Just plug the 'partial pressures' of the gases right into the reaction quotient equation, q. Make sure to include "P" for partial pressure in your equation...
(Then you would compare this value with k to see where the reaction is compared to equilibrium, hence if shifts to left or right...)
qp =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
First calculate the mole fraction of each of the gases... Then calculate the partial pressures.. Just plug the 'partial pressures' of the gases right into the reaction quotient equation, q. Make sure to include "P" for partial pressure in your equation... (Then you would compare this value with k to see where the reaction is compared to equilibrium, hence if shifts to left or right...)
If the equilibrium constant (Kp) is 9,000 then calculate the partial pressures at equilibrium starting with 1 atm of ammonia.
Solution
P:
Hint
Clear
Info
NH3 = N2 = H2 =
Incorrect Attempts:
CHECK
atm
Hint Unavailable
Since Q << K, then the reaction will shift to the right...
Use an ice table,
2NH3 (g) ↔ N2 (g) 3H2 (g)
I (Initial) 1 atm 0 0
C (Change) - 2x + x + 3x
E (Equilibrium) 1 - 2x x 3x
Calculate the change given the equilibrium constant (Kp) is 9,000
Since the ratio of the lowest partial pressure to 'k' is less than 100, we cannot neglect where 'x'...
Since we start with 1 atm, we can neglect the outliers -37 and 36...
Average and round the middle values... x = 0.5
Therefore at equilibrium there is:
- ammonia: 1 - 2(0.5) = 0 atm
- nitrogen: 0.5 atm
- hydrogen: 3(0.5) = 1.5 atm
P:
Hint
Clear
Info
NH3 = N2 = H2 =
Incorrect Attempts:
CHECK
atm
Hint Unavailable
Use an ice table,
| 2NH3 (g) ↔ | N2 (g) | 3H2 (g) | |
| I (Initial) | 1 atm | 0 | 0 |
| C (Change) | - 2x | + x | + 3x |
| E (Equilibrium) | 1 - 2x | x | 3x |
Since the ratio of the lowest partial pressure to 'k' is less than 100, we cannot neglect where 'x'... Since we start with 1 atm, we can neglect the outliers -37 and 36...
Average and round the middle values... x = 0.5
Therefore at equilibrium there is:
- ammonia: 1 - 2(0.5) = 0 atm
- nitrogen: 0.5 atm
- hydrogen: 3(0.5) = 1.5 atm
Solubility Product Constant Ksp and Ion Product Constant Qsp
If the solution is not at equilibrium, then Qsp is used instead of Ksp.
Solution
True


If Ksp = Qsp then
Solution
The reaction is at equilibrium between the reactants and products.
No precipitate will form.
No precipitate will form.
When Ksp > Qsp, some more of the compound would be able to dissociate into solution.
Solution
Video
Ksp is a constant, while Qsp is a 'gauge' of the ion concentrations before equilibrium is reached. So if Qsp is higher than Ksp, too many ions are present and some precipitate will form. Conversely, if Qsp is lower than Ksp, this means there is still room for ions to dissolve and more of the compound will dissociate.
Precipitate Formation
The most abundant ions in hard tap water are calcium, Ca2+ and magnesium, Mg2+. Given the Ksp values of various compounds, determine which would make the best water softener, in other words, which would precipitate the calcium and magnesium ions. Solution
| Ksp | Ca2+ | Mg2+ |
| CO32- | 4 × 10-9 | 6.8 × 10-6 |
| F- | 3.5 × 10-11 | 5.2 × 10-11 |
| PO43- | 2.1 × 10-33 | 1 × 10-24 |
| OH- | 5 × 10-6 | 5.6 × 10-12 |
| ClO3- | > 100 | > 100 |
Water softeners replace the calcium and magnesium ions with much more soluble lithium Li+, sodium Na+, and potassium K+ ions.
The lowest Ksp precipitates the calcium and magnesium out of solution - and is the best water softener. So the phosphate salt is the best water softener. K3PO4
The lowest Ksp precipitates the calcium and magnesium out of solution - and is the best water softener. So the phosphate salt is the best water softener. K3PO4
Precipitate Formation
Mixing 0.15 L of a 0.02 M solution of lithium carbonate with 0.02L of 0.1 M solution of zinc fluoride...
Determine the concentration of zinc ions and carbonate ions in the mixed solution.
Solution
Hint
Clear
Info
[Zn+] = [CO32-] =
Incorrect Attempts:
CHECK
M
Hint Unavailable
Be careful - when the solutions are mixed the volume increases and the concentration of the ions decreases.
Concentration of zinc ions,
Concentration of carbonate ions,
Hint
Clear
Info
[Zn+] = [CO32-] =
Incorrect Attempts:
CHECK
M
Hint Unavailable
Concentration of zinc ions, Concentration of carbonate ions,
Given the solubility product constant of zinc carbonate, ZnCO3(s) is 1.19 × 10-10, determine whether a precipitate of zinc carbonate will form in the mixture.
Solution
Hint
Clear
Info
Qsp =× 10
Will a precipitate form?
Incorrect Attempts:
CHECK
Hint Unavailable
A precipitate forms when Qsp > Ksp
ZnCO3 (s) ↔ Zn2+(aq) CO32-(aq)
I (Initial) -- 0 M 0 M
C (Change) -- + x + x
E (Equilibrium) -- x x
Calculate Q...
Since Qsp > Ksp, then yes a precipitate will form.
Hint
Clear
Info
Qsp =× 10
Will a precipitate form?
Will a precipitate form?
Incorrect Attempts:
CHECK
Hint Unavailable
| ZnCO3 (s) ↔ | Zn2+(aq) | CO32-(aq) | |
| I (Initial) | -- | 0 M | 0 M |
| C (Change) | -- | + x | + x |
| E (Equilibrium) | -- | x | x |
All About Precipitates
A solution contains an initial 0.001 M concentration of fluoride and sulfate ions. Good luck!
When strontium chlorate, Sr(ClO3)2 - which is considered very soluble - is added to the solution, determine the salt that will precipitate first. Show your work.
Solution
Adding the strontium chlorate, Sr(ClO3)2 is basically like adding [Sr2+] ...
You can calculate the concentration [Sr2+] at equilibrium using the ksp. The precipitate forms when the ion product (Q) is ≥ Ksp. You know the lower (concentration of) [Sr2+] at equilibrium will precipitate first.
SrF2(s) Sr2+(aq) 2 F-(aq)
I (Initial) -- 0 M 0.001 M
C (Change) -- + x + 2x
E (Equilibrium) -- x 0.001 + 2x
SrSO4(s) Sr2+(aq) SO42-(aq)
I (Initial) -- 0 M 0.001 M
C (Change) -- + x + x
E (Equilibrium) -- x 0.001 + x
Since the ratio of initial concentration 0.001M to the ksp is greater than 100, you can neglect wherever 'x' is added...
At equilibrium, since the (concentration of) [Sr2+] from SrSO4 is lower than the (concentration of) [Sr2+] from SrF2, the SrF2 will start to precipitate first.
You can calculate the concentration [Sr2+] at equilibrium using the ksp. The precipitate forms when the ion product (Q) is ≥ Ksp. You know the lower (concentration of) [Sr2+] at equilibrium will precipitate first.
| SrF2(s) | Sr2+(aq) | 2 F-(aq) | |
| I (Initial) | -- | 0 M | 0.001 M |
| C (Change) | -- | + x | + 2x |
| E (Equilibrium) | -- | x | 0.001 |
| SrSO4(s) | Sr2+(aq) | SO42-(aq) | |
| I (Initial) | -- | 0 M | 0.001 M |
| C (Change) | -- | + x | + x |
| E (Equilibrium) | -- | x | 0.001 |
Since the ratio of initial concentration 0.001M to the ksp is greater than 100, you can neglect wherever 'x' is added...
At equilibrium, since the (concentration of) [Sr2+] from SrSO4 is lower than the (concentration of) [Sr2+] from SrF2, the SrF2 will start to precipitate first.
Calculate the molarity of strontium chlorate, Sr(ClO3)2 when the first precipitate starts to precipitate.
Solution
[Sr(ClO3)2] =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
mol/L
Hint Unavailable
Since you already solved the concentration of strontium ions when the first precipitate forms...
And the molar ratio of strontium ions to strontium chlorate is 1 Sr2+ : 1 Sr(ClO3)2, then the molarity of strontium chlorate is the same...
(Aside: the molarity of the chlorate ions would be twice this, 2 × 3.4 × 10-4 = 6.8 × 10-4).
[Sr(ClO3)2] =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
mol/L
Hint Unavailable
Now that you know the order of precipitation, calculate the concentration of sulfate, SO42- ions when strontium fluoride, SrF2 begins to precipitate.
Solution
[SO42-] =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
mol/L
Hint Unavailable
You already know the SrSO4 precipitates first → then the SrF2 begins to precipitate...
You already calculated when the strontium fluoride, SrF2 begins to precipitate, the concentration of [Sr2+] ions at this point is
[Sr2+] = 4.3 × 10-3 M
Now use this ↑ concentration of [Sr2+] ions in the ksp equation for strontium sulfate, SrSO4...
[SO42-] =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
mol/L
Hint Unavailable
You already calculated when the strontium fluoride, SrF2 begins to precipitate, the concentration of [Sr2+] ions at this point is [Sr2+] = 4.3 × 10-3 M Now use this ↑ concentration of [Sr2+] ions in the ksp equation for strontium sulfate, SrSO4...
The Common Ion
If 80mL of 0.6M MgBr2 is mixed with 100mL of 0.7M LiBr, find the total concentration of the bromide (Br-) ions, both salts are considered very soluble.
Solution
[Br-] =
Hint
Clear
Info
Incorrect Attempts:
CHECK
mol/L
Hint Unavailable
[Br-] =
Hint
Clear
Info
Incorrect Attempts:
CHECK
mol/L
Hint Unavailable
The Common Ion Effect
Adding some solid Pb(NO3)2 to a saturated solution of PbCrO4 at equilibrium will precipitate some PbCrO4 and the [CrO42-] will decrease.
Solution
Lead (Pb2+) is the common ion...
Nitrate is very soluble and so many more lead (Pb2+) ions will dissolve into solution, causing the reaction to shift to the left because of Le Chatelier's principle. Basically, since temperature (and hence Ksp) is constant, increasing the concentration of lead ions will decrease the [CrO42-] (concentration of chromate ions) causing some PbCrO4 to precipitate.
Lead chromate, PbCrO4 would be most soluble in a solution containing...
Solution
Any solutions already containing either lead, Pb2+ or chromate, CrO42- ions would make the lead chromate, PbCrO4 less soluble.
Lead nitrate, Pb(NO3)2 would be least soluble in a solution containing...
Solution
Common ion will reduce the solubility of lead nitrate, Pb(NO3)2.
The sodium nitrate is extremely soluble and will dissociate many nitrate, NO3- ions into solution. Even more than the 2 mols from barium nitrate...
The Common Ion Effect
The solubility product constant (Ksp) of calcium sulfate and silver sulfate are given at 25˚C.
Calculate the solubility of Ag2SO4 in pure water.
Solution
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
M
Hint Unavailable
Make an ICE table,
Ag2SO4 (s) ↔ 2Ag+(aq) SO42-(aq)
I (Initial) -- 0 M 0 M
C (Change) -- + 2x + x
E (Equilibrium) -- 2x x
Sub the molar solubility at equilibrium, 'x' into the solubility product constant equation...
This is the (molar) solubility of Ag2SO4 in pure water.
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
M
Hint Unavailable
| Ag2SO4 (s) ↔ | 2Ag+(aq) | SO42-(aq) | |
| I (Initial) | -- | 0 M | 0 M |
| C (Change) | -- | + 2x | + x |
| E (Equilibrium) | -- | 2x | x |
Calculate the solubility of CaSO4 in a saturated solution of Ag2SO4 (s) (assuming excess silver sulfate).
Solution
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
M
Hint Unavailable
Make an ICE table, starting with 1.4 × 10-2 M SO42- because it is a saturated solution...
CaSO4 (s) ↔ Ca2+(aq) SO42-(aq)
I (Initial) -- 0 M 1.4 × 10-2 M
C (Change) -- + x 1.4 × 10-2 M + x
E (Equilibrium) -- x 1.4 × 10-2 + x
IMPORTANT! - first see if you can neglect 'x', if the ratio of the molar solubility to the Ksp is greater than 100...
Since the ratio is > 100, then you can neglect 'x' because it is considered a small or negligible change compared to the molar solubility 1.4 × 10-2...
CaSO4 (s) ↔ Ca2+(aq) SO42-(aq)
I (Initial) -- 0 M 1.4 × 10-2 M
C (Change) -- + x 1.4 × 10-2 M + x
E (Equilibrium) -- x 1.4 × 10-2
Sub the molar solubility at equilibrium, 'x' into the solubility product constant equation...
This is the (molar) solubility...
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
M
Hint Unavailable
| CaSO4 (s) ↔ | Ca2+(aq) | SO42-(aq) | |
| I (Initial) | -- | 0 M | 1.4 × 10-2 M |
| C (Change) | -- | + x | 1.4 × 10-2 M + x |
| E (Equilibrium) | -- | x | 1.4 × 10-2 + x |
| CaSO4 (s) ↔ | Ca2+(aq) | SO42-(aq) | |
| I (Initial) | -- | 0 M | 1.4 × 10-2 M |
| C (Change) | -- | + x | 1.4 × 10-2 M |
| E (Equilibrium) | -- | x | 1.4 × 10-2 |
The Common Ion Effect
The solubility product constant of barium nitrate Ba(NO3)2 at 25˚C is,
Calculate the molar solubility of barium nitrate in pure water.
Solution
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
M
Hint Unavailable
ICE table,
Ba(NO3)2 (s) ↔ Ba2+(aq) 2NO3-(aq)
I (Initial) -- 0 M 0 M
C (Change) -- + x + 2x
E (Equilibrium) -- x 2x
Sub into Ksp to find molar solubility of barium nitrate...
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
M
Hint Unavailable
| Ba(NO3)2 (s) ↔ | Ba2+(aq) | 2NO3-(aq) | |
| I (Initial) | -- | 0 M | 0 M |
| C (Change) | -- | + x | + 2x |
| E (Equilibrium) | -- | x | 2x |
Given the molar solubility of barium iodate, Ba(IO3)2 in pure 25˚C water is 1 × 10-3 M, calculate the solubility product constant (Ksp) of barium iodate.
Solution
Ksp =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
Hint Unavailable
ICE-ice baby,
Ba(IO3)2 (s) ↔ Ba2+(aq) 2IO3-(aq)
I (Initial) -- 0 M 0 M
C (Change) -- + x + 2x
E (Equilibrium) -- x 2x
Calculate,
Ksp =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
Hint Unavailable
| Ba(IO3)2 (s) ↔ | Ba2+(aq) | 2IO3-(aq) | |
| I (Initial) | -- | 0 M | 0 M |
| C (Change) | -- | + x | + 2x |
| E (Equilibrium) | -- | x | 2x |
Calculate the molar solubility of barium iodate in a saturated solution of barium nitrate.
Solution
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
M
Hint Unavailable
Starting with some initial concentration of barium, Ba2+(aq) this time because it is a saturated solution of barium nitrate... The amount of iodate still starts at zero because the barium iodate starts as all solid first...
Ba(IO3)2 (s) ↔ Ba2+(aq) 2IO3-(aq)
I (Initial) -- 1 × 10-1 M 0 M
C (Change) -- 1 × 10-1+ x + 2x
E (Equilibrium) -- 1 × 10-1 + x 2x
Can we neglect 'x'?
Since > 100, then yes we can neglect 'x' where it is added or subtracted in the ICE table...
Ba(IO3)2 (s) ↔ Ba2+(aq) 2IO3-(aq)
I (Initial) -- 1 × 10-1 M 0 M
C (Change) -- 1 × 10-1 + x + 2x
E (Equilibrium) -- 1 × 10-1 2x
Calculate,
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
M
Hint Unavailable
| Ba(IO3)2 (s) ↔ | Ba2+(aq) | 2IO3-(aq) | |
| I (Initial) | -- | 1 × 10-1 M | 0 M |
| C (Change) | -- | 1 × 10-1+ x | + 2x |
| E (Equilibrium) | -- | 1 × 10-1 + x | 2x |
| Ba(IO3)2 (s) ↔ | Ba2+(aq) | 2IO3-(aq) | |
| I (Initial) | -- | 1 × 10-1 M | 0 M |
| C (Change) | -- | 1 × 10-1 | + 2x |
| E (Equilibrium) | -- | 1 × 10-1 | 2x |
Solubility and Precipitates
When a solution of calcium ions is dripped into a solution containing CaO and CaI2 compounds, the precipitate formed first will be the one with the solubility product (Ksp) exceeded first (lowest).
Volatile Products and Equilibrium
In an open beaker, adding more Ca2+ to the solution will significantly increase the amount of calcium carbonate precipitate.
Solution
The volatile carbon dioxide gas bubbles out of the solution and will not be present for additional calcium ions to synthesize more calcium carbonate with. The formation of the volatile carbon dioxide gas creates a one-way reaction, as can be seen from the direction of the arrow in the equation. (There will be an insignificant increase in the amount of calcium carbonate precipitate, Le Chatelier's principle)
Flashcards: Chemical Systems & Equilibrium
| At equilibrium are the forward and reverse reactions stopped? |
| No, the forward and reverse reactions are always occurring, even at equilibrium. At equilibrium the rate of the forward and reverse reactions are equal so there appears to be a balance. |
| State at least three ways to shift the equilibrium of this reaction to the left |
| Decrease pressure, increase volume, increase temperature, increase [H2O], decrease [H2] or [O2]. |
| What does a low Keq value indicate? |
| [products] > [reactants] |
| Determine the correct Keq equation for: |
| What phases do not appear in the equilibrium constant (Keq) equation? |
| Pure solids and liquids do not appear. (aqueous and gaseous do appear) |
| If the equilibrium constant for the forward reaction is Keq = 8, then what is the equilibrium constant for the reverse reaction? |
| ⅛ |
| What does a Keq much greater than and much less than 1 mean? |
| A Keq much greater than 1 means the concentration of the product is higher than the concentration of the reactant. A Keq much less than 1 means the concentration of the product is lower than the concentration of the reactant. |
Acid-Base Equilibrium
Svante Arrhenius 1884
Arrhenius defined acids and bases as
Solution
According to Arrhenius,
Acids are proton (H+) donors, and bases are hydroxide (OH-) donors
(Arrhenius' definitions become outdated when Brønsted and Lowry offered their definitions, and later Lewis...)
Acids are proton (H+) donors, and bases are hydroxide (OH-) donors
(Arrhenius' definitions become outdated when Brønsted and Lowry offered their definitions, and later Lewis...)
Johannes Brønsted and Thomas Lowry 1923
Brønsted and Lowry defined acids and bases as
Solution
According to Brønsted and Lowry,
Acids are proton (H+) donors, and bases are proton (H+) acceptors
(Brønsted and Lowry's definition was more general than Arrhenius' and encompassed more circumstances)
Acids are proton (H+) donors, and bases are proton (H+) acceptors
(Brønsted and Lowry's definition was more general than Arrhenius' and encompassed more circumstances)
Arrhenius, Brønsted-Lowry
Ammonia (NH3) violates which definition of a base?
Solution
Ammonia does not contain hydroxide (OH-) ions.
For example in pure water, Ammonia, NH3 is a Brønsted-Lowry base because it is a proton acceptor, but is not a hydroxide donor according to Arrhenius' definition. (Arrhenius defined bases as hydroxide donors).
As you can see the base, ammonia is a proton acceptor (Brønsted-Lowry base) but does not fall under the Arrhenius category of a base (hydroxide donor).
For example in pure water, Ammonia, NH3 is a Brønsted-Lowry base because it is a proton acceptor, but is not a hydroxide donor according to Arrhenius' definition. (Arrhenius defined bases as hydroxide donors). As you can see the base, ammonia is a proton acceptor (Brønsted-Lowry base) but does not fall under the Arrhenius category of a base (hydroxide donor).
pH + pOH = 14
If the pOH of a solution is 8.4, then the pH is 1.6
Solution
pH + pOH = 14
pH = 14 - 8.4
pH = 5.6
pH = 14 - 8.4
pH = 5.6
Calculate pH, pOH, [H3O+], and [OH-] - without Kw
Calculate the pH of a solution with [H+(aq)] = 2.8 × 10-3 mol/L.
Solution
Note that H+ = H3O+
Determine the pH of a solution with [OH-] = 1.0 × 10-6 mol/L
Solution
pH =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Calculate pOH...
Subtract from 14 using the equation...
(Method II is to convert [OH-] to [H3O+] = 1.0 × 10-8 mol/L ... and then calculate the pH...)
pH =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Is it possible to have a negative pH? Explain.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Yes/no, plus explain
Yes it is possible for very strong acids when the concentration of proton or hydronium ions is greater than 1.0 for example,
As you can see all it takes is for an acid with a high dissociation constant and a high molarity of the acidic protons. In this case the pOH would be 14.08
Hint
Clear
Info
Incorrect Attempts:
CHECK
Yes/no, plus explain
Polyprotic and Molar Equivalent (Normality)
A 1.0 mol/L solution of H2SO4 would have what effective equivalent of protons?
Solution
[H+] =
Hint
Clear
Info
Incorrect Attempts:
CHECK
mol/L
Hint Unavailable
There are 2 protons in each molecule of H2SO4. Since this is a strong acid it dissociates almost completely.
This makes: 2(1.0 mol/L)
= 2.0 mol/L
[H+] =
Hint
Clear
Info
Incorrect Attempts:
CHECK
mol/L
Hint Unavailable
This makes: 2(1.0 mol/L)
= 2.0 mol/L
pH with Bases
Calculate the pH of a solution prepared by completely dissolving 0.85 g of the strong base, Ca(OH)2 into 3.0 L of water.
Solution
pH =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Be careful because calcium hydroxide is di-hydroxic - there are two hydroxides...
DON'T NEED TO USE ICE TABLES FOR THE STRONG ACIDS/BASES (ONLY USE ICE TABLES FOR THE WEAKER ONES THAT DONT FULLY DISSOCIATE)...
Calculate concentration... without kb or ICE table because you assume the strong bases dissociates fully...
Since there it is di-hydroxic...
Calculate pOH
Use the formula: pH + pOH = 14
pH =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
DON'T NEED TO USE ICE TABLES FOR THE STRONG ACIDS/BASES (ONLY USE ICE TABLES FOR THE WEAKER ONES THAT DONT FULLY DISSOCIATE)... Calculate concentration... without kb or ICE table because you assume the strong bases dissociates fully... Since there it is di-hydroxic... Calculate pOH Use the formula: pH + pOH = 14
Amphoteric
Which of the following compounds is not amphoteric?
Solution
Amphoteric means that the molecule can act as either an acid or a base depending on what else is there with it in the surroundings. Of all the molecules: H2SO4 is the only molecule that is acidic and can't act as a base.
Amphoteric compounds are not located on the far left or far right ends of the equations shown above.
Write the two separate reactions of water acting as an amphoteric acid and base. One reaction with the acid, H2SO4 and the other reaction with the base, NaOH.
Solution
With H2SO4,
H2O + H2SO4 ↔ H3O+ + HSO4-
With NaOH,
H2O + NaOH ↔ Na+OH- + H2O
Conjugates of Acids and Bases
Strong acids have strong conjugate bases.
Solution
The stronger the acid, the weaker is its conjugate base.
The conjugate base of water in the following reaction is
Solution
Water is acidic when it is with a compound that acts as a base. Water is amphoteric (acts as either acid or base) depending on the other reactant it is with. Here the water is weakly acidic and forms a strong conjugate base, OH-.
Based on your knowledge of conjugate acid-base strengths, which of the following is the strongest base?
Solution
The following are all conjugate bases of strong acids, therefore they are weak bases: NaCl, NaNO3, Na2SO4, NaBr.
Weak acids have strong conjugate bases. The weak acetic acid (CH3COOH or C2H4O2) will have a strong conjugate base... C2H3O2-
CH3COOH + H2O ↔ CH3COO- + H3O+
Therefore the acetate salt (NaCH3COO or NaC2H3O2) is the strongest base...
Weak acids have strong conjugate bases. The weak acetic acid (CH3COOH or C2H4O2) will have a strong conjugate base... C2H3O2- CH3COOH + H2O ↔ CH3COO- + H3O+ Therefore the acetate salt (NaCH3COO or NaC2H3O2) is the strongest base...
Mixing Strong/Weak Acids/Bases
Mixing equal moles of weak acid and strong base results in...
Solution
Mixing equal moles is what matters most, and is needed for comparison. Mixing equal moles of weak acid and strong base always results in an alkaline/basic salt solution.
Mixing equal molarity (concentrations) of strong acids and weak bases, from two different containers, always results in an acidic solution.
Solution
Not necessarily, while this is often true, there are some situations where it is not true. For instance, if the volume of the container of the base is far greater, then the total moles of base (OH-) is greater than the total moles of acid (H3O+), and the solution would be basic.
With acid and base mixtures, it is the total amount of moles of the acid and the base that is compared.
With acid and base mixtures, it is the total amount of moles of the acid and the base that is compared.
Fill in the blanks in the table with the different mixtures of strong or weak acids and bases... Solution
| Reaction | Result |
| Neutral | |
| __________ | |
| __________ | |
| __________ | |
| __________ |
This year, you are expected to know the 6 common strong acids and 7 common strong bases, and apply this knowledge. You also need to know,
Strong Acid + Strong Base ↔ Neutral Salt + Water
Weak Acid + Strong Base ↔ Basic/Alkaline Salt + Water
Strong Acid + Weak Base ↔ Acidic Salt + Water
Weak Acid + Strong Base ↔ Basic/Alkaline Salt + Water
Strong Acid + Weak Base ↔ Acidic Salt + Water
| Reaction | Result |
| Neutral, both are strong | |
| Basic/Alkaline, KOH is strong base, acetic acid is weak acid | |
| Acidic, nitric acid is strong, and ammonia is weak base | |
| Basic, H3PO4 is a weak acid and Ca(OH)2 is strong base | |
| Neutral, both are strong |
Calcium oxalate, Ca(C2O4)2 is the most common type of kidney stone, at around 80% of kidney stone occurrences. Classify this salt...
Solution
Write the reaction with the simple Arrhenius base (-OH) and acid (-H) that makes the calcium oxalate salt. You should be able to determine this reaction on your own,
Ca(OH)2 is one of the 7 most common strong bases and HC2O4 is a weak acid (because it is not on the list of the 6 common strong acids that you should know).
The salt of a strong base, Ca(OH)2 and weak acid, HC2O4 is an alkaline salt.
The salt of a strong base, Ca(OH)2 and weak acid, HC2O4 is an alkaline salt.
Determine the result of the solution when you mix the weak mono-protic acid and weak mono-hydroxic base, with the dissociation constants, k given below. [1]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The strength of an acid or base depends on its amount of dissociation - strong will dissociate almost completely into aqueous ions.
This weak acid will dissociate (dissolve) more than the weak base because the acid has the higher dissociation constant, k. Since each is mono-protic and mono-hydroxic (1 H and 1 OH), therefore the resulting solution will be slightly more acidic.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
This weak acid will dissociate (dissolve) more than the weak base because the acid has the higher dissociation constant, k. Since each is mono-protic and mono-hydroxic (1 H and 1 OH), therefore the resulting solution will be slightly more acidic.
Precipitation of Strong and Weak Acids
A solution contains equal concentrations of the ions dissociated from a weak acid and a strong acid. Theoretically, if a common ion of the acid and base is added to the solution, the stronger acid will precipitate first.
Solution
Strong acids dissolve to almost to completion compared to weak acids. The ions of strong acids are more stable when dissolved in solution and tend to stay dissolved, whereas weaker acids precipitate more.
The Ionization Constant of Water (Kw): Calculate pH, pOH, [H3O+], and [OH-]
Given [H3O+] = 10-4, the [OH-] equals
Solution
Know the two formulas...
See for yourself, in this table, as pH increases, pOH decreases by the same amount.
pH
[H3O+]
[OH-]
pOH
1
10-1
10-13
13
2
10-2
10-12
12
3
10-3
10-11
11
4
10-4
10-10
10
5
10-5
10-9
9
6
10-6
10-8
8
7
10-7
10-7
7
8
10-8
10-6
6
9
10-9
10-5
5
10
10-10
10-4
4
11
10-11
10-3
3
12
10-12
10-2
2
13
10-13
10-1
1
| pH | [H3O+] | [OH-] | pOH |
| 1 | 10-1 | 10-13 | 13 |
| 2 | 10-2 | 10-12 | 12 |
| 3 | 10-3 | 10-11 | 11 |
| 4 | 10-4 | 10-10 | 10 |
| 5 | 10-5 | 10-9 | 9 |
| 6 | 10-6 | 10-8 | 8 |
| 7 | 10-7 | 10-7 | 7 |
| 8 | 10-8 | 10-6 | 6 |
| 9 | 10-9 | 10-5 | 5 |
| 10 | 10-10 | 10-4 | 4 |
| 11 | 10-11 | 10-3 | 3 |
| 12 | 10-12 | 10-2 | 2 |
| 13 | 10-13 | 10-1 | 1 |
The Ionization Constant of Water (Kw)
Derive the ionization constant of water, Kw using the weak acid, HF and your knowledge of Ka and Kb.
Solution
For the acid,
For the base,
Since Kw = Ka × Kb...
At SATP 25˚C, Kw = 1.0 × 10-14
Ka given Kb
Determine Ka given Kb = 5.0 × 10-3 at SATP.
Solution
Ka =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
Hint Unavailable
Ka × Kb = Kw = 1.0 × 10-14
Ka =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
Hint Unavailable
Describe what a high ka means. [1]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Since ka is the ratio of the concentration of products to the reactants,
Then a high ka value means the reaction proceeds significantly to the right - to the products. This is a strong acid. Strength of an acid depends on the amount of dissociation into ions in solution.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Acid Ionization Ka
A 0.9M solution of hydrofluoric acid dissociates into 0.0237M [F-]. Calculate the Ka of the compound.
Solution
Ka =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
Hint Unavailable
Set up an ICE table to determine the ka...
HF --> H+ + F-
Ka =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
Hint Unavailable
HF --> H+ + F-
Base Ionization Kb
Ammonia is a common household cleaner that is highly soluble in water. A solution of ammonia forms ammonium and hydroxide in solution according to the following equation.
Determine an equation for the equilibrium ionization of the base, Kb. Solution
The value of Kb for ammonia is 1.8 × 10-5. If 0.25M of ammonia is dissolved, find how much ammonium is formed when ammonia ionizes.
Solution
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
M
Hint Unavailable
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
M
Hint Unavailable
Calculate the pH of the solution.
Solution
pH =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
pH =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Acid Ionization Ka with Triprotic Acids
Phosphoric acid, H3PO4 is a triprotic acid that dissociates fully into phosphate ions. The acid solubility constants are given below.
Ka 1 = 7.5 × 10-3Ka 2 = 6.2 × 10-8
Ka 3 = 2.2 × 10-13
Write the three different dissociation reaction equations of phosphoric acid.
Solution
If the initial concentration of H3PO4 is 0.01 M, calculate the concentration of H2PO4- ions at equilibrium.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
M
Hint Unavailable
Make an ICE table.
You cannot neglect the change in 'x' because the ratio of initial reactant to the k value is greater than 100.
H3PO4 (aq) ↔ H+(aq) H2PO4-(aq)
I 0.01 M 0 mol/L 0 mol/L
C - x + x + x
E 0.01 M - x x x
Use the quadratic equation to solve...
Neglect the negative value, so the [H+] = [H2PO4-] = 0.00569 M.
Hint
Clear
Info
Incorrect Attempts:
CHECK
M
Hint Unavailable
You cannot neglect the change in 'x' because the ratio of initial reactant to the k value is greater than 100.
| H3PO4 (aq) ↔ | H+(aq) | H2PO4-(aq) | |
| I | 0.01 M | 0 mol/L | 0 mol/L |
| C | - x | + x | + x |
| E | 0.01 M - x | x | x |
Neglect the negative value, so the [H+] = [H2PO4-] = 0.00569 M.
Calculate the concentrations of hydrogen phosphate, HPO42- and phosphate, PO43- ions.
Solution
Hint
Clear
Info
[HPO42-] =
× 10
[PO43-] =
× 10
Incorrect Attempts:
CHECK
M
Hint Unavailable
Make the first ICE table for Ka 2.
! Watch out, make sure to use the values calculated previously... [H+] = [H2PO4-] = 0.00569 M.
H2PO4-(aq) ↔ H+(aq) HPO42-(aq)
I 0.00569 M 0.00569 mol/L 0 mol/L
C - x + x + x
E 0.00569 - x 0.00569 - x x
Neglect 'x' because the ratio of the initial reactant to the Ka 2 value is greater than 100.
The concentration, [H+2] = [HPO42-] = 6.2 × 10-8 M.
Now the total proton concentration, [H+] = [H+1] + [H+2] = 0.00569 M + 6.2 × 10-8 M = 0.00569 M.
Make the second ICE table using the values calculated...
HPO42-(aq) ↔ H+(aq) PO43-(aq)
I 6.2 × 10-8 M 0.00569 M 0 mol/L
C - x + x + x
E 6.2 × 10-8 - x 0.00569 - x x
Neglect 'x' because the ratio of the initial reactant to the Ka 3 value is greater than 100.
[PO43-] = 2.4 × 10-18 M.
Hint
Clear
Info
[HPO42-] =
× 10
[PO43-] = × 10
[PO43-] = × 10
Incorrect Attempts:
CHECK
M
Hint Unavailable
! Watch out, make sure to use the values calculated previously... [H+] = [H2PO4-] = 0.00569 M.
| H2PO4-(aq) ↔ | H+(aq) | HPO42-(aq) | |
| I | 0.00569 M | 0.00569 mol/L | 0 mol/L |
| C | - x | + x | + x |
| E | 0.00569 | 0.00569 | x |
Now the total proton concentration, [H+] = [H+1] + [H+2] = 0.00569 M + 6.2 × 10-8 M = 0.00569 M.
Make the second ICE table using the values calculated...
| HPO42-(aq) ↔ | H+(aq) | PO43-(aq) | |
| I | 6.2 × 10-8 M | 0.00569 M | 0 mol/L |
| C | - x | + x | + x |
| E | 6.2 × 10-8 | 0.00569 | x |
Acid Base Titration
In a titration, a neutral pH is reached when in the same container: (More than one answer: check all that apply).
Solution
The main neutral scenario is when:
Moles of acid = moles of base
But if the volume is the same, then it could also be:
Concentration of acid = concentration of base
Equivalence Point
The equivalence point in a solution (in the same container) is reached when the number of moles (or concentration) of H3O+ = OH-
Solution
n·H+(aq) = n·OH-(aq)
If already in same container, then the volume is the same so the concentrations are directly proportional to the number of moles and concentration can be used/compared. But equivalence point is really always when the number of moles in solution are equal.
The equivalence point of an acid and a base will always occur at a pH of 7.
Solution
The equivalence point usually is at a pH of 7.0 but not always...
While many equivalence points are at a pH of 7, particularly when a strong acid and a strong base are reacted, some combinations of weaker acids and bases will not be at 7.
Furthermore for polyprotic acids (H3PO4) and polyhydroxic bases, there are numerous equivalence points. The equivalence point is reached when one form has been reached fully... like once 0% H3PO4 and 100% H2PO4-...
While many equivalence points are at a pH of 7, particularly when a strong acid and a strong base are reacted, some combinations of weaker acids and bases will not be at 7.
Furthermore for polyprotic acids (H3PO4) and polyhydroxic bases, there are numerous equivalence points. The equivalence point is reached when one form has been reached fully... like once 0% H3PO4 and 100% H2PO4-...
Equivalence Point with pH ≠ 7
Answer at least one of the following...
Explain why titrating a weak base like Mg(OH)2 with a strong acid has an equivalence point pH < 7.
Solution
The mole equivalent of acid = the mole equivalent of base at the equivalence point. However this does not necessarily mean that the solution is neutralized at a pH = 7.
The weak base will have a strong conjugate acid, Mg2+ that will slightly react with surrounding water increasing the amount of H+ slightly as follows...
Thus decreasing the pH of the solution slightly.
Explain why titrating a strong base like KOH with a weak acid has an equivalence point pH > 7.
Solution
The mole equivalent of acid = the mole equivalent of base at the equivalence point. However this does not necessarily mean that the solution is neutralized at a pH = 7.
The weak acid will have a strong conjugate base, A- that will slightly react with surrounding water increasing the amount of OH- slightly as follows...
Thus increasing the pH of the solution slightly.
Titration of Mono-Protic Acid and Base
If 10mL of 0.50M NaOH is titrated to the equivalence point with 20mL of HCl, calculate the concentration of acid.
Solution
Ca =
Hint
Clear
Info
Incorrect Attempts:
CHECK
mol/L
Hint Unavailable
nacid = nbase
Vacid∙Cacid = Vbase∙Cbase
The equivalence point is reached when neutral pH = 7.0 when the moles of acid equals the moles of base...
This works since the base is mono-hydroxic, and the acid is mono-protic. (Note that it is not necessary to convert to L here... mL is fine...)
Ca =
Hint
Clear
Info
Incorrect Attempts:
CHECK
mol/L
Hint Unavailable
Vacid∙Cacid = Vbase∙Cbase
The equivalence point is reached when neutral pH = 7.0 when the moles of acid equals the moles of base... This works since the base is mono-hydroxic, and the acid is mono-protic. (Note that it is not necessary to convert to L here... mL is fine...)
Titration of Di-Protic Acid and Base (Normality)
30mL of 1.0M Al(OH)3 is titrated with 2.0M H2SO4. Find the volume of acid required to reach equivalence point.
Solution
V =
Hint
Clear
Info
Incorrect Attempts:
CHECK
mL
Hint Unavailable
Normality of 2.0M H2SO4 = 4.0M
nacid∙(numberacid ions) = nbase∙(numberbase ions)
Vacid∙Cacid∙(numberacid ions) = Vbase∙Cbase∙(numberbase ions)
V =
Hint
Clear
Info
Incorrect Attempts:
CHECK
mL
Hint Unavailable
nacid∙(numberacid ions) = nbase∙(numberbase ions)
Vacid∙Cacid∙(numberacid ions) = Vbase∙Cbase∙(numberbase ions)
Indicators
The indicator molecule itself is an acid or a base.
Solution
An indicator is a molecule that changes its structure when it reacts as an acid or a base and usually leads to a color change.
Acid Base Terms: Endpoint
The endpoint in an acid-base reaction is the point at which
Solution
The endpoint is reached when the indicator changes color. If the endpoint of a certain indicator is reached when pH = 7, then the endpoint is at the same point as the equivalence point. This is not always the case. You should choose the correct indicator for the pH you would like to reach/observe.
There are 100s of different indicators to choose from with many different pH end points between 0 - 14. Some indicators such as Thymol Blue have multiple end points (pH ≈ 3, & 9). The transition of an indicator occurs over a range of pH and is difficult to pinpoint.
There are 100s of different indicators to choose from with many different pH end points between 0 - 14. Some indicators such as Thymol Blue have multiple end points (pH ≈ 3, & 9). The transition of an indicator occurs over a range of pH and is difficult to pinpoint.
Polyprotic Acid pKa
To calculate the pH of a polyprotic acid like H2SO4, the average of the Ka for the first proton dissociation and the Ka for the second proton dissociation, is used.
Solution
The pH is calculated based on the first Ka value since the first dissociation is dissolved much more than the second dissociation.
Ka and pKa
Determine the Ka of a solution with pKa = 12
Solution
Ka =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
Hint Unavailable
pKa = -log(Ka)
...
Ka = 1.0 × 10-12
Ka =
Hint
Clear
Info
× 10
Incorrect Attempts:
CHECK
Hint Unavailable
...
Ka = 1.0 × 10-12
Buffers
Which of the following is not always a characteristic of a good buffer?
Solution
While a pH in the range of 6-8 is good, it is not only this range and there are many buffer than can exist in the lower or higher pH ranges - it depends more on what is being buffered. Although weakly acidic buffers are most common. (The rest of the answer choices are characteristics of buffers).
Describe the result of adding a highly concentrated, strong acid (H-X) to a weak, acidic buffer. The buffer exists in solution as:
Solution
- The weak acid buffer does not dissociate much (because it is weak) and exists mostly as reactant, and very little product.
- The strong acid deprotonates into H+ and consumes the A- dissolved from the buffer to make more of the weak acid buffer HA, plus the dissolved ion X-.
- The plentiful buffer acting as a base neutralizes the strong acid by making it into a much weaker acid.
- The result is that the pH will not change (decrease) much. Buffers are very effective at buffering, or reducing the change in pH.
- The weak acid buffer does not dissociate much (because it is weak) and exists mostly as reactant, and very little product.
- The strong acid deprotonates into H+ and consumes the A- dissolved from the buffer to make more of the weak acid buffer HA, plus the dissolved ion X-.
- The plentiful buffer acting as a base neutralizes the strong acid by making it into a much weaker acid.
- The result is that the pH will not change (decrease) much. Buffers are very effective at buffering, or reducing the change in pH.
Describe the result of adding a highly concentrated, strong base (NaOH) to a weak, acidic buffer. The buffer exists in solution as:
Solution
- The strong base (OH-) will consume the hydronium, H3O+ ions in solution from the buffer... to form more water... neutralized.
- Some salt ions from the base Na+ will remain in solution with the ion from the buffer A-.
- The result is that the pH will not change (incrase) much. Buffers are very effective at buffering, or reducing the change in pH.
- The strong base (OH-) will consume the hydronium, H3O+ ions in solution from the buffer... to form more water... neutralized.
- Some salt ions from the base Na+ will remain in solution with the ion from the buffer A-.
- The result is that the pH will not change (incrase) much. Buffers are very effective at buffering, or reducing the change in pH.
The Henderson-Hasselbach Equation with Buffers
A buffer is made by mixing 0.10M acid [HA] with 0.30M of its conjugate base [A-]. The pKa of this acid [HA] solution is 5.00. Assume that all the acid and base dissociates. If 0.05M of a strong acid is added to the solution, what is the new pH of the solution?
Solution
pH =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
pH =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Flashcards: Acids and Bases
| Define a Brønsted-Lowry acid and base |
| An acid is a proton donor, and a base is a proton acceptor |
| Define a Lewis acid and base |
| An acid is an electron acceptor and a base is an electron donor |
| Is it possible to have a negative pH? |
| Yes |
| (At 25˚C) pH + pOH = |
| 14 |
| (At 25˚C) [OH-][H3O+] = |
| 1 × 10-14 |
| If the pOH of a solution at room temperature is 8.4, is it an acid or a base? |
| pH = 14 - 8.4 = 5.6 (this is an acid) |
| Is it possible to calculate the pH of a given mass of Ca(OH)2 in a given volume of water? |
| Yes |
| The conjugate base of a strong acid is weak or strong? |
| Weak |
| Strong acids dissociate/dissolve more or less than weak acids? |
| More |
| What is equivalence point? |
| The equivalence point in a solution is reached when the number of moles (or concentration) of H3O+ = OH- |
| What are the products of neutralization? |
| A salt and water |
| What are the conjugate base and conjugate acid of water? |
| The conjugate base is OH- and the conjugate acid is H3O+ |
| Can bicarbonate (HCO3-) act as an acid or a base? |
| Yes, this is amphoteric. |
| What is a polyprotic acid? |
| An acid with more than one H+, for instance H2CO3, or H3PO4. |
| What is amphoteric? |
| When a compound can act either as an acid or a base, depending on the acidity/alkalinity of the solution. |
| (At 25˚C) Ka × Kb= |
| 1 × 10-14 |
| What phases are included in Ka and Kb equations? |
| (aq) or (g) (no liquids or solids) |
| What is the general calculation for Kb? |
| Concentration of products divided by concentration of reactants |
| What is a low Ka? |
| weak acid |
| What is a high pKb? |
| strong base |
| What is an endpoint? |
| The point of a titration where the indicator changes color |
| Titration of a weak base with a strong acid would have a pH in what range? |
| less than 7 |
| Titration of a strong base with a strong acid would have a pH in what range? |
| = 7 |
Electrochemistry
Red-Ox Applications
Batteries are one of the most common industrial uses of reduction and oxidation reactions.
Solution
Reduction and oxidation reactions can store and release energy in the form of electric current.
(This is a very hot field in chemical engineering right now for the future of energy storage for example at Tesla motors, Apple computers, etc...)
(This is a very hot field in chemical engineering right now for the future of energy storage for example at Tesla motors, Apple computers, etc...)
The Reaction
A transfer of one or more electrons in a chemical reaction is a redox (an oxidation or reduction) reaction.
Solution
Protons do not get transferred.
Reduction Oxidation
An increase in the oxidation number means the compound gets reduced.
Solution
An increase in the oxidation number means the compound gets oxidized. Note that there is no such thing as a 'reduction number'.
Oxidation States: Simple Ion
Determine the oxidation state (number) of the Calcium product in the following reaction.
Solution
Ca → Ca2+ + 2e-
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Neutral atoms have an oxidation number = 0.
The charge on the product, Ca2+ is +2, so the oxidation number is +2.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The charge on the product, Ca2+ is +2, so the oxidation number is +2.
Oxidation States: Ion to Compound
What is the oxidation state of Iron in the product in the reaction: 2Fe + 3Cl2 → 2FeCl3
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
FeCl3 = Fe3+Cl1-3
The charge on iron is +3.
(Note that the coefficients are not involved in determining final oxidation state).
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The charge on iron is +3.
(Note that the coefficients are not involved in determining final oxidation state).
Determine the change in oxidation state of iron, and hence determine whether iron is oxidized or reduced. [2]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Neutral atoms have an oxidation number = 0. So iron starts with an oxidation number of 0.
The change from 0 --> +3 is an increase in oxidation, so iron is oxidized (loses electrons).
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The change from 0 --> +3 is an increase in oxidation, so iron is oxidized (loses electrons).
Oxidation States: Polyatomic Ion
Determine the oxidation state (number) of Carbon in the following polyatomic ion: C2O42-
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
4 O2- = 4 × (-2) = -8
C2 has a +6 charge, therefore each carbon (C) has a +3 charge, and oxidation state (number).
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Oxidation States: Polyatomic Ion Compound
Determine the oxidation state of Hydrogen in the following polyatomic ion: H2SO4
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The H1+2SO42- molecule is neutral. Therefore the following oxidation states are equal in magnitude, with opposite signs:
Since H1+2 = +2, then each hydrogen (H) is +1.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Oxidation
Oxidation is defined as a(n)
Solution
Remember this for the change in electrons:
Oil Is Loss - Reduction Is Gain
O.I.L. - R.I.G.
(Alternate: L.E.O. - G.E.R.)
(Alternate: L.E.O. - G.E.R.)
Oxidation Reduction and Agents
Check the two statements that apply. In the following reaction Magnesium, Mg... (More than one answer: check all that apply)
Solution
Oxidizing agents get reduced as it goes Mg2+ → Mg.
(remember that reduction is a gain in electrons, O.I.L. - R.I.G.)
(remember that reduction is a gain in electrons, O.I.L. - R.I.G.)
Agents
A reducing agent gets reduced.
Solution
A reducing agent gets oxidized as it loses electrons. (O.I.L. - R.I.G.)
Which of the following statements is true for oxidation, reduction reactions?
Solution
Remember with OIL RIG, or LEO GER...
Loss of electrons occurs during oxidation, which happens to reducing agents.
Gain of electrons occurs during reduction, which happens to oxidizing agents.
The electrons from the reducing agents are always transferred to the oxidizing agent.
Loss of electrons occurs during oxidation, which happens to reducing agents.
Gain of electrons occurs during reduction, which happens to oxidizing agents.
The electrons from the reducing agents are always transferred to the oxidizing agent.
Oxidation Reduction and Agents
Which of the following gets oxidized?
Solution
Think O.I.L. - R.I.G.
Therefore Sodium (Na) is the reducing agent that gets oxidized.
Therefore Sodium (Na) is the reducing agent that gets oxidized.
Reduction-Oxidation Reactions
In reduction-oxidation reactions the metal with the higher electronegativity will be oxidized.
Solution
The metal with the higher electronegativity is the one that attracts electrons and gets reduced.
(However, typically the half-reactions are used to compare the metals and determine which one is reduced and which is oxidized).
This is what drives a galvanic/voltaic cell.
(However, typically the half-reactions are used to compare the metals and determine which one is reduced and which is oxidized).
This is what drives a galvanic/voltaic cell.
It is possible for either non-metals, or metals to be oxidizing agents.
Solution
True, some examples of non-metal oxidizing agents are: F2, H2O2, and N2O/H3O+.
Some examples of metal oxidizing agents are: Co3+, Au3+, and Pt2+.
Some examples of metal oxidizing agents are: Co3+, Au3+, and Pt2+.
Batteries
Batteries are a source of energy as electrolytic cells.
Solution
Batteries are galvanic/voltaic cells when discharging.
Only galvanic/voltaic cells are spontaneous. It is the more electronegative metal that drives the spontaneous reaction that causes electrons to flow from the anode to the cathode.
Electrolytic cells are non-spontaneous and require an input of electricity to drive the red-ox reaction, like when a rechargeable battery is being recharged.
Only galvanic/voltaic cells are spontaneous. It is the more electronegative metal that drives the spontaneous reaction that causes electrons to flow from the anode to the cathode.
Electrolytic cells are non-spontaneous and require an input of electricity to drive the red-ox reaction, like when a rechargeable battery is being recharged.
Galvanic Voltaic Cell
In a galvanic (or voltaic) cell, electrons flow from the anode to the cathode.
Solution
Reduction is occurring at the cathode where the electrons are combined with the cations.
Remember this with: AN OX & RED CAT.
(Oxidation occurs at the anode and reduction occurs at the cathode).
Also note that conventional current (the flow of "positive" charges) is directed from the cathode to the anode.
Remember this with: AN OX & RED CAT.
(Oxidation occurs at the anode and reduction occurs at the cathode).
Also note that conventional current (the flow of "positive" charges) is directed from the cathode to the anode.
In a galvanic (or voltaic) cell, the overall cell potential (E˚) must be positive, and spontaneous.
Solution
- The galvanic/voltaic cell is spontaneous, with +E˚.
- Electrolytic cells are non-spontaneous; they require a power source.
- The galvanic/voltaic cell is spontaneous, with +E˚.
- Electrolytic cells are non-spontaneous; they require a power source.
Galvanic Voltaic Cell
In a galvanic (or voltaic) cell, if the salt bridge or porous membrane was missing from the setup, then the cathode would:
Solution
At the cathode, the cations are being reduced - gaining electrons and depositing solid metal onto the electrode surface. The leftover anions makes the solution negative.
If, for instance, the solution at the cathode consisted of Ag+NO3-, then without a salt bridge, all the Ag+ ions would be used up leaving only negatively charged NO3- ions.
The salt bridge is important because it allows positive and negative ions to balance the charges in the solutions as the redox reactions consume particular ions.
If, for instance, the solution at the cathode consisted of Ag+NO3-, then without a salt bridge, all the Ag+ ions would be used up leaving only negatively charged NO3- ions.
The salt bridge is important because it allows positive and negative ions to balance the charges in the solutions as the redox reactions consume particular ions.
Salt Bridge
If a NaNO3 salt bridge is used, which of the following would occur?
Solution
A salt bridge is used to restore the positive charges that build up in the solution at the anode, and the negative charges that build up in the solution at the cathode.
(While the anode electrode is negative and the cathode electrode is positive, the surrounding solution has opposite charges).
(While the anode electrode is negative and the cathode electrode is positive, the surrounding solution has opposite charges).
Galvanic Voltaic Cell
Given the setup in the galvanic/voltaic cell below, which of the following gets reduced?
Solution
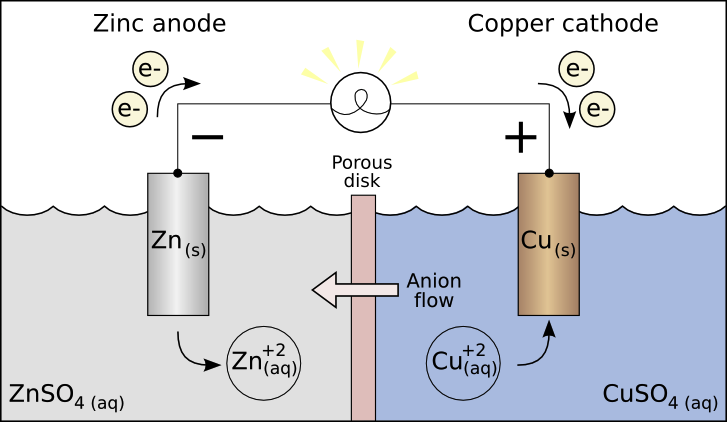
Use the following to remember: reduction occurs at the cathode, oxidation occurs at the anode.
R.E.D. - C.A.T.
A.N. - O.X.
Zn(s) + Cu2+(aq) --> Zn2+(aq) + Cu(s)
R.E.D. - C.A.T.
A.N. - O.X. Zn(s) + Cu2+(aq) --> Zn2+(aq) + Cu(s)
If the salt bridge stopped working, what charges would build up in the solution at the anode? [1]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Positive charges (due to the Zn2+ accumulating) would build up at the anode.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
When aluminum foil is placed over (salty, conductive) lasagna in a stainless steel pan, a galvanic/voltaic electrochemical cell is created. Given the reduction potentials below, determine what will corrode. Yes, a lasagna cell is a real thing. [1]
Solution
E˚red Aluminum = –1.66 V
E˚red Stainless Steel (Type 304, passive) = -0.08 V
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
- Understand that in a galvanic/voltaic cell the anode corrodes as it loses electrons to the cathode, forming dissociated cations.
- The highest E˚red gets reduced (-0.08 V) making it the cathode.
- Stainless steel is the cathode... Aluminum foil the anode.
- Therefore the aluminum foil corrodes.

Lasagna Cell (Creative Commons Credit: Flickr - Tom Arthur)
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
- Understand that in a galvanic/voltaic cell the anode corrodes as it loses electrons to the cathode, forming dissociated cations.
- The highest E˚red gets reduced (-0.08 V) making it the cathode.
- Stainless steel is the cathode... Aluminum foil the anode.
- Therefore the aluminum foil corrodes.
 |
Electrolytic Cells
Electrolytic cells are spontaneous.
Solution
Electrolytic cells are non-spontaneous. Electrolytic cells must be connected to a power source to drive the reaction.
Which of the following reactions could occur in an electrolytic cell, but would be unlikely to occur in a galvanic or voltaic cell?
Solution
Galvanic or voltaic cell require spontaneous reactions, for instance the reduction of a halogen, or the oxidation of an alkali earth metal.
Of the reactions here, the least likely to occur spontaneously is the reduction of Lithium (Li).
Of the reactions here, the least likely to occur spontaneously is the reduction of Lithium (Li).
The Standard H2 Half Cell
The standard H2 half cell has a potential equal to ___ Volts, and involves H2 gas bubbled over a ________ electrode in 1.0M hydrochloric acid, at SATP (25˚C, 100kPa).
Solution
A Standard Hydrogen Half Cell Reaction has a platinum electrode and bubbles hydrogen gas over it as protons are released into solution, with chloride ions.
The EMF (cell potential) of this is always 0.00
The EMF (cell potential) of this is always 0.00
Measuring Cell Potential
The only way to measure the cell potential (Voltage) of a certain reduction or oxidation reaction is to experimentally measure it by combining it with the standard H2 half cell reference of 0 volts.
Solution
Because in a lab, there needs to be both an anode and an cathode. The standard H2 half cell fills in for either the anode or cathode, depending on the main half-reaction that is being analyzed.
Cell Potential
For the reverse of the following reaction, E˚ = +0.44 V
Solution
Change the sign when the half-reaction is reversed.
The E˚ values for the following two reactions are identical.
Solution
True because the E˚ potential for hydrogen is always 0.000 V
Cell Potential
Which three of the following overall reactions are spontaneous?
Solution
Positive cell potentials mean the reactions are spontaneous. Note that it is the overall (Ecell) cell potential and not the half-cell potential (E˚) that determines if a reaction is spontaneous.
Cell Potential
A negative cell potential (E˚) indicates that the cell is galvanic or voltaic.
Solution
An overall cell potential (2 half-reactions combined) that is negative indicates a non-spontaneous cell, which would not produce current like a galvanic or voltaic cell - rather it would be electrolytic.
E˚cell > 0.00 --> SPONTANEOUS (galvanic/voltaic)
E˚cell = 0.00 --> At equlibrium
E˚cell < 0.00 --> Non-spontanous (electrolytic)
E˚cell = 0.00 --> At equlibrium
E˚cell < 0.00 --> Non-spontanous (electrolytic)
Ions and Oxidation
Which of the following is most easily oxidized?
Solution
Oxidation is a loss of electrons, and atoms that give up electrons most easily are more easily oxidized. Think of the periodic trends that affect this: electronegativity, ionization energy, electron affinity, atomic radius, and nuclear charge. The elements with lower electronegativity will be oxidized more easily. Conversely, atoms with higher electronegativity will tend to be reduced. Of the elements given, the most electronegative alkali earth metal is most easily oxidized - this is Rubidium, Rb.
Also, looking at a table of the redox E˚ cell potentials, Rubidum is the most negative (-2.98 V), and therefore is most easily oxidized.
Also, looking at a table of the redox E˚ cell potentials, Rubidum is the most negative (-2.98 V), and therefore is most easily oxidized.
The Electrochemistry of Corrosion
The rust that builds up on steel and iron is made of a compound called iron(III) oxide (Fe2O3). Electrons get transferred from one type of element to another, based on electronegativity difference. Which of the following gets oxidized when rust forms?
Solution
Oxidation is a loss of electrons.
Iron, Fe loses electrons to form the ion Fe3+.
Iron, Fe loses electrons to form the ion Fe3+.
Cell Potentials
Use the electrochemical series for the following questions.
| Half-Reaction | E˚ (Volts) | |
| -3.05 | ↑ oxidized (reducing agent) | |
| -2.92 | ||
| -2.71 | ||
| -0.41 | ||
| 0.00 | ||
| +0.34 | ||
| +0.80 | ||
| +1.09 | ||
| +1.36 | ||
| +1.84 | ↓ reduced (oxidizing agent) |
Half-reactions with more positive E˚ values:
Solution
By default the half-reactions are always written and compared in the reduction direction, and it is up to us to reverse the direction for oxidation reactions.
Which of the following reactions will not occur spontaneously?
Solution
Compare the ranking of the elements in the reaction on the electrochemical series. If the cation is higher (E˚ more positive) then there is no reaction.
Iron (Fe) is higher on the electrochemical series than copper (Cu) so iron gets oxidized and loses electrons.
Since iron has already lost electrons (Fe2+) it cannot undergo a reaction.
Iron (Fe) is higher on the electrochemical series than copper (Cu) so iron gets oxidized and loses electrons.
Since iron has already lost electrons (Fe2+) it cannot undergo a reaction.
Half-Reactions and Cell Potential
A certain cell potential combines a strong oxidation half-reaction, along with the following reduction reaction. To calculate the overall cell potential, in Volts, we must multiply the E˚ value by a factor of 3 in one of the steps.
Solution
E˚ cell calculations don't involve multiplying by a coefficient. The only thing we must watch out for are the signs (+ or -) and which half-reaction gets oxidized or reduced.
Compare Half-Reaction (E˚) Potentials
Given the following spontaneous, oxidation-reduction reactions,
Order the 4 reducing agents from weakest to strongest (top to bottom).
Solution
Cu
Fe
Ag
Na
Reducing agents get oxidized (lose electrons) to the stronger oxidizing agent, like a tug-of-war. The strongest reducing agent will lose its electrons to everything. Comparing the (E˚) potentials...
[weakest reducing agent] Ag < Cu < Fe < Na [strongest reducing agent]
Sodium (Na) loses electrons to everything here... and is the strongest reducing agent out of the ones here.
Cu
Fe
Ag
Na
Match the reducing or oxidizing agents with the correct half-reaction cell potential.
Solution
Na+
Fe2+
Cu2+
Ag+
E˚(red) = +0.34 V
E˚(red) = -0.41 V
E˚(red) = +0.80 V
E˚(red) = -2.71 V
The E˚(red) values of half-reactions show relative strength or red/ox.
The strongest oxidizing agent (gets reduced) has the highest +E˚(red). The strongest reducing agent (gets oxidized) has the lowest -E˚.
[weakest reducing agent] Ag < Cu < Fe < Na [strongest reducing agent]
Na+
Fe2+
Cu2+
Ag+
E˚(red) = +0.34 V
E˚(red) = -0.41 V
E˚(red) = +0.80 V
E˚(red) = -2.71 V
The strongest oxidizing agent (gets reduced) has the highest +E˚(red). The strongest reducing agent (gets oxidized) has the lowest -E˚. [weakest reducing agent] Ag < Cu < Fe < Na [strongest reducing agent]
Explain why there would be no reaction below. [2]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
This reaction is non-spontaneous and will not occur by itself because copper is the stronger oxidizing agent and tends to get reduced, holding onto its electrons, rather than giving them to Fe2+. The larger E˚(red) tends to get reduced.
E˚(red) Copper = +0.34 V
E˚(red) Iron = -0.41 V
Therefore the reduction of iron will not occur spontaneously.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
E˚(red) Iron = -0.41 V Therefore the reduction of iron will not occur spontaneously.
Calculate Cell Potential Given Half-Reaction (E˚) Potentials
The standard electrode potentials for two half reactions are listed below.
Solution
Determine the EMF, (cell potential, in volts) for the following reaction when the half-cells are connected.
Hint
Clear
Info
Incorrect Attempts:
CHECK
V
Hint Unavailable
The larger E˚ gets reduced.
Simply use this without switching the equation directions:
E˚ Cell = E˚(Red) - E˚(Ox)
(Don't multiply by any coefficients)
Or use this if you switch the direction of the half-reaction that gets oxidized and reverse its sign:
E˚ Cell = E˚(Cathode) + E˚(Anode)
Hint
Clear
Info
Incorrect Attempts:
CHECK
V
Hint Unavailable
Simply use this without switching the equation directions:
E˚ Cell = E˚(Red) - E˚(Ox) (Don't multiply by any coefficients)
Or use this if you switch the direction of the half-reaction that gets oxidized and reverse its sign:
E˚ Cell = E˚(Cathode) + E˚(Anode)
Calculate Cell Potential Given Half-Reaction (E˚) Potentials
The standard electrode potentials for two half reactions are listed below.
Solution
What is the cell potential (in volts) for the following reaction when the half-cells are connected?
Hint
Clear
Info
Incorrect Attempts:
CHECK
V
Hint Unavailable
The larger E˚ value gets reduced... +0.80 V
Simply use this without switching the equation directions:
E˚ Cell = E˚(Red) - E˚(Ox)
= +0.80 V - (+0.35 V)
= 0.45 V
(Don't multiply by any coefficients)
Or, use this if you switch the direction of the half-reaction that gets oxidized and reverse its sign:
E˚ Cell = E˚(Cathode) + E˚(Anode)
= +0.80 V + (-0.35 V)
= 0.45 V
Hint
Clear
Info
Incorrect Attempts:
CHECK
V
Hint Unavailable
Simply use this without switching the equation directions:
E˚ Cell = E˚(Red) - E˚(Ox)
= +0.80 V - (+0.35 V)
= 0.45 V
(Don't multiply by any coefficients)
Or, use this if you switch the direction of the half-reaction that gets oxidized and reverse its sign:
E˚ Cell = E˚(Cathode) + E˚(Anode)
= +0.80 V + (-0.35 V)
= 0.45 V
Calculate Cell Potential Given Half-Reaction (E˚) Potentials
The standard electrode potentials for two half reactions are listed below.
Solution
What is the cell potential (in volts) for the following reaction when the half-cells are connected?
Hint
Clear
Info
Incorrect Attempts:
CHECK
V
Hint Unavailable
The larger E˚ value gets reduced.
Simply use this without switching the equation directions:
E˚ Cell = E˚(Red) - E˚(Ox)
= -0.44 V - -1.68 V
= + 1.24 V
(Don't multiply by any coefficients)
Or, use this if you switch the direction of the half-reaction that gets oxidized and reverse its sign:
E˚ Cell = E˚(Cathode) + E˚(Anode)
= -0.44 V + 1.68 V
= + 1.24 V
Hint
Clear
Info
Incorrect Attempts:
CHECK
V
Hint Unavailable
Simply use this without switching the equation directions:
E˚ Cell = E˚(Red) - E˚(Ox)
= -0.44 V - -1.68 V
= + 1.24 V
(Don't multiply by any coefficients)
Or, use this if you switch the direction of the half-reaction that gets oxidized and reverse its sign:
E˚ Cell = E˚(Cathode) + E˚(Anode)
= -0.44 V + 1.68 V
= + 1.24 V
Electrochemical Cell Short-form Notation
Which of the following is the anode electrode?
Solution
The anode is the whole left side, whereas the anode electrode is the solid metal on the left side. This short-form notation always displays the anode on the left side and the cathode on the right side.
The single vertical line represents a difference between phases (solid and aqueous) while the double bar indicates separate cells (anode and cathode) connected with a salt bridge or porous membrane.
The single vertical line represents a difference between phases (solid and aqueous) while the double bar indicates separate cells (anode and cathode) connected with a salt bridge or porous membrane.
The anode is always on the left side and the cathode is always on the right side.
Solution
True, and the electrons flow from the left (negative anode) to the right side (positive cathode).
Which side would you expect to have the larger E˚(red) value? [1]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Since reduction occurs at the cathode (RED CAT, AN OX), then the right-hand cathode side would be reduced.
Reduction half-reactions are larger numbers, so the Copper would have the larger E˚(red) value.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Reduction half-reactions are larger numbers, so the Copper would have the larger E˚(red) value.
Electrochemical Cell Short-form Notation
What gets reduced?
Solution
Anode (left), cathode (right).
Reduction occurs at the cathode, and is a gain of electrons. The Cu2+ gains the electrons (gets reduced).
Reduction occurs at the cathode, and is a gain of electrons. The Cu2+ gains the electrons (gets reduced).
Given the half-reaction reduction potential, calculate the EMF (E˚) of the cell.
Solution
Co2+(aq) + 2e- --> Co(s) = -0.28 V
Hint
Clear
Info
Incorrect Attempts:
CHECK
V
Hint Unavailable
Since the anode is on the left, the Cobalt gets oxidized.
Remember the hydrogen half-reaction always has a cell potential E˚ = 0.00
Hint
Clear
Info
Incorrect Attempts:
CHECK
V
Hint Unavailable
Electroplating
Electroplating uses electrical current to drive red-ox reactions and reduce dissolved metal cations, to form a solid metal layer over an other metal.

In this setup, copper is the...
Solution
Electrolytic cells have positive anodes. You can see in the diagram that the positive terminal of the power source is connected to the anode.


In this setup, which electrode gets consumed as its atoms form cations that get transferred to the opposite electrode?
Solution
The copper plating metal at the positive anode gets consumed as it is oxidized and dissociates. The Cu2+ is carried by the solute to coat the metal when the cation gets reduced at the negative cathode.


You don't want your bare chromoly steel (4130, Cr, Mo, C, Fe) bicycle frame to rust so you decide to do a cool summer project to electroplate it in copper to prevent rusting, rather than just paint it (boring). You choose copper because it doesn't rust and is the cheapest plating metal available to you. Describe, in brief, the procedure for setting up the electroplating system.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
- Clean the bike frame from dirt and grease and connect it to the negative power terminal - this is the cathode.
- Connect a bunch of copper to the positive terminal to make anodes.
- Bath the anode and cathode in copper(II) sulfate solution.
- Dip the frame and let it sit for a while...
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
- Clean the bike frame from dirt and grease and connect it to the negative power terminal - this is the cathode.
- Connect a bunch of copper to the positive terminal to make anodes.
- Bath the anode and cathode in copper(II) sulfate solution.
- Dip the frame and let it sit for a while...
Electrochemical Mistake
As an engineer you know that when different metals are in electrical contact, the anode will slowly erode over time like in the picture below. If you must combine two different metals and you want to minimize erosion/corrosion of metal, which two would you choose to put together? Solution
 |
It is ideal to use the exact same metal everywhere, but if two different metals must be in contact, then you should choose the two with the closest reduction potentials...
300 series stainless steel, E˚red = -0.50 V,
brass alloy, E˚red = -0.45 V
300 series stainless steel, E˚red = -0.50 V,
brass alloy, E˚red = -0.45 V
Electrochemical Cell Applications
The most common form of tarnish on silver is silver sulfide, rather than silver oxide. Tarnished silver can be polished in a bath of salts and baking soda (electrolytes) while in contact with certain other metals.
E˚red Ag2S = -0.691 VGiven the reduction potentials, determine the best metal to use for polishing tarnished silver.
Solution
You still need the Ag+2S2- to be reduced to Ag(s).
2Ag+ + 2e- → 2 Ag (reduced, gained e-)
Reduction occurs at the cathode. For silver to be reduced, it must be with a different metal with a lower reduction potential to make the silver reduced and the cathode. The lower the reduction potential the stronger the reaction...
Aluminum, E˚red = -1.66 V
Aluminum, E˚red = -1.66 V
Now for a relatively fast setup, you connect a copper electrode to one terminal, and the tarnished silver to a different terminal of a battery. Determine which side of the battery to connect the tarnished silver to, and predict what electrode this will be. [2]
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
You need the Ag+2S2- to be reduced to Ag(s).
2Ag+ + 2e- → 2 Ag (reduced, gained e-)
- In an electrolytic cell, reduction still occurs at the cathode like galvanic/voltaic, except this time the cathode is negative.
- The oxidation still occurs at the anode, but the anode is positive in electrolytic cells.
- The copper loses electrons, which flow through the electrolyte baking soda solution, to the surface of the tarnished silver. (It is not that important to use copper in an electrolytic cell, other metals like tin or iron could be used)
- The silver quickly gains the electrons, attached to the negative battery terminal, and reduces at the cathode to the polished/shiny state.
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
- In an electrolytic cell, reduction still occurs at the cathode like galvanic/voltaic, except this time the cathode is negative.
- The oxidation still occurs at the anode, but the anode is positive in electrolytic cells.
- The copper loses electrons, which flow through the electrolyte baking soda solution, to the surface of the tarnished silver. (It is not that important to use copper in an electrolytic cell, other metals like tin or iron could be used)
- The silver quickly gains the electrons, attached to the negative battery terminal, and reduces at the cathode to the polished/shiny state.
Cathodic Protection
Cathodic protection is a technique used in industry on ships, pipelines, oil platforms, bridges, and other structures. See the white metal bar screwed onto the ship hull, below.
 |
Simply supplying additional electrons (negative charge) to steel/iron in a non-conductive environment like air would be enough to provide the steel/iron with cathodic protection to prevent rusting.
Solution
Additional electrons from a power source would prevent corrosion (oxidation, loss of electrons) to the steel/iron. The negatively charged steel/iron would tend more towards a cathode rather than dissolving apart as an anode.
Cathodic protection places a stronger reducing agent like zinc, near iron so that the iron becomes the anode of an electrochemical cell.
Solution
Cathodic protection places a stronger reducing agent like zinc, which preferentially gets oxidized rather than iron. The iron becomes the cathode of an electrochemical cell. When iron rusts, it is because the iron is acting as the anode and Hydrogen and or Oxygen is acting as the cathode.
Fe3+ has E˚red = -0.04
Zn2+ has E˚red = -0.76
Therefore the iron gets reduced and the zinc gets oxidized.
With cathodic protection, you want the zinc to be sacrificed/oxidized first (preferentially) rather than the iron.
Fe3+ has E˚red = -0.04
Zn2+ has E˚red = -0.76
Therefore the iron gets reduced and the zinc gets oxidized.
With cathodic protection, you want the zinc to be sacrificed/oxidized first (preferentially) rather than the iron.
Given the reduction potentials, determine which metal would provide the best cathodic protection with iron(III), E˚red = -0.04 V.
Solution
Magnesium is the most active reducing agent (gets oxidized) because it has lowest reduction potential. Remember that the highest reduction potential is the cathode and the lowest reduction potential is the anode.
Flashcards: Reduction, Oxidation
| A loss of electrons is _________________. |
| Oxidation (OIL RIG) |
| A gain of electrons is _________________. |
| Reduction (OIL RIG) |
| What happens to a reducing agent in a redox reaction? |
| It gets oxidized (because it gains electrons, which reduces a different compound) |
| What happens to an oxidizing agent in a redox reaction? |
| It gets reduced (because it loses electrons, which oxidizes a different compound) |
| An decrease in the oxidation number means the compound gets ___________. |
| Reduced (gain in electrons) (e.g. +1 → -1, or +3 → +1, etc...) |
| What is the oxidation number of Magnesium and the other group 2 elements? Mg → Mg2+ + 2e- |
| +2 (group 2 elements oxidize, lose 2 electrons) |
| What is the oxidation number of diatomic molecules and noble gases? |
| 0 |
| What is the oxidation number of halogens? |
| -1 |
| As iron (II) rusts from Fe to FeO, is it oxidized or reduced? |
| Iron goes from Fe → Fe2+, therefore it loses electrons and is oxidized. |
| What is the oxidation number of iron in FeCl3? |
| +3 |
| Since oxygen has a -2 oxidation number, what is the oxidation state of carbon in CO32-? |
| +4 |
| Which of the following gets reduced? |
| Al3+ (OIL RIG - reduction is gain of electrons: Al → Al3+) |
| Of the group 1, 2, 17, and 18 elements, which tends to be more easily reduced? |
| Group 17 elements. (OIL RIG - reduction is gain of electrons) |
| Which of the following is the reducing agent? |
| Na |
| In reduction-oxidation reactions the metal with the lower electronegativity get: |
| Oxidized E.g. K → K+ Elements with low EN tend to lose electrons - get oxidized |
| Which electrode is negatively charged? |
| Anode |
| What is the function of the salt bridge? |
| The salt bridge maintains an even charge balance in the solutions at the cathode and at the anode side |
| What occurs at the anode and at the cathode? |
| Oxidation occurs at the anode and reduction occurs at the cathode (Remember: AN OX, RED CAT) |
| What type of cell consumes energy, and what type produces energy? |
| Electrolytic cells consume energy and galvanic/voltaic cells produce energy |
| Given a Zinc anode and a Copper cathode, which gets reduced? |
| Reduction occurs at the cathode, where Cu2+(aq) ions in solution solidify into Cu(s). (OIL RIG - reduction is gain of e-) |
| Determine which is the anode electrode, anode solution, cathode electrode, and cathode solution: |
| The diagram always follows: |
| What is the charge on the cathode in an electrolytic cell? |
| Reduction always occurs at the cathode, so for the reaction (Cu2+ + 2e- → Cu) to occur at the cathode, the cathode must be negatively charged. |
| Which will be reduced? A half reaction with a cell potential E˚ = -3.5 compared to another half reaction with a cell potential E˚ = +0.9 |
| E˚ = +0.9 (Half-reactions with more positive E˚ values get reduced and are better oxidizing agents) |
