GRADE
11
Math: Functions and Relations MCR3U
TABLE OF CONTENTS
Exponent Laws
| Specific Topic | General Topic | School | Date |
|---|---|---|---|
| Exponent Laws | Fractions, Negatives, Roots | Bayview | Nov 2013 |
| Exponent Laws | Decimals, Negatives | Bayview | Nov 2013 |
Review of the Basics: Product Rule
Write each with a single, positive exponent, showing your work without using a calculator.
xa × xb = xa + b
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= 37
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= 52 + (-2)
= 50
= 1
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
= 50
= 1
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= (-10)-5 + 7
= (-10)2
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
= (-10)2
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Review of the Basics: Quotient Rule
Simplify, showing your work without using a calculator.
xa ÷ xb = xa - b
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= 77 - 3
= 74
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
= 74
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= (-2) -11
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= (-5)6 - (-4)
= (-5)10
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
= (-5)10
Review of the Basics: Power of a Power
Write each with a single, positive exponent, or reduced fraction, showing your work without using a calculator.
(xa)b = xa × b
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= 32 × 4
= 38
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
= 38
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
= 22 × 3
= 26
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
= 26
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
22 × 3 × 2
= 212
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
= 212
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Review of the Basics: Negative Powers
Simplify fully to an integer or fraction using positive exponents, showing your work without using a calculator.
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
New Law: Rational Exponents & Roots/Radicals
Write each with a single positive exponent, or an integer, or a reduced fraction, where applicable. (Without using a calculator)
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
━━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
━━━
Incorrect Attempts:
CHECK
Hint Unavailable
Rational Expressions with Exponent Laws
Simplify fully, using positive exponents.
Click to show Exponent Laws Solution
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
(3)(2)x3 + 4 + (-2)
= (6)x7 - 2
= 6x5
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
= (6)x7 - 2
= 6x5
Solution
Hint
Clear
Info
━━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
Hint
Clear
Info
━━━━━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Roots and Radicals
Simplify given two of the most basic rules for roots.
Simplify the root, by dragging the steps into the correct order.
Solution
Find the greatest perfect square (like 82) under the root to bring it out.
Simplify .
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Roots and Radicals
Simplify fully without the use of a calculator, leaving your answer in root form.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Add roots that have the same base underneath similar to adding like variables,
for example 3x + 4x = 7x...
for example 3x + 4x = 7x...
Simplify fully without the use of a calculator, leaving your answer in root form.
Solution
You would simplify the first, but it is shown the other way here for the sake of learning...
Simplify fully without the use of a calculator, leaving your answer in root form.
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Roots and Radicals
Simplify fully without the use of a calculator, leaving your answer in root form.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Practice with Exponent Laws
Write each with a single positive exponent, or integer, or reduced fraction, showing your work without using a calculator.
Solution
Video
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
Video
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
FOIL:
Functions
Function Output
ƒ(x) = x2 is the same as y = x2
Solution
In function notation, ƒ(x) is a way of representing 'y'. Furthermore the function notation ƒ(x) shows the certain 'x' value that is plugged into the function to obtain the value of 'y'.
Input and Output Notation of a Function
It is important to make the distinction between the input and output of a function.
The output of the following functions would be the same.
Solution
ƒ(2) = x2 + 2x ƒ(2) = n2 + 2n y = x2 + 2x
Any input would result in the same output regardless of the different variables used in the functions: x2 + 2x and n2 + 2n
Function notation uses ƒ(x) instead of y, but they mean the same thing. Think of ƒ(x) as just, y.
Function notation is useful to show substitutions, for example:
(2, 8)
Function notation uses ƒ(x) instead of y, but they mean the same thing. Think of ƒ(x) as just, y.
Function notation is useful to show substitutions, for example: (2, 8)
Which output is true for the function ƒ(x) = 3x2
Solution
ƒ(2) = 12
- (2) is the input of the independent variable
- 12 is the output of the dependent variable
- (2) is the input of the independent variable
- 12 is the output of the dependent variable
The input in the following function is:
Solution
The input of the independent variable is the (3)...
Evaluate.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Using function notation, sub the x-value (x = 4) into the function:
So, ƒ(4) = 18, or y = 18...
In the function below, x is the dependent variable and y is the independent variable.
Solution
y = 3x2 + 1
It is the other way around.
x is the independent variable and y is the dependent variable.
x is the independent variable and y is the dependent variable.
Ordered Pairs
Which of the following is an ordered pair for the function: ƒ(x) = 2x2 - 4x
Solution
An ordered pair is a coordinate, or basically a point on the graph.
Just plug a given x-value and check which y-value is correct for the given x-value.
Just plug a given x-value and check which y-value is correct for the given x-value.
Functions: Vertical Line Test
A function cannot have:
Solution
Functions Cannot Have 2 Different Outputs for the Same Input
Which of the following is not a function?
Solution
Function Notation
Given the function below, determine ƒ. Reduce fully.
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Given the function ƒ(x) = x2 - 3x - 6, determine: 3ƒ(2) + 1
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Given the function y = 3ƒ[-4x + 2] + 7, the image formed from the point (-1, 2) is calculated with,
y = 3[-4(-1) + 2] + 7, which is (-1, 25).
Solution
False. Do not just plug the 'x' value into the function notation. See next question for the correct process.
Given the function below, determine the image formed from the point (-2, 5).
Solution
y = -4ƒ[-3x - 12] - 2
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
This is based on the general function,
y = aƒ[k(x - c)] + d
Write in function notation, and remember the 'c' value technically should be written as subtracted...
Where:
- a = -4
- k = -3
- c = -12 (careful here!)
- d = -2
- 'x' is affected by 'k' and 'c' = k(x) + c
- 'y' is affected by 'a' and 'd' = a(y) + d
A common mistake is to apply 'c' before 'k', and 'd' before 'a'. Make sure to do it in the correct order,
The point is (6, -22).
- a = -4
- k = -3
- c = -12 (careful here!)
- d = -2
- 'x' is affected by 'k' and 'c' = k(x) + c
- 'y' is affected by 'a' and 'd' = a(y) + d
Review from Grade 10: Factoring Trinomials when a = 1
Factor fully.
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Review from Grade 10: Factoring Trinomials when a ≠ 1
Factor by decomposition, or directly (if you are able).
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
What multiplies to (2)(6) = 12? ==> -12 and -1
What adds to -13? ==> -12 and -1
What adds to -13? ==> -12 and -1
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
What multiplies to (10)(6) = 60? ==> 5 and 12
What adds to 17? ==> 5 and 12
What adds to 17? ==> 5 and 12
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Review from Grade 10: Factoring Trinomials when a = 1, and x4
Factor using any method.
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
There are two rounds of differences of squares in here...
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Review from Grade 10: Common Factoring (and Factoring)
Factor fully. (Keep your answer in the same order as the terms in the question, and don't write unnecessary exponents like x1)
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
Common factor out the highest factor of the coefficients, which is 2.
Then common factor the highest degree of x out of all terms, which is x1.
Then common factor out the highest degree of y out of all terms, which is y1.
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Then common factor the highest degree of x out of all terms, which is x1.
Then common factor out the highest degree of y out of all terms, which is y1.
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
Then notice that (4x2 - y2) can be factored even further as a difference of squares:
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
First common factor
Then factor the trinomial:
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Difference of Squares
Which of the following functions is a Difference of Squares?
Solution
A difference of squares is made of two things:
1) Subtraction (difference) between two terms.
2) Terms that are perfect squares.
1) Subtraction (difference) between two terms.
2) Terms that are perfect squares.
Factoring: Difference of Squares and Fractions
Factor fully.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Tricky Factoring
Factor fully.
x2 - y2 + 4y - 4
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
See that you can factor the last three terms -(y2 - 4y + 4)...
16x2 - 72x + 81 - 9y2 + 12y - 4
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
See that you can factor the first 3 terms, and separately factor the last 3 terms.
Domain and Range: Linear Function
State the domain and range of the parent function: Solution
Domain and Range
State the domain of the set:
Solution
{-4, -3, -2, -1, 0, 1, 2}
using set notation: {X | -4 ≤ x ≤ 2 }
Inverse Graphs
The graph of an inverse equation compared to the original function is a reflection on:
Solution
The line y = x
Inverse Equations
Determine the inverse of the following equations.
Solution
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Properties of the Inverse of a Function
Determine the inverse of the set: {(1, -4), (2, -6), (3, -8), (4, -10)}
Solution
The 'x' and 'y' values switch for the inverse.
So, {(1, -4), (2, -6), (3, -8), (4, -10)}... becomes, {(-4, 1), (-6, 2), (-8, 3), (-10, 4)}
So, {(1, -4), (2, -6), (3, -8), (4, -10)}... becomes, {(-4, 1), (-6, 2), (-8, 3), (-10, 4)}
Properties of the Inverse of a Function
State the domain and range of the inverse ƒ(x)-1 of the set {(1, 2), (-3, 3), (7, 5), (3, -4)}
Solution
Inverse of Absolute Value Function
What range will make the inverse of ƒ(x) = 3|x + 1| a function?
Solution
All values of x are positive from the point (0, -1).
Transformations
Which of the following functions has a (horizontal) reflection in the y-axis from its parent function?
Solution
Horizontal reflections occur for ƒ(-x)...
See graph of:
This has a vertical reflection, a horizontal compression by 0.5, and a horizontal shift 0.5 right.
Note that a vertical reflection occurs for -ƒ(x), which would have a negative outside of the brackets... ...
See graph of:
This has a vertical reflection, a horizontal compression by 0.5, and a horizontal shift 0.5 right.
Note that a vertical reflection occurs for -ƒ(x), which would have a negative outside of the brackets... ...
Equations in Vertex Form
Given the general form of a quadratic, determine the equation of a quadratic function with the transformations listed below....
Reflection in the x-axis, vertical stretch by a factor of 3, vertical translation 5 units up.
Solution
A parabola with vertex at (-1, 3), opening upward, and with a vertical compression by a factor of ⅛.
Solution
Finding the Vertex by Completing the Square
Determine the vertex for each of the following by completing the square.
ƒ(x) = -3x2 + 9x - 1
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
ƒ(x) = -2x2 + 8x + 4
Solution
Hint
Clear
Info
( , )
Incorrect Attempts:
CHECK
Hint Unavailable
(2, 12)
Finding the Vertex by Completing the Square (With Fractions!)
Determine the vertex for each of the following by completing the square (without decimals).
y = -3x2 + 5x - 2
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
ƒ(x) = ⅕x2 + 2x + 4
Solution
Hint
Clear
Info
( , )
Incorrect Attempts:
CHECK
Hint Unavailable
(-5, 1)
Finding the Vertex Using Symmetry
Solve for the vertex of the following function, using symmetry: ƒ(x) = x2 + 6x + 5
Solution
Hint
Clear
Info
( , )
Incorrect Attempts:
CHECK
Hint Unavailable
Roots (x-intercepts) of Quadratics
Determine the roots of the following function. State the lower root first.
ƒ(x) = -2(x + 3)2 - 12
Solution
Hint
Clear
Info
( , ) & ( , )
Incorrect Attempts:
CHECK
Hint Unavailable
The roots are located at: (-2, 0) and (8, 0).
Determining Number of Points of Intersections with Discriminant
Determine if the functions intersect 0, 1, or 2 times: and
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Set the equations equal and rearrange into standard form: ax2 + bx + c = 0
Plug this in and determine the sign of the discriminant...
Since the discriminant is positive, there are 2 points of intersection (POI).
(negative means no POI, and equals zero means 1 POI)
(negative means no POI, and equals zero means 1 POI)
Determine the value of 'k' where there is 1 point of intersection: and
Solution
k =
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Set the equations equal and rearrange into standard form: ax2 + bx + c = 0
Plug this in and determine the sign of the discriminant... a = 6, b = -2, c = (-4 - k)
Determining Number of Points of Intersections with Discriminant
Determine the value of 'n' where the functions intersect once: and
Solution
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Set the equations equal and rearrange into standard form: ax2 + bx + c = 0
Where a = 2, b = 0, and c = (-3 + n)
Plug this in and set the discriminant equal to zero to determine 'n' with 1 intersection...
Therefore 'n' equals 3 when there is one intersection... y = 4x - 3
Plug this in and set the discriminant equal to zero to determine 'n' with 1 intersection... Therefore 'n' equals 3 when there is one intersection... y = 4x - 3
Determining Number of Points of Intersections with Discriminant
The discriminant can be used to determine the number of points of intersection without a quadratic, for example between the equations below...
Solution
The discriminant must be used with at least one quadratic equation because it was derived from the quadratic equation (shown in a different question).
Rational Expressions
Manipulating Expressions
Simplify.
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The following steps are correct.
Solution
You cannot 'add' or 'subtract' this part below...
Instead, it must be 'multiplication' or 'division', so you could multiply things, like...
Solution
Hint
Clear
Info
━━━
Incorrect Attempts:
CHECK
Hint Unavailable
Make a common denominator first.
Solution
Hint
Clear
Info
━━━━━━
Incorrect Attempts:
CHECK
Hint Unavailable
Make a common denominator first.
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Rational Expressions with Multiplication and Division of Monomials
Simplify (and state the restrictions in your notes - answer enter not available).
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
a ≠ 0, b ≠ 0
(Even though 'b' cancels, you still have to state the restriction on it. (Any variable that was ever in the denominator has a restriction).
(Even though 'b' cancels, you still have to state the restriction on it. (Any variable that was ever in the denominator has a restriction).
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
a ≠ 0, b ≠ 0
(Even though 'b' cancels, you still have to state the restriction on it. (Any variable that was ever in the denominator has a restriction).
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
(Even though 'b' cancels, you still have to state the restriction on it. (Any variable that was ever in the denominator has a restriction).
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Multiply by the reciprocal, simplify the coefficients, and reduce the variables,
n ≠ 0, m ≠ 0
You state a restriction on 'm' even if it is on the top? → Yes, would have become if we took the time to write it and you can see the variable 'm' is in the denominator so the restriction has to be stated.
You state a restriction on 'm' even if it is on the top? → Yes, would have become if we took the time to write it and you can see the variable 'm' is in the denominator so the restriction has to be stated.
Solution
Rational Expressions with Multiplication and Division of Monomials with Negative Exponents
Simplify and state the restrictions.
Solution
a ≠ 0, b ≠ 0
Solution
a ≠ 0, b ≠ 0
Solution
x ≠ 0, y ≠ 0
Solution
Video
x ≠ 0, y ≠ 0
Rational Expression Simplification
The following is simplified fully.
Solution
The top has two terms (separated by + or -), so you should to distribute, the collect like terms, then factor...
(restrictions: x ≠ 1, -5)
Rational Expressions: Restrictions
State the restrictions for the following rational expressions:
Solution
Solution
Solution
Solution
Video
(Don't forget to state a restriction on anything that was ever a denominator, so even though the 7x-1 gets flipped to the top, it still has to be included in the restriction list!)
(Don't forget to state a restriction on anything that was ever a denominator, so even though the 7x-1 gets flipped to the top, it still has to be included in the restriction list!)
Rational Expressions with Multiplication and Division
Simplify (Optional: state the restrictions)
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Solution
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Factor stuff first... Then cancel across the top & bottom...
Restrictions: x ≠ -4, +4, 0, -2, +3
Solution
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Change the denominator to make it the same as one binomial in the numerator.
Restriction: x ≠ -3
Quadratic Functions
Transformations and Translations of Functions with y = af[k(x - d)] + c
Determine the transformations and translations in the following functions, and any asymptotes (if exists).
y = 2(x - 2)2 + 1 Solution
y = 7(2(x - 3))2 - 3 Solution
y = -2(3x + 6)2 + 0 Solution
Solution
- Vertical reflection (on the x-axis)
- Horizontal shift 4 units left
- Vertical shift 2 units down
- Vertical reflection (on the x-axis)
- Horizontal shift 4 units left
- Vertical shift 2 units down
Solution
Transformation: Vertical stretch by 2
Transformation: k = 4, Horizontal stretch (compression) by factor of 1/k = 1/4
Translation: 3/4 units left
Translation: 5 units down
Transformation: Vertical stretch by 2
Transformation: k = 4, Horizontal stretch (compression) by factor of 1/k = 1/4
Translation: 3/4 units left
Translation: 5 units down
Solution
Vertical stretch by a factor of 3/2
Translation 7 units up
Translation 1/2 units left
Asymptotes at y = 7, and x = -1/2
Vertical stretch by a factor of 3/2
Translation 7 units up
Translation 1/2 units left
Asymptotes at y = 7, and x = -1/2
Solution
Asymptotes at y = 0, and x = -1, +2
Solution
Asymptotes at y = 0, and x = -1/2, - 4
Solution
Asymptotes at y = 0, and x = -1, -2
Solution
- Vertical stretch by a factor of 3
- Horizontal reflection (on y-axis)
- Horizontal stretch by a factor of 4 (it's because 1/k...)
- Horizontal shift 8 units left
- Vertical shift 3 units up
- Vertical stretch by a factor of 3
- Horizontal reflection (on y-axis)
- Horizontal stretch by a factor of 4 (it's because 1/k...)
- Horizontal shift 8 units left
- Vertical shift 3 units up
Solution
Transformations and Translations of Individual Coordinates with Function Notation y = aƒ[k(x - d)] + c
Determine the new coordinate (image) given function notation and a point:
ƒ(x - 3), P(1, 2)
Solution
Hint
Clear
Info
( , )
Incorrect Attempts:
CHECK
Hint Unavailable
Horizontal shift 3 units right...
Only affects the x-value
(1 + 3, 2)
= (4, 2)
Only affects the x-value (1 + 3, 2)
= (4, 2)
ƒ(x) - 3, P(5, -2)
Solution
Hint
Clear
Info
( , )
Incorrect Attempts:
CHECK
Hint Unavailable
This is a vertical shift 3 units down...
Only affects the y-value
(5, -2 - 3)
= (5, -5)
Only affects the y-value (5, -2 - 3)
= (5, -5)
2ƒ(x), P(-3, 4)
Solution
Hint
Clear
Info
( , )
Incorrect Attempts:
CHECK
Hint Unavailable
Vertical stretch by a factor of 2...
This affects the y-value because it's vertical.
(-3, 4 × 2)
= (-3, 8)
This affects the y-value because it's vertical. (-3, 4 × 2)
= (-3, 8)
ƒ(0.5x), P(2, -7)
Solution
Hint
Clear
Info
( , )
Incorrect Attempts:
CHECK
Hint Unavailable
Horizontal transformations by a factor of 1/k !
This is a horizontal stretch by factor of 2
This affects the x-value
(2 × 2, -7)
= (4, -7)
This is a horizontal stretch by factor of 2
This affects the x-value (2 × 2, -7)
= (4, -7)
ƒ(3x), P(1, 2)
Solution
Hint
Clear
Info
( , )
Incorrect Attempts:
CHECK
Hint Unavailable
Horizontal transformations by a factor of 1/k !
This is a horizontal compression by a factor of 1/3
On the x-value
(1 × ⅓, 2)
= (0.33, 2)
This is a horizontal compression by a factor of 1/3
On the x-value (1 × ⅓, 2)
= (0.33, 2)
ƒ(2x - 6) - 3, P(1, -4)
Solution
Hint
Clear
Info
( , )
Incorrect Attempts:
CHECK
Hint Unavailable
Careful!
To get the horizontal shift you have to factor out the horizontal stretch/compression first!
This is a horizontal compression by 1/2
Horizontal shift by 3 units right
Vertical shift 3 units down
(1 × ½ + 3, -4 - 3)
= (3.5, -7)
To get the horizontal shift you have to factor out the horizontal stretch/compression first! This is a horizontal compression by 1/2
Horizontal shift by 3 units right
Vertical shift 3 units down (1 × ½ + 3, -4 - 3)
= (3.5, -7)
-2ƒ(¼x + 1)2 - 5, P(2, 3)
Solution
Hint
Clear
Info
( , )
Incorrect Attempts:
CHECK
Hint Unavailable
Transformations to 'y'...
- Vertical reflection
- Vertical shift by a factor of 2
- Vertical shift 5 units down
Transformations to 'x'...
- Horizontal stretch by a factor of 4
- Horizontal shift 4 units left
Apply the transformations to 'x' on the 'x' value, and the transformations to 'y' to the 'y' value...
- Vertical reflection
- Vertical shift by a factor of 2
- Vertical shift 5 units down
- Horizontal stretch by a factor of 4
- Horizontal shift 4 units left
Domain and Range: Root Function
State the domain and range of the function:
Solution
Hint
Clear
Info
x∈ℝ, x ≥ ━━
y∈ℝ, y ≤
Incorrect Attempts:
CHECK
Hint Unavailable
y∈ℝ, y ≤
Quadratic Functions Comparing the Discriminant to Zero
For what values of k will the following functions have no zeros, one zero, and two zeros?
ƒ(x) = 4x2 - 2x + k
Solution
Video
k =
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
for 1 x-intercept...
for 2 x-intercepts...
for 0 x-intercept...
ƒ(x) = kx2 + x + k
Solution
Video
k =
Hint
Clear
Info
± ━━
Incorrect Attempts:
CHECK
Hint Unavailable
Determining the Equation of a Parabola Given Roots and a Point
Determine the equation of the parabola in factored form given the following information. The x-intercepts of the function are x = 7, -1, and a point on the curve is P(2, 30).
Solution
ƒ(x) =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(7, 0) and (-1, 0) and (2, 30)...
So the equation is,
Determining the Equation of a Parabola Given an Incomplete Equation and a Point
Determine the complete standard form equation of the function ƒ(x) = nx2 - 2x when ƒ(3) = 12.
Solution
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Incorrect Attempts:
CHECK
Hint Unavailable
So the equation in standard form is,
⁰
¹
²
³
⁴
⁵
⁶
⁷
⁸
⁹
⁻
⁺
⁽
⁾
₀
₁
₂
₃
₄
₅
₆
₇
₈
₉
₋
₊
₍
₎
Solve for Various Aspects of a Quadratic Function
When a soccer ball is kicked the parabolic path of its vertical height, h, in meters is given by the equation below, where the time, t, is in seconds.
Determine the height of the ball the moment it was kicked.
Solution
h =
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
at t = 0, height = 0.1 m
Determine the maximum height reached by the soccer ball and the time it takes to reach this maximum height.
Solution
Hint
Clear
Info
Height:
m
Time:
s
Incorrect Attempts:
CHECK
Hint Unavailable
The maximum height occurs at the vertex (not shown)...
11.35m at 1.5s
11.35m at 1.5s
How long will it take the soccer ball to hit the ground?
Solution
t =
Hint
Clear
Info
Incorrect Attempts:
CHECK
s
Hint Unavailable
3.0 s (when height = 0)
At what time(s) will the ball be at a height of 6.0m
Solution
Hint
Clear
Info
t1:
t2:
Incorrect Attempts:
CHECK
s
Hint Unavailable
0.47 s, and 2.53 s
Determining the Minimum of a Quadratic Function
When a special spring gets pulled by a certain amount in meters, x, the plastic feels a force, f, in newtons. Determine the exact value of the minimum force on the spring.
Solution
F =
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
N
Hint Unavailable
The minimum occurs at the vertex... (complete the square shown here)
The minimum force is N.
Point of Intersection Between a Quadratic and Linear Function
Determine the point(s) of intersection of the functions below. Round your answers to one decimal place where necessary.
Solution
Video
Hint
Clear
Info
(-1, ) & ( , )
Incorrect Attempts:
CHECK
Hint Unavailable
Solve the system using substitution. Substitute for y...
a = 5, b = -24, c = -30...
Solve by completing the square or using the quadratic (shown here)...
Find y by substitution into any equation...
(-1, 5.6) & (5.8, 1.5)
Solve by completing the square or using the quadratic (shown here)... Find y by substitution into any equation... (-1, 5.6) & (5.8, 1.5)
Quadratic Word Problems
Solve the following word problems using quadratics.
[Type: Integers] Find any three consecutive odd integers such that the sum of the squares of the first two is 15 less than the square of the third.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
[Type: Integers II] Find two complex numbers with a sum of 4 and a product of 13. (Skip this question if you haven't yet learned Complex Numbers.)
Solution
Video
Hint
Clear
Info
±
Incorrect Attempts:
CHECK
Hint Unavailable
[Type: Geometry] Jackie mows a strip of grass with a uniform width around her 25 m by 15 m rectangular lawn and leaves a patch of lawn that is 20% of the original area. What is the width of the strip?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
Set up an equation comparing the original and the new areas...
Therefore x = 5m, and 15m.
But since one side is 15 m, it is impossible for the width of the uniform strip to be 15m, because this would be at least 30 m...
Therefore the width of the strip must be 5 m.
But since one side is 15 m, it is impossible for the width of the uniform strip to be 15m, because this would be at least 30 m...
Therefore the width of the strip must be 5 m.
[Type: Geometry II] An 11 x 18 cm photograph is being mounted so that the matte board provides a border around the photograph that has an uniform width on all sides. Determine the dimensions of the matte board so that the area of the boarder is equal to the area of the photograph.
Solution
Hint
Clear
Info
Larger: Smaller:
Incorrect Attempts:
CHECK
cm
Hint Unavailable
[Type: Money] Determine the break even point given the cost function c(x) = x + 100 and the revenue function r(x) = -2x2 + 42x + 200, where x is the number of items sold.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
items
Profit = Revenue - Cost
- This particular setup has # sold on the x-axis, and amount of money on the y-axis
- The break even point is the first positive point of intersection (POI) between the cost and the revenue function...
Find the POI by solving the system of equations with substitution...
Solve using the quadratic equation, where a = 2, b = -41, and c = -100...
Therefore rounding the number of items sold up to the nearest whole number, the break even point is when 23 items are sold.
- This particular setup has # sold on the x-axis, and amount of money on the y-axis
- The break even point is the first positive point of intersection (POI) between the cost and the revenue function...
[Type: Money] A bus company has 4000 passengers daily, each paying a fare of $2.00. For each $0.15 increase, the company estimates that it will lose 40 passengers per day. If the company needs to take in $10,450.00 per day to stay in business, then what fare must be charged?
Solution
 $
Hint
Clear
Info
Incorrect Attempts:
CHECK
Revenue = (Price)(Number Sold)
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Revenue = (Price)(Number Sold)
[Type: Distance, Speed, Time] A person drives a car 100km on the highway to point 'A'. Then they travel the same distance, 100km in the same direction to point 'B'. If the person travels 11 km/hr faster to point 'B', and the total time is 1.9 hours, determine the speed of the car to point 'A'.
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
km/hr
Make a table containing the distance, speed, and time for each of the two trips. Remember that distance = (speed)(time)
Set up a table to organize the values: distance, speed, and time.
to point A to point B
Distance (km) 100 100
Speed (km/hr) s s + 11
Time (hr)
The total time is 1.9 hours...
Get rid of the denominator by multiplying all 3 terms by (s)(s + 11)
Use the quadratic equation to solve
Since the speed is positive it must be...
| to point A | to point B | |
| Distance (km) | 100 | 100 |
| Speed (km/hr) | s | s + 11 |
| Time (hr) |
Finding the Vertex
List the 3 different ways to find a maximum or minimum. Record these in your notes. Solution
Complex Numbers and the Imaginary Unit i where
Simplify
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Adding, Subtracting, Multiplying, and Dividing Complex Numbers
Expand and simplify.
(4 + 3i) - (-3 + 2i)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
2(3i2)3
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
(4 + 3i)(4 - 3i)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
2(-4 + 2i)2
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Remove the imaginary number, 'i' from the denominator this way:
Trigonometry
Right Triangles (Grade 10 Review)
Solve for the variable:
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Right Triangles (Grade 10 Review)
The side length, y is calculated by which of the following?
Solution

y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
Right Triangles (Grade 10 Review)
Angle A is calculated by which of the following?
Solution

A =
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Acute and Obtuse Triangles (Grade 10 Review)
The following acute triangle, ABC contains the known values (SSA) indicated on the diagram below.

What would be used to calculate angle C?
Solution
The Sin Law, as mentioned previously.
Which of the following measures can be calculated first with the information given in the diagram of an acute triangle?
Solution
When the triangle is not a right angle (90˚) triangle, you can't use SOH CAH TOA.
Therefore we must use: Sine Law or Cosine Law.
In this case, since we have the pair angle A (40˚) and side 'a' (6cm), and the side 'c', then using the Sin Law, angle C can be calculated first.
Therefore we must use: Sine Law or Cosine Law. In this case, since we have the pair angle A (40˚) and side 'a' (6cm), and the side 'c', then using the Sin Law, angle C can be calculated first.
How would angle C be calculated in the acute triangle?
Solution
C =
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
The Sine Law
Acute and Obtuse Triangles (Grade 10 Review)
Calculate the missing side length in the following diagram of an acute triangle.
Solution
 b =
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
The Cosine Law
b =
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
The Cosine Law
Acute and Obtuse Triangles (Grade 10 Review)
Find angle A indicated in the following diagram of an acute triangle.
Solution
 A =
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
The Cosine Law
A =
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
The Cosine Law
Acute and Obtuse Triangles (Grade 10 Review)
Sydney is at home and needs to quickly pick up some things from the grocery store to make a special dinner for her friends. There are two stores she could go to, store 'A' and store 'B' are 10km apart and make an angle of 40˚ from Sydney's house to the stores. Store 'A' makes an angle of 75˚ between store 'B' and Sydney's home.
Find the angle store 'B' makes with store 'A' and Sydney's home.
Solution
B =
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Sum of a Triangle = 180˚
(Sketch not shown)
Calculate which store is closer to Sydney's home, store a or b? [1]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Sine Law:
Therefore store 'A' is closer.
(Careful! side b is opposite the angle of store 'B', and is really the distance to store 'A')
(Careful! side b is opposite the angle of store 'B', and is really the distance to store 'A')
Sine Law and Cosine Law (Grade 10 Review)
Both the Sine Law and the Cosine Law can be used in right angle triangles.
Solution
Sine and Cosine Laws are typically used for acute and obtuse triangles, but they also work for right angle triangles. Typically SOH CAH TOA is used for right angle triangles, instead of Sine Law and Cosine Law.
Sine Law and Cosine Law (Grade 10 Review)
Given the adjacent side lengths, angle-angle-side (AAS) in an acute triangle which of the following will solve the triangle?
Solution
Use Sine Law for AAS or SSA
Given adjacent side lengths, side-side-angle (SSA) in an acute triangle, which of the following will solve the triangle?
Solution
Use Sine Law for AAS or SSA
Given adjacent side lengths, side-angle-side (SAS) in an acute triangle, which of the following will solve the triangle?
Solution
Use Cosine Law for SSS or SAS
Equivalencies
Determine if the following is true or false.
Solution
You will learn the explanation later in this unit. For now you can use your calculator to evaluate and see the equivalence.
Angles
Which of the following is the correct solution to:
Solution
To solve for the angle theta, take the inverse sine of the ratio on the right-hand side of the equal sign.
The Location of Angles in the Quadrant System
Determine the location of each angle.
Which of the following angles is in quadrant 1?
Solution
The negative angle -300˚ starts from 0˚ and rotates clockwise to the first quadrant.
θ = 120˚
Solution
Start from 0˚ on the x-axis and rotate counter-clockwise, past 90˚ to 120˚ in quadrant 2, before 180˚.
θ = -135˚
Solution
Start from 0˚ and rotate in the negative direction, clockwise by 135˚. This puts the terminal arm in Quadrant 3 in the normal sense.
θ = 420˚ = 60˚ + 360˚
Solution
420˚ is a coterminal angle (greater than 360˚).
= 420˚
= 60˚ + 360˚
≈ 60˚
This is located in quadrant 1
= 420˚
= 60˚ + 360˚
≈ 60˚
This is located in quadrant 1
θ = 700˚
Solution
700˚ is a coterminal angle.
= 340˚ + 360˚
≈ 340˚
This is in Quadrant 4.
= 340˚ + 360˚
≈ 340˚
This is in Quadrant 4.
Signs of Trig
Sin is positive in which of the following quadrants?
Solution
Use C.A.S.T. Sin is positive in 'A' and 'S', which corresponds to Quadrant 1 and Quadrant 2.
Predict which of the following will be negative.
Solution
Using your understanding of a graph of cos180˚ or using your calculator, you can see the value of this is -1.
If tan is negative, then the terminal arm (ray) can only be located in Quadrant 2.
Solution
Tan is negative in quadrant 2 and quadrant 4.
Trig and Points on Terminal Arms
Given that a point on the terminal arm makes a right angle triangle with the reflex angle...
A point on the terminal arm in quadrant 2, using the ratio below, could be (-1, 1).
Solution
The point (-1, 1) gives the side lengths (x, y) of the triangle formed with the reflex angle.
Opposite = y = 1
Adjacent = x = -1
Point: (-1, 1)
Adjacent = x = -1
Point: (-1, 1)
A point on the terminal arm in quadrant 4, using the ratio below, could be (1, -1).
Solution
Opposite = y = -1
Find the hypotenuse using the Pythagorean Theorem:
Point =
Find the hypotenuse using the Pythagorean Theorem:
Point =
Trig and Points on Terminal Arms
The point (-2, 1) is on the terminal arm of an angle in standard position. Find the value of Sin and the related acute angle, in degrees.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Need to determine the length of the hypotenuse using pythagorean theorem first. Then use a trig ratio...
x = -2, y = 1
Need to determine the length of the hypotenuse using pythagorean theorem.
Opposite = 1, Hypotenuse =
Trig and Points on Terminal Arms in Unit Circle
In a unit circle, the terminal arm always has a radial length of 1 unit.
Solution
'radius' is interchangeable with 'hypotenuse' here.
For an angle in standard position, determine a point (coordinate) on the terminal arm given the value sin60˚.
Solution
Video
sin60˚ is a "30 - 60 - 90" special triangle with: x = 1, y = , and hypotenuse = 2
In a unit circle, the terminal arm always has a radial length (hypotenuse) of 1 unit. So, need to convert hypotenuse of 2.0 to 1.0 by dividing all points by 2.
So the point on the terminal arm (x, y) is .
In a unit circle, the terminal arm always has a radial length (hypotenuse) of 1 unit. So, need to convert hypotenuse of 2.0 to 1.0 by dividing all points by 2. So the point on the terminal arm (x, y) is .
Determine a point on the terminal arm for
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
gives a 45-45-90 special triangle where x = 1, y = 1, hypotenuse =
In a unit circle, the terminal arm always has a radial length (hypotenuse) of 1 unit. So, need to convert hypotenuse = to 1 by dividing all points by .
So the point on the terminal arm (x, y) is .
In a unit circle, the terminal arm always has a radial length (hypotenuse) of 1 unit. So, need to convert hypotenuse = to 1 by dividing all points by . So the point on the terminal arm (x, y) is .
The Reference Angle
The related acute angle is also known as the reference angle.
Solution
This is the angle that is formed between the terminal arm and the nearest x-axis.
Which of the following would have a 60˚ reference angle?
Solution
The reference angle is formed from the terminal arm to the nearest x-axis. 120˚ is in Quadrant 2 and has a related acute angle of 60˚ with the nearest x-axis.
Determine the principle angle that would have a 60˚ reference angle in quadrant 3, on the interval 0 ≤ x ≤ 360˚.
Solution
sin
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
The reference angle is formed from the terminal arm to the nearest x-axis. The principle angle, 240˚ is in Quadrant 3 and has a related acute reference angle of 60˚ with the nearest x-axis.
Special Triangles
Fill in the blank of the special triangle sides. Solution
| Triangle 1 | 1 | 2 | |
| Triangle 2 | 1 | __ |
Exact Values
Determine the exact value of cos30˚ in quadrant 1.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use 30-60-90 special triangle
Use 30-60-90 special triangle to find:
Determine the exact value of cos45˚ in quadrant 1
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use 45-45-90 special triangle...
Use 45-45-90 special triangle to find:
Must de-rationalize the denominator!
Must de-rationalize the denominator!
Exact Values
Determine the exact value of each of the following:
cos30˚
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Reference angle = 30˚ in quadrant 1
Use special triangle side lengths:
Use special triangle side lengths:
sin135˚
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use 45-45-90 special triangle...
Reference angle = 45˚ in quadrant 2
Use special triangle side lengths:
Use special triangle side lengths:
tan660˚
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Coterminal angle with 660˚ - 360˚ = 300˚
Reference angle = 60˚ in quadrant 4
Use special triangle side lengths:
Reference angle = 60˚ in quadrant 4
Use special triangle side lengths:
cos(-120˚)
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Reference angle = 60˚ in quadrant 3
Use special triangle side lengths:
Use special triangle side lengths:
Exact Values
Determine the exact value of the following, without the use of a calculator. Simplify fully.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Use 45-45-90 special triangle...
Reference angle = 45˚ in quadrant 3
Reference angle = -420˚ + 360˚ = -60˚ = 60˚ in quadrant 4
Use special triangle side lengths:
Reference angle = -420˚ + 360˚ = -60˚ = 60˚ in quadrant 4
Use special triangle side lengths:
Radian Measure
Which of the following is the correct definition of 1 radian.
Solution
Radian Measure
radians equals
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Converting Degrees and Radians
Convert the following angles into radians.
60˚
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
radians
Hint Unavailable
120˚
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
radians
Hint Unavailable
180˚
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
radians
Hint Unavailable
270˚
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
radians
Hint Unavailable
Converting Degrees and Radians
Convert the following angles into degrees.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
2.1 radians
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Radian Measure Applications
A 5.5 radian angle sweeps out (subtends) a 20 cm arc length. Calculate the radius.
Solution
Video
r =
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
angle = 5.5 radians
Calculate the angle, in radians if the arc length is 75% (¾) of a full circle with a radius of 10 cm. (Remember the circumference of a circle = )
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
radians
Hint Unavailable
Determine the area of the sector of a circle with radius 18 cm, if the sector is subtended by an angle of 105˚.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm2
Hint Unavailable
If in radians
If in degrees
Given r = 18cm and θ = 105˚, solve...
A person's visual field sweeps out 160˚ in-front of them. If the curvature of the Earth prevents a person from seeing further than 5 km on flat ground on a clear day, then calculate the arc length of a person's visual acuity.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
km
Hint Unavailable
Convert 160˚ to radians
Calculate the arc length (perimeter)...
Trig Identities
Which of the following is incorrect?
Solution
"soc" is not a trig ratio.
Exact Values with Radians
Determine the exact value (y-value) of each of the following, given the angles. (A calculator will not work for this. Hint: draw a sketch of the principle angle first).
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Draw a sketch with is the principal angle in Quadrant 2.
REFERENCE ANGLE:
Draw a sketch of the reference angle in quadrant 2 to determine the following:
x = -1, y = , r = 2
REFERENCE ANGLE: Draw a sketch of the reference angle in quadrant 2 to determine the following:
x = -1, y = , r = 2
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Exact Values with Radians
Determine the exact value of the following. Note that we can use a calculator to find the exact value only when the angles are a multiple of .
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Determining Radian Angles Given Exact Values
Using the CAST system, determine two angles between 0 and that have the following values:
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
radians
Hint Unavailable
CAST: tan is negative in Quadrants 2 and 4.
Based on the side lengths, -1 and 1, or 1 and -1:
Reference angle = 45˚
The angles () in your answer will be the two principle angles:
Quadrant 2 = 180˚ - 45˚ = 135˚
Quadrant 4 = 360˚ - 45˚ = 315˚
Based on the side lengths, -1 and 1, or 1 and -1:
Reference angle = 45˚
The angles () in your answer will be the two principle angles:
Quadrant 2 = 180˚ - 45˚ = 135˚
Quadrant 4 = 360˚ - 45˚ = 315˚
Hint
Clear
Info
Incorrect Attempts:
CHECK
radians
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
radians
Hint Unavailable
Hint
Clear
Info
Incorrect Attempts:
CHECK
radians
Hint Unavailable
Trig Ratios and Terminal Arm Coordinates on Intervals
Determine all angles on the interval , the exact values of and , and the exact value of the coordinate on the terminal arm.
Solution
Video
coordinate =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Make a sketch using CAST... The negative cosine on the interval can only exist in quadrant 2. Make the special triangle with the reflex angle with the x-axis...
Determine the exact values from your sketch of the special triangle with an acute angle of ...
The terminal arm must have a length (hypotenuse) of 1, therefore the coordinates must be...
Solving Trig Equations
The following operations are correct.
Solution
Notice this is a difference of squares with a trig function in place of x2.
E.g) 0 = x2 - 1 = (x + 1)(x - 1)
x = -1, +1
E.g) 0 = x2 - 1 = (x + 1)(x - 1)
x = -1, +1
Solving Trig Equations
Solve the following between: . Order your answers from lowest to highest.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
radians
Hint Unavailable
CAST: tan is negative in Quadrants 2 and 4.
For determine that the REFERENCE ANGLE = 45˚ or and then find the principle angles on the CAST plane:
For determine that the REFERENCE ANGLE = 30˚ or and then find the principle angles on the CAST plane:
Hint
Clear
Info
Incorrect Attempts:
CHECK
radians
Hint Unavailable
For determine that the REFERENCE ANGLE = 30˚ or and then find the principle angles on the CAST plane:
For determine that the REFERENCE ANGLE = 45˚ or and then find the principle angles on the CAST plane:
Solving Trig Equations
Given the trig equation,
How many answers will the following equation have, between the interval: ?
Solution
This resembles 4x2 - 4x + 1 = 0
Factor:
Cos is positive in quadrant I and IV... there are 2 answers.
Factor: Cos is positive in quadrant I and IV... there are 2 answers.
Solve for the principle angles, in degrees.
Solution
Hint
Clear
Info
= =
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Solve for θ:
Cos is positive in quadrant I and IV... Principle angles with 60˚ reflex angles are: 60˚, 300˚.
Solving for the Angle
Solve for x, in degrees.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
Necessary Trig Shortcuts
Side length 'a' can be written as:
Solution
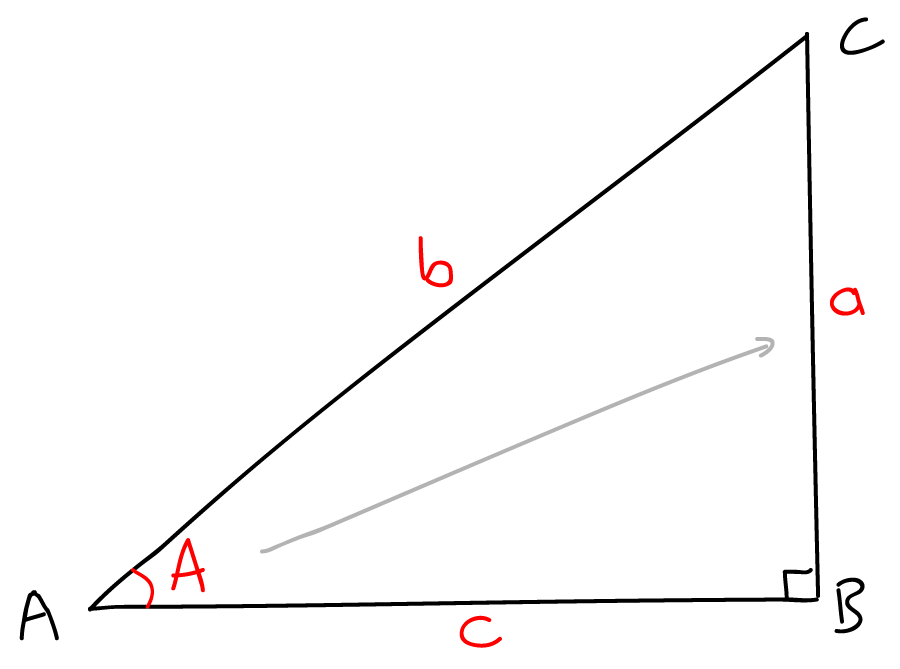
Side length 'a':
Side length 'c':
Determine side length AB.
Solution
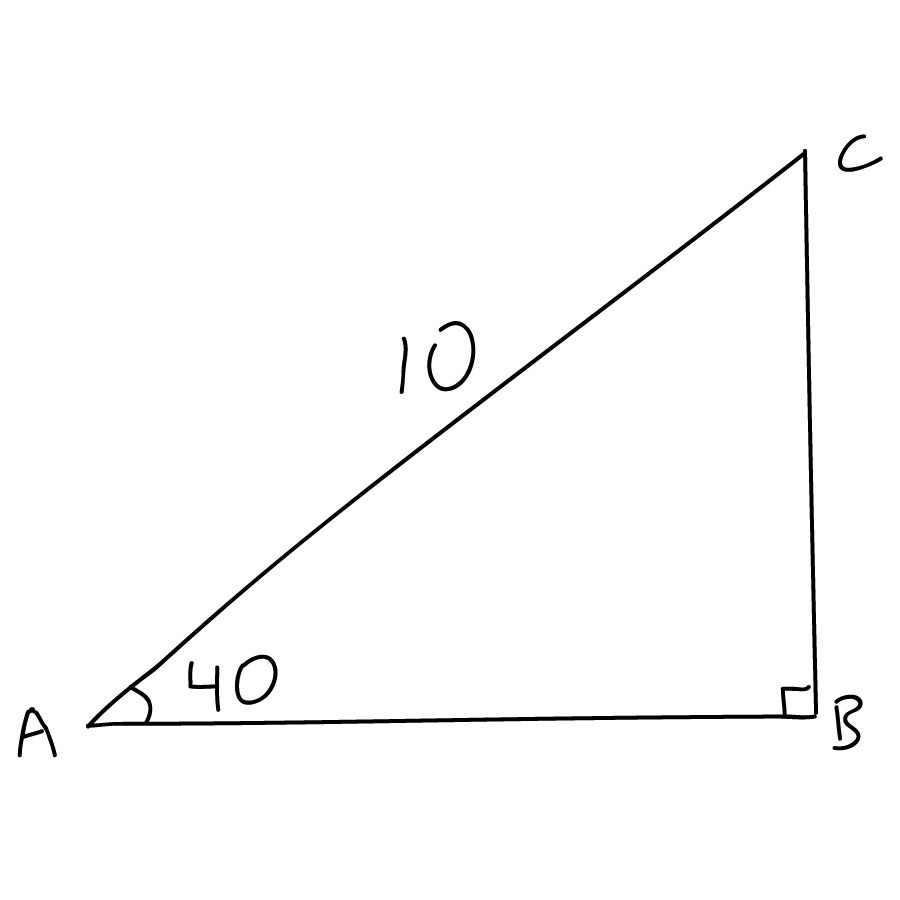
Side length AB:
The Ambiguous Case
When the height of a right triangle is equal to one of the side lengths, there are 2 possible triangles.
Solution
When the height of a right triangle is equal to one of the side lengths, there is only 1 possible triangle.
The Ambiguous Case
Triangle XYZ has side length XY = 4m and angle Y = 48.6˚. Determine the side length XZ that gives one solution.
Solution
One solution when height = XZ.
Since height = 3m, then side length XZ would be 3m for a triangle with one solution.
The Ambiguous Case
Triangle ABC has side length AB = 5cm, angle B = 40˚, and side length AC = 4cm.
Determine the height of triangle ABC.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
How many triangles are possible?
Solution
Compare the height of triangle ABC to side length AC.
Since height < AC, then there are 2 possible triangles: one acute, and one obtuse.
Since height < AC, then there are 2 possible triangles: one acute, and one obtuse.
The Ambiguous Case
Triangle LMN has side length LM = 40cm, angle M = 15˚, and side length LN = 10cm. How many triangles are possible?
Solution
Find the height of triangle LMN and compare to side length LN.
Since height > LN, then there are no possible triangles.
Tan Graph
A graph of tanx has vertical asymptotes because
Solution
Since cosx ≠ 0, then a vertical asymptote occurs wherever cosx = 0.
Trig Identities
Which of the following is not a trig identity?
Solution
... is not a trig identity.
Periodic Trig Functions
Terms of Periodic Functions
Period, in the context of trigonometric functions, is...
Solution
In other words, period (T) is the time for one complete cycle. A cycle is for example a rotation, or a revolution, or really any complete unit of an oscillating system.
Period and frequency have reciprocal relationships, shown below.
Solution
Frequency is calculated as the number of cycles divided by the total time for those cycles, for example,
Properties of Periodic Functions
For the graphs of the parent functions of and :

The range for the graphs is the same:
Solution
True. The range for both of the functions is between a maximum y-value of +1, and a minimum y-value of -1. Hence,
The phase shift, or horizontal translation between the graphs of these functions is by how many units?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
radians
Hint Unavailable


Properties of Periodic Functions
Consider a graph of the parent function between the interval:
The maximums (peaks, or crests) are located at:
Solution


The x-intercepts are located at:
Solution


Transformations of Periodic Functions with Function Notation:
State the transformation on each of the following:
Solution
The 'b' value must be factored out of the brackets first!
Therefore the phase shift is 30˚ right
Therefore the phase shift is 30˚ right
Transformations of Periodic Functions:
State the transformations on the function:
Solution
Hint
Clear
Info
· Horizontal translation units
· Vertical stretch by a factor of
· Vertical translation units
Incorrect Attempts:
CHECK
Hint Unavailable
Horizontal translation units left
Vertical stretch by a factor of 5
Vertical translation units up
· Vertical stretch by a factor of
· Vertical translation units
Vertical stretch by a factor of 5
Vertical translation units up
Characteristics of Graphs of Trig Parent Functions
Which of the following is not a similarity between the functions ƒ(x) = sinθ and ƒ(x) = cosθ?
Furthermore the following features are also similar: amplitude, range. The only differences are the x-intercepts and y-intercepts.
Graphing Key Points of Trig Functions
Given the trig function below:
ƒ(x) = -4cos 2(θ + ) - 4Determine the coordinate according to the given function.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
In other words, given x = , determine
The coordinate:
The coordinate:
Determine the image of the key point after it is transformed according to the given function.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Starting with x = , y = 0
The transformed points are in the form below (x2, y2):
a = -4
b = 2
c =
d = -4
The point (x2, y2) is:
The transformed points are in the form below (x2, y2):
a = -4
b = 2
c =
d = -4
The point (x2, y2) is:
Characteristics of Graphs of Trig Parent Functions
How many times do the functions ƒ(x) = sinθ and ƒ(x) = cosθ cross the x-axis in the domain -360˚ ≤ θ ≤ 360˚, respectively?
Solution
Hint
Clear
Info
&
Incorrect Attempts:
CHECK
Hint Unavailable
How many times do the functions ƒ(x) = sinθ and ƒ(x) = cosθ cross 'eachother' in the domain -360˚ ≤ θ ≤ 360˚?
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Transformations of Trig Functions
Determine the range of the function,
Solution
Hint
Clear
Info
y∈ℝ, ≤ y ≤
Incorrect Attempts:
CHECK
Hint Unavailable
The amplitude is 2, and the axis of symmetry is shifted down to y = -2. So the maximum is y = 0, and the minimum is y = -4.
Features of Trig Functions
A minimum occurs on a periodic function at 3:00pm and again at 11:00pm.
Determine where the maximum occurs.
Solution
The maximum occurs in the middle between two minimums. So between 3pm and 11pm is 7pm.
At what time would the function be located at the axis of symmetry?
Solution
Halfway between a minimum (3:00pm) and a maximum (7:00pm).
= 5:00pm
= 5:00pm
Features of Trig Functions
Determine the features below given the function:
The amplitude
Solution
a =
Hint
Clear
Info
Incorrect Attempts:
CHECK
ƒ(x) = a·sin(x - d) + c
ƒ(x) = a·sin(x - d) + c
a = 4
a = 4
The vertical translation
Solution
c =
Hint
Clear
Info
Incorrect Attempts:
CHECK
units
ƒ(x) = a·sin(x - d) + c
ƒ(x) = a·sin(x - d) + c
c = 10 units up
c = 10 units up
The horizontal translation
Solution
ƒ(x) = a·sin(x - d) + c
d = radians right.
d = radians right.
The period
Solution
period =
Hint
Clear
Info
Incorrect Attempts:
CHECK
rads
Hint Unavailable
ƒ(x) = a·sin[b(x - d)] + c
b = 1
Period =
Period =
b = 1
Period =
Period =
The equation of the axis of symmetry.
Solution
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
'c' is the axis of symmetry.
ƒ(x) = a·sin(x - d) + c
y = 10
ƒ(x) = a·sin(x - d) + c
y = 10
The y-value at the y-intercept.
Solution
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The y-intercept occurs when x = 0
(0, 10)... y = 10
The maximum y value.
Solution
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The maximum value occurs at |a| + c
ƒ(x) = a·sin(x - d) + c
y = 14
ƒ(x) = a·sin(x - d) + c
y = 14
Introduction to Period (T) on a Periodic Function
The period in the function below is 5
Solution
ƒ(x) = a·cos[k(x - d)] + c
The 'k' value in the equation is 5, so k = 5
Note that you need to use the following equation to convert 'k' to period, T:
The 'k' value in the equation is 5, so k = 5
Note that you need to use the following equation to convert 'k' to period, T:
Period of a Periodic Function
A periodic function expresses the period as a horizontal stretch or compression, with the value k according to the formula:
The period of the function below is:
Solution
 Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
See that this function repeats itself over 720˚ intervals...
Hint
Clear
Info
Incorrect Attempts:
CHECK
degrees
Hint Unavailable
See that this function repeats itself over 720˚ intervals...
Determine the exact value of the k-value in the following...
Solution
 k =
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
The period is one full cycle.
k =
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
The period is one full cycle.
Period =
Period =
Determine the exact value of the k-value in the following...
Solution
 k =
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Half of a period is from to , so the full period equals .
k =
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Half of a period is from to , so the full period equals .
Transformations on a Periodic Function, Including Period
Determine the equation of the function of cos(x) given the transformations in the table below. Solution
| Transformation | Value |
| Amplitude | |
| Phase Shift | units right |
| Vertical Shift | 4 units down |
| Period |
T =
So we need to calculate 'k' using 'T' with the equation below, and sub 'k' in: The general form of an equation is:
Transformations on a Periodic Function, Including Period
Determine the equation of the sin(x) function given the adjacent maximum and minimum points in the table below. Solution
| Aspect | Coordinate |
| y-intercept: | (0, 0) |
| Maximum: | |
| Minimum: |
The maximum and minimum are 1/2 cycle apart on the x-axis. The difference is 1/2 cycle: . Therefore 1 full cycle (Period, T) = .
So putting this altogether, the equation is:
Isolating the Independent Variable in the argument of a Trig Function
The following is correct.
Solve for the smallest value of 'x', with or without the use of a calculator.
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
˚
Hint Unavailable
Determine the smallest value of x in the following (with your calculator in degrees).
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
˚
Hint Unavailable
Isolate for x
Period and Amplitude
A buoy floating in the ocean bobs from its highest point to its lowest point in 0.5 seconds. The vertical displacement between the highest and lowest part of the buoy's motion is 60 cm.
Determine the period of the motion of the buoy in the ocean.
Solution
period =
Hint
Clear
Info
Incorrect Attempts:
CHECK
seconds
Hint Unavailable
If the buoy takes 0.5 seconds to transition from top to bottom (half a cycle), then the total period (T) for one full cycle is 1.0 seconds.
Determine the amplitude of the motion of the buoy in the ocean.
Solution
amplitude =
Hint
Clear
Info
Incorrect Attempts:
CHECK
cm
Hint Unavailable
The amplitude is the distance from a maximum or minimum to the equilibrium position.
This can be calculated by dividing the total displacement between max and min by 2.
So the amplitude is 60cm ÷ 2 = 30cm or 0.3m.
This can be calculated by dividing the total displacement between max and min by 2.
So the amplitude is 60cm ÷ 2 = 30cm or 0.3m.
Which of the following trigonometric functions could be used as a starting point to model the vertical motion of the buoy?
Solution
Depending on where you arbitrarily choose the origin point for time to start (t = 0), you can model this with either a sin or cos function. There are many possibilities...
For example one possibility is...
For example one possibility is...
Transformations on a Periodic Function, Word Problem
A bicycle wheel rotates once around every 1.0s, the center of the wheel is located 50cm above the ground. Determine an equation for the periodic function that models a rock stuck in the tire, starting at 100cm off the ground.
Solution
y =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
First, find the key properties:
Period, T = 1.0 s
Amplitude, A = 50cm
Principle axis (axis of symmetry), c = 50
Period, T = 1.0 s
Amplitude, A = 50cm
Principle axis (axis of symmetry), c = 50
Transformations on a Periodic Function, Word Problem
The average monthly maximum temperature of a certain city can be modeled by the periodic function below where T(t) is the temperature in ˚Celsius, and t is the time in months, where t = 0 represents January 1, t = 1 represents February 1, etc.

In what month of the year is the monthly maximum temperature the highest? [1]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
a = 7, c = 25
Plug this temperature into the function for T(t)...
This 6th month is in July 1st.
a = 7, c = 25
Plug this temperature into the function for T(t)... This 6th month is in July 1st.
Predict the monthly maximum temperature on June 1st (t = 5).
Solution
Tmax
Hint
Clear
Info
Incorrect Attempts:
CHECK
˚C
Hint Unavailable
t = 5
In what month of the year will the monthly maximum temperature first reach 20˚? [1]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
T(t) = 20˚ (Make sure everything is in radians because you have pi here).
If t = 0 represents January 1, t = 1 represents February 1, t = 2 represents March...
It will be some time in February.
It will be some time in February.
Transformations on a Periodic Function, Word Problem
A ferris wheel starts rotating from a point at ground level, represented by the equation below where H(t) is height above the ground, in meters, and t is time, in seconds.
 |
Determine the maximum height, in meters.
Solution
Video
H(t) =
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
Determine the period, in seconds.
Solution
Video
T =
Hint
Clear
Info
Incorrect Attempts:
CHECK
s
T = 2(pi)/k
Determine the radius of the ferris wheel.
Solution
Video
r =
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Think about what the amplitude represents
radius = amplitude
= 20m
= 20m
Transformations on a Periodic Function, Word Problem
A ferris wheel spins around a central axis, which is 15m above the ground. The diameter of the ferris wheel is 28m. The wheel spins once around in 1.0 minute. The rotation of the ferris wheel is plotted where function H(t) is the height of the axis above ground, in meters, and t is the time, in minutes.
 |
Determine the amplitude.
Solution
Video
a =
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Think about what the diameter and radius represent.
If the diameter is 28m, then the radius is 14m.
The amplitude is equal to the radius.
= 14m.
The amplitude is equal to the radius.
= 14m.
Determine the axis of symmetry.
Solution
Video
A.O.S. =
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Think about the height of the center of rotation, above the ground
How high is the axis above the ground?
If the diameter is 28m, then the radius is 14m.
The axis is 15m above the ground and the radius is 14m, so the bottom of the wheel is 1m off the ground.
The axis of symmetry is located at 1m + 14m = 15m.
(Note that the equation of the axis of symmetry would be y = 15.)
If the diameter is 28m, then the radius is 14m.
The axis is 15m above the ground and the radius is 14m, so the bottom of the wheel is 1m off the ground.
The axis of symmetry is located at 1m + 14m = 15m.
(Note that the equation of the axis of symmetry would be y = 15.)
Determine the maximum and minimum height of the wheel. [2]
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Axis of symmetry = 15m.
Amplitude = 14m.
Therefore a point on the wheel will alternate between a minimum height of 1m off the ground and a maximum height of 29m above the ground.
Amplitude = 14m. Therefore a point on the wheel will alternate between a minimum height of 1m off the ground and a maximum height of 29m above the ground.
Determine the equation of the function.
Solution
H(t) =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
First determine the value of 'k'
Lets say the point of rotation begins when H(t) is increasing, starting at the axis of symmetry, so d = 0
Put the amplitude (a), the axis of symmetry (c), and the value of k together:
Put the amplitude (a), the axis of symmetry (c), and the value of k together:
Determine the height of the wheel when t = 3.5 minutes.
Solution
H(t) =
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Solve for H(t) given t = 3.5 minutes...
Solve for H(t):
Determine a time (t) when the wheel is at the maximum height.
Solution
t =
Hint
Clear
Info
Incorrect Attempts:
CHECK
seconds
Hint Unavailable
Maximum height = H(t) = 29m.
Solve for (t):
Solve for (t):
Application of Revolutions (RPM) with Speed
The motor on a regular hobby-grade radio controlled (RC) car does 4,000 revolutions per minute (RPM). If someone replaces the stock 5cm diameter wheels with new 9cm diameter wheels. What is the increase in speed at maximum RPMs?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
m/s
Hint Unavailable
Know that 1 revolution is circumference of a circle is...
Find the speed (in m/s) with the first wheels...
For the second set of wheels with the new circumference...
The increase in speed is...
Quadratic Trig Functions
Determine the maximum and minimum values of the function. [2]
Solution
ƒ(x) = 5sin2x + 10sinx - 5
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Use a variable to determine the independent value of the minimum point.
let n = sinx
Then complete the square,
Therefore the minimum of the quadratic occurs when n = -1. Substitute 'n' back into the let statement, to get the point of inflection in degrees or radians...
This is a minimum, and then the nearest maximum occurs at 90˚, rad.
 Substitute this back into the original function to solve for the maximum and minimum values of the function...
Substitute this back into the original function to solve for the maximum and minimum values of the function...
 Substitute this back into the original function to solve for the maximum and minimum values of the function...
Substitute this back into the original function to solve for the maximum and minimum values of the function...
Exponential Functions
Exponent Law Help
Solution
Exponent Law Help
Which of the following is incorrect?
Solution
Exponent Laws
Simplify fully.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Remember
Exponential Equations
Solve for x in the following:
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Exponential Equations
Evaluate ƒ(3).
Solution
ƒ(3) =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Exponential Equations
Give an exact solution to the equation when ƒ(x) = 1024.
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Exponential Equations
Solve the following exponential equations, similar to the steps shown in the example given below.
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
x =
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Solution
x =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Raise both sides by the same exponent
Solution
Video
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Let y = 2x
General Form of Exponential Functions
The following functions all have the same y-intercept.
Solution
The y-intercept for all the functions shown here is (0, 1).
The y-intercept occurs at x = 0
The y-intercept occurs at x = 0
Properties of Exponential Functions
Determine the y-intercept of the following function
Solution
The y-intercept occurs at x = 0
Properties of Exponential Functions
For the function what happens as x → -∞ ?
Solution
See what happens when x → -∞ by plugging in a large negative number (-100000).
As x → -∞, y → 0.
According to the equation , has d = 0.
The exponential function will always approach y → d.
According to the equation , has d = 0.
The exponential function will always approach y → d.
Transformations of Exponential Functions
Which of the following could represent the exponential function graphed below?
Solution

The function has a base 2x so as x → ∞, y → ∞.
The function has a horizontal asymptote located above the x-axis where y = d.
The function has a horizontal asymptote located above the x-axis where y = d.
Which of the following exponential functions does not have a horizontal asymptote located at y = 0?
Solution
has a horizontal asymptote located at y = -1.
The horizontal asymptote is determined by the d value in:
The horizontal asymptote is located at: y = d
The horizontal asymptote is determined by the d value in:
The horizontal asymptote is located at: y = d
Transformations of Exponential Functions
The graph of , is translated 1 unit left and 2 units up, and horizontally compressed by a factor of ½, compared to
Solution
Compared to the parent function:
This is translated 1 unit left...
This is translated 2 units up...
This is horizontally compressed by a factor of ½...
Put that all together into...
This is translated 1 unit left...
This is translated 2 units up...
This is horizontally compressed by a factor of ½...
Put that all together into...
Which of the following exponential functions is horizontally stretched by a factor of 3 and translated 2 units right?
Solution
Horizontally stretched by a factor of 3, k =
Translated 2 units right, (x - c) = (x - 2)
Translated 2 units right, (x - c) = (x - 2)
Transformations of Exponential Functions
The domain and range for the parent exponential function are {x∈ℝ} and {y∈ℝ}.
Solution
The domain is {x∈ℝ}, but the range is {y∈ℝ | y > 0}.
The domain and range are the same for the exponential functions and .
Solution
Although the graph of is increasing while the graph of is decreasing, both graphs exist above the y-axis and have the same range. And both graphs exist for all values of 'x' so both functions have the same domain.
Transformations of Exponential Functions
A horizontal compression by a factor of ½ is the same as a vertical stretch by a factor of 2 as shown in the functions below.
Solution
Point out the points (0, 1), (1, 4), (2, 8) in the function . See that only one of these points is the same (1, 4) - the rest are different.
See that for x = 0 in the point (0, 1) this will be affected by the vertical transformation but not the horizontal transformation...
See that for x = 0 in the point (0, 1) this will be affected by the vertical transformation but not the horizontal transformation...
Transformations of Exponential Functions
Which is the correct range for the exponential function
Solution
Hint
Clear
Info
{y∈ℝ | > }
Incorrect Attempts:
CHECK
Hint Unavailable
The parent function, has a horizontal asymptote at . Since the function is shifted 5 units up, then the new horizontal asymptote is at and the range is above this...
Transformations of Exponential Functions
Determine the domain of the exponential function
Solution
Hint
Clear
Info
{x∈ℝ | > }
Incorrect Attempts:
CHECK
Hint Unavailable
The horizontal asymptote has not been translated, and is still located at y = 0.
Therefore... {x∈ℝ | x > 0}
Therefore... {x∈ℝ | x > 0}
Applications of Exponential Functions
Which of the following exponential functions corresponds to the data in the table below? Solution
| x | ƒ(x) |
| -2 | 4 |
| -1 | 2 |
| 0 | 1 |
| 1 | 0.5 |
| 2 | 0.25 |
Applications of Exponential Functions
A material with a half-life of 1.5 days starts with a mass of 100g and decays over a period of 18 days. Determine the final amount.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
g
Hint Unavailable
Applications of Exponential Functions
A strong cup of coffee contains 200mg of caffeine. Caffeine decreases by 50% in the bloodstream every 5 hours.
 |
Write an equation to model the final amount of caffeine left in the blood stream after t hours.
Solution
If someone drinks a large mug of caffeine at 8pm, what amount of caffeine will remain in their bloodstream at 10:30pm?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
mg
Hint Unavailable
8pm to 10:30pm is 2.5 hours.
Applications of Exponential Functions
A population of bacteria doubles every 96 minutes. If 5 bacteria were incubated in favorable conditions over a period of 1 day, calculate the percent increase.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
%
Hint Unavailable
Total time = 1440 minutes
Percent increase:
Applications of Exponential Functions
A 2048 mg sample of a radioactive isotope is allowed to decay over a total time period, in days, that is 12 more than 4 times the half-life. If 2 mg of the sample remains, determine the half-life.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
days
Hint Unavailable
Let 'x' represent the half-life.
The total time = 4x + 12
The half-life is 2 days.
The total time = 4x + 12 The half-life is 2 days.
Applications of Exponential Functions
Given the function for compounding below, where 'i' is initial amount, 'r' is rate of interest, 't' is time, and 'n' is compounding period:
Which of the following is compounded semiannually (twice per year)?
Solution
'n' represents the compounding period, and for semiannually, n = 2
$100 is invested at a 1.5% quarterly rate for 2 years. Which of the following represents the equation?
Solution
i = $100, r = 1.5, n = 4, t = 2
Sequences and Series
Arithmetic and Geometric Sequences
Which of the following is an arithmetic sequence?
Solution
Terms in an arithmetic sequence are added or subtracted from the preceding term by a common difference.
Which of the following is a geometric sequence?
Solution
Terms in a geometric sequence are multiplied or divided from the preceding term.
Arithmetic and Geometric Sequences
Find the next term in the following patterns:
0.5, 5, 9.5, ___.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Arithmetic sequence. Add 4.5 each time... 0.5, 5, 9.5, 14...
___.
Solution
Video
Arithmetic sequence. Add each time.
General Term Equation
For the arithmetic sequence 5, 3, 1, -1...
The common difference is:
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The following number changes by the constant common difference (-2) from the preceding number.
Write an equation that could model finding the 6th term in the sequence, where n represents the term number.
Solution
The common difference = -2, so d = -2
The sequence starts at 5, so a = 5
Let n represent the term number.
Let tn represent the term.
The sequence starts at 5, so a = 5
Let n represent the term number.
Let tn represent the term.
Using the equation, determine the 23rd term in the sequence.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
n = 23
Find tn
Find tn
Working with Arithmetic Sequences
The 4th term is 46 and the 7th term is 82 in an arithmetic series.
Find the first term (a) and the common difference (d).
Solution
Hint
Clear
Info
d = a =
Incorrect Attempts:
CHECK
Hint Unavailable
t4 = 46
t7 = 82
Elimination: subtract equation 2 - equation 1
Solve for 'a' by substituting d = 12 into equation 1:
t7 = 82
Elimination: subtract equation 2 - equation 1 Solve for 'a' by substituting d = 12 into equation 1:
How many terms are less than 200?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
d = 12
a = 10
tn = 200
Solve for n and round down to the nearest whole number:
Therefore there are 16 terms less than 200.
a = 10
tn = 200
Solve for n and round down to the nearest whole number: Therefore there are 16 terms less than 200.
General Term Equation
Find the 19th term in the sequence below. Reduce fully.
Solution
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Arithmetic sequence.
n = 19.
Find the common difference first:
n = 19.
Find the common difference first:
General Term Equation
To find three numbers between 5 and 53 in an arithmetic sequence, a math student could solve with the following:
Solution
5 + d + d + d = 53
There are 4 spaces between the numbers. Therefore it would be 4d.
The common difference is 12. The numbers are: 5, 17, 29, 41, and 53.
Geometric Sequences
Increasing a number by 22% or 0.22 is the same as multiplying by 1.22.
Solution
e.g) 100 × 1.22 = 122
e.g 2) Increase 93 by 11%: 93 × 1.11 = 103.23
Increasing a number by 3%, four times, = 100 × 1.034
Solution
Decreasing a number by 11% or 0.11 is the same as multiplying by (1 - 0.11).
Solution
An other e.g) Decrease 100 by 5%:
The following sequence is considered geometric: 32, 33, 34, 35, ...
Solution
The common ratio (multiplier) is 3.
Geometric Sequences
For the sequence
Determine the common ratio.
Solution
r =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Write an equation for the sequence, and find the 8th term. Show your work.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
tn is the term
a is the first term
r is the common ratio
n is the term number
a is the first term
r is the common ratio
n is the term number
Geometric Sequences
A math student scored 59% on a recent test. This student wants to get into a good university in two years and has decided to apply themselves, and end up scoring 4% higher on each math test. What percent would the student score on the 12th test?
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
%
Hint Unavailable
a = 59
r = (1 + 0.04) = 1.04
n = 12
The student would score 90.8% on their 12th math test.
r = (1 + 0.04) = 1.04
n = 12
The student would score 90.8% on their 12th math test.
Recursion Formula
Write the first three terms of the sequence: t1 = 3, tn - 1 + 3, n > 1
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Arithmetic Series
Which of the following is an arithmetic series?
Solution
Sequences are separated by commas, series are separated by addition.
Sum of an Arithmetic Series
The sum of the first 21 terms of the series -10 - 4 + 2 + 8 + 14 + ... is 1050
Solution
a = -10
d = +6
n = 21
d = +6
n = 21
Sum of an Arithmetic Series
Arithmetic series: 3 + 10 + 17 + ... 136.
Determine the number of terms in the series.
Solution
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
a = 3
d = 7
tn = 136
Find n.
d = 7
tn = 136
Find n.
Determine the sum of the series.
Solution
Sum =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
n = 20
a = 3
d = 7
Find Sn.
a = 3
d = 7
Find Sn.
Sum of a Geometric Series
The sum of a geometric series is determined with which of the following ?
Solution
Where
- a = first term
- r = common ratio (for geometric)
- n = number of terms in series (or term number)
- Sn = sum of all the terms up to and including n
- tn = value of the term number, n
Where
- a = first term
- r = common ratio (for geometric)
- n = number of terms in series (or term number)
- Sn = sum of all the terms up to and including n
- tn = value of the term number, n
Sum of a Geometric Series
Geometric series: 297 + 99 + 33 + 11 + ...
Determine the number of terms in the series.
Solution
n =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
a = 297
r =
tn =
Find n.
r =
tn =
Find n.
Determine the exact value of the sum of the series. Simplify and reduce fully.
Solution
Sum =
Hint
Clear
Info
━━━━━━
Incorrect Attempts:
CHECK
Hint Unavailable
a = 297
r =
n = 15
Reduce:
r =
n = 15 Reduce:
Sum to Infinity of a Geometric Series
Geometric series can be added to infinity.
The sum to infinity of a geometric series uses the equation below.
Solution
Must use the equation...
The sum to infinity is valid for all common ratios (r).
Solution
Sum to infinity is only possible for common ratios where |r| < 1. Because as the term number approaches infinity, the sum approaches a certain number as the term values approach zero...
A geometric series 25 + 12.5 + 6.25 + 3.125 + ... has the same sum to infinity as a geometric series that starts at 45. Determine the common ratio.
Solution
r =
Hint
Clear
Info
━━
Incorrect Attempts:
CHECK
Hint Unavailable
Set the two sum to infinities equal and solve...
Determine the exact value of M × N if M is the sum to infinity of the geometric series and N is the sum of infinity of Simplify your answer fully.
Solution
Video
M × N =
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Determine common ratio, r for M:
Determine common ratio, r for N:
Multiply the sums to infinity of M × N...
Sum of a Series Word Problem
Determine the total vertical distance travelled by a ball that is dropped from 1 m and loses ⅒ of the height on each bounce.
Solution
d =
Hint
Clear
Info
Incorrect Attempts:
CHECK
m
Hint Unavailable
First find the sum to infinity of the geometric series with a = 1, and r =
...
The total distance travelled is twice the height between two adjacent bounces, except for the fist drop which has just a single 1m height... So the total vertical distance travelled is (S∞ × 2) - 1m.
Financial Mathematics
Compound Interest
A $1000 principal is invested for 4 years at 3% quarterly. Which equation will find the future value?
Solution
FV = future value
R = initial amount
t = time in years
i = rate ÷ 100%
n = compounding periods per year... Quarterly: n = 4
R = initial amount
t = time in years
i = rate ÷ 100%
n = compounding periods per year... Quarterly: n = 4
Compound Interest
Determine the future value of $10,000 invested for 10 years at a 3.1% rate, compounded semiannually.
Solution
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
How much money should be invested now at a 2.5% rate, compounded monthly, to have $100,000 in 5 years?
Solution
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Compound Interest
$10,000 is invested at 1.5% for 3 years.
Determine the future value if the rate is compounded annually.
Solution
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
R = $10,000
i = 0.015
t = 3
n = 1
i = 0.015
t = 3
n = 1
Determine the future value if the rate is compounded daily.
Solution
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
R = $10,000
i = 0.015
t = 3
n = 365
i = 0.015
t = 3
n = 365
Calculate the difference between these future values.
Solution
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Use the future values calculated above.
The difference is $3.49
Annuity
An annuity is the same as a geometric series.
Solution
E.g.) $100 + $100(1.03) + $100(1.03)2 + $100(1.03)3 + ...
In this example the common ratio is 1.03
In this example the common ratio is 1.03
Annuity
An annuity can be calculated when deposits are made on different time intervals than the compounding period.
Solution
The annuity equation is correct for future value:But deposits always must be made in the same intervals as the compounding periods.
Annuity
An annuity refers to either recurring deposits into an account, or recurring withdrawals from an account.
Solution
Regular deposits is calculated with Future Value:
Regular withdrawals is calculated with Present Value:
Annuity (Regular Deposits)
$1,000 is deposited every month into an account paying 3.0% compounded monthly. Calculate the total amount in the annuity after 2 years.
Solution
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
R = $1,000
i = 0.03
n = 12
t = 2
Find future value, FV.
i = 0.03
n = 12
t = 2
Find future value, FV.
Annuity: Initial Amount
To save $10,000 in three years in an account that pays 2% interest, compounded daily, how much should be contributed each day?
Solution
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
FV = $10,000
i = 0.02
n = 365
t = 3 years
Find R.
Therefore $8.86 should be deposited each day.
i = 0.02
n = 365
t = 3 years
Find R. Therefore $8.86 should be deposited each day.
How much interest will have been earned?
Solution
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Annuity: Time
Determine how long it would take for Sarah to save $70,000 if she deposits $500 each month into a savings account at 3% compounded monthly.
Solution
Hint
Clear
Info
Incorrect Attempts:
CHECK
years
Hint Unavailable
Givens:
FV = $70,000
n = 12
i = 3% ÷ 100% = 0.03
t = ?
It would take around 10 years...
FV = $70,000
n = 12
i = 3% ÷ 100% = 0.03
t = ? It would take around 10 years...
Annuity: Present Value (Withdrawal)
Determine the present value of an annuity that would allow someone to withdraw $8,000 per month, from an account with a 3% interest rate, compounded monthly, over a twenty year period. That's a $8,000 cheque every month for twenty years!
Solution
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Annuity, Scholarship
A generous benefactor donates $1 million to provide a scholarship to entrepreneurial, self-starter individuals. This scholarship money is invested by the school authority at 4% per annum, compounded annually. If the fund is to provide a yearly scholarship in perpetuity, without compensating for inflation, determine the amount of each scholarship.
Solution
Video
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Givens:
PV = $1,000,000
i = 0.04
n = 1
t = ∞
R = ?
Each scholarship is worth $40,000!
PV = $1,000,000
i = 0.04
n = 1
t = ∞
R = ? Each scholarship is worth $40,000!
Annuity: Present Value and Future Value Combined
A 12 year-old middle school student wants to electronically deposit $1 each day to give herself some money each day for the first 4 years at university. If she plans on going to university when she turns 18 years-old, calculate the amount of money available each day at university, if her savings account has a 3.5% interest rate, compounded daily.
Solution
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
The future value (FV) of her first 6 years of savings is equal to the present value (PV) of her first 4 years at university.
Givens for deposits for FV:
i = 0.035
n = 365 periods per year
t = 6 years
R = $1
Givens for withdrawals for PV:
i = 0.035
n = 365 periods per year
t = 4 years
R = ?
She will have $1.79 each day for herself in university... (Um, woo yay.)
Givens for deposits for FV:
i = 0.035
n = 365 periods per year
t = 6 years
R = $1 Givens for withdrawals for PV:
i = 0.035
n = 365 periods per year
t = 4 years
R = ? She will have $1.79 each day for herself in university... (Um, woo yay.)
Mortgage
A mortgage is equivalent to the present value of an annuity.
Solution
The mortgage amount is the present value and the deposits are like withdrawals from this present value amount.
The present value formula has two uses...
- For funding retirement starting with $300,000 then PV = $300,000 where R is the monthly payments to yourself
- For a $300,000 mortgage or loan then PV = $300,000 where R is the monthly payments to the lender
- For funding retirement starting with $300,000 then PV = $300,000 where R is the monthly payments to yourself
- For a $300,000 mortgage or loan then PV = $300,000 where R is the monthly payments to the lender
Calculate the monthly payments on a $300,000 mortgage over 25 years at 4% compounded monthly.
Solution
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Givens:
PV = $300,000
t = 25 years
n = 12
i = 0.04
Monthly payments are $1,583.51
PV = $300,000
t = 25 years
n = 12
i = 0.04 Monthly payments are $1,583.51
Calculate the total amount of interest paid.
Solution
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Interest Paid = Sum of Monthly Payments - Present Value of Loan
That is a lot of interest to pay!
Partial Loans
A car loan for 48 months at 2.9% compounded monthly, costs the driver $500 per month.
If the driver put $3540 down on the car, calculate the original price of the car.
Solution
Video
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Loans are present value (PV)...
PV = Original Price - Down Payment = OP - $3540
The value of the loan was $22,634.51 and the original selling price of the car including the down payment was $26,174.51
PV = Original Price - Down Payment = OP - $3540 The value of the loan was $22,634.51 and the original selling price of the car including the down payment was $26,174.51
Calculate the interest paid on the loan.
Solution
Video
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Interest Paid = Sum of Monthly Payments - Present Value of Loan
The interest paid to use the car for 48 months is $1,365.49
(Aside: part of this can be written off on taxes when the car is used only for your business)
(Aside: part of this can be written off on taxes when the car is used only for your business)
Mortgage Precision of Different Compound Periods
A mortgage on a home is $250,000 at 3.5% compounded semiannually, with a 25 year amortization period. Determine the monthly payments.
Solution
$
Hint
Clear
Info
Incorrect Attempts:
CHECK
Hint Unavailable
Mortgages typically have semi-annual compounding, while the payments are monthly. This is an exception that is allowed.
First determine the interest rate on a monthly basis (for monthly payments). A 3.5% rate is 1.75% every 6 months. Convert this rate to a monthly rate after 6 months:
n = 12 (monthly), t = 25, Solve for R...
We have determined i = 0.0028956 so we use a slightly different equation...
First determine the interest rate on a monthly basis (for monthly payments). A 3.5% rate is 1.75% every 6 months. Convert this rate to a monthly rate after 6 months: n = 12 (monthly), t = 25, Solve for R...
We have determined i = 0.0028956 so we use a slightly different equation...
